主成分分析（PCA）によるプロ野球選手の打者の分類

概要

野球選手の打者にはいろいろなタイプがいるといわれていて、

• ボールを遠くに飛ばせてホームランを多く打つけど安打が少ない
• ボールを遠くに飛ばせないけど良くヒットを打っていて安打が多い
• ホームランもヒットもそこそこだけど足が速くて二塁打や盗塁が多い
• ホームランもヒットも盗塁も多い万能型

などなど。このようにバッティング（走力も含めて）にはいろいろなタイプがいるといわれています。そこで2018年のプロ野球のデータから主成分分析を用いて打者をタイプ別に分類したいと思います！！！！

環境

• Windows10
• google Colaboratory
• google ドライブ

データはgoogle ドライブに保存しています

主成分分析とは

主成分分析は多次元の量的なデータから、情報をできるだけ残すようにして、より少ない指標や合成変数（複数の変数が合体したもの）に要約する手法です。
例えば、ホームランと打点から「パワー系」という指標を導くなどです。

データ

日本プロ野球の2018年の規定打席に達したセリーグとパリーグの60選手

分析には以下のようなデータセットを用いました

選手名	安打	二塁打	三塁打	本塁打	打点	三振	四球	盗塁	盗塁死
ビシエド	178	26	1	26	99	61	51	3	4
坂本　勇人	152	27	2	18	67	83	61	9	5
平田　良介	162	26	5	9	55	69	67	8	7
青木　宣親	162	37	3	10	67	48	51	3	4
アルモンテ	160	37	0	15	77	95	44	1	1

分析

必要なライブラリをインポート

import os
import pandas as pd
import numpy as np
import scipy.stats as stats

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
%config InlineBackend.figure_formats = {'png', 'retina'}
sns.set(font = "IPAGothic")

from IPython.display import display, Image

pd.options.display.max_columns = 500

データの取り込み

googleドライブへマウント

from google.colab import drive
drive.mount('/content/drive')

ディレクトリの移動

cd drive/My\ Drive/********* #データが保存されているディレクトリまで移動します

csvの読み込み

b_data = pd.read_csv('batting_data.csv')

# 選手名を抜く
b_data_select = b_data.iloc[:, 1:10]
b_data_select

標準化

主成分分析を行う際は標準化するのが一般的なようです。標準化のメリットは「スケールの異なる変量を扱う時に比較しやすくする」というものがあります。

sc = StandardScaler()
b_data_std = pd.DataFrame(sc.fit_transform(b_data_select))

b_data_std.head()

	0	1	2	3	4	5	6	7	8
0	1.757838	0.269390	-0.633609	0.724544	1.287217	-1.141774	-0.188878	-0.581232	0.079771
1	0.644017	0.415006	-0.288004	0.035869	-0.088872	-0.230013	0.257290	-0.037742	0.345675
2	1.072410	0.269390	0.748810	-0.738892	-0.604906	-0.810225	0.524991	-0.128324	0.877482
3	1.072410	1.871166	0.057601	-0.652807	-0.088872	-1.680542	-0.188878	-0.581232	0.079771
4	0.986731	1.871166	-0.979213	-0.222385	0.341156	0.267312	-0.501196	-0.762396	-0.717940

次元を決定及び、次元の圧縮

主成分分析は多次元の量的なデータを、情報をできるだけ残すようにして、より少ない指標や合成変数（複数の変数が合体したもの）に圧縮する手法なので、いくつの合成変数にするかを決める必要があります。
今回は3次元に圧縮したいと思います。野球では「パワーヒッター」と「アベレージヒッター」といわれるタイプがあり、今回はそれにプラスしてどちらでもないタイプ（例えば、ホームランも安打数も平均的だけど、足は速いみたいなタイプ）の選手もいると思い、3次元に圧縮したいと思います。

# 3次元に圧縮するPCAインスタンスを作成
pca = PCA(n_components = 3, random_state = 0) # n_components()の部分で合成変数の数を決めます
# b_data_stdデータをPCAで次元圧縮
X_pca = pca.fit_transform(b_data_std)

固有ベクトルを算出

固有ベクトルとは主成分に対して元の変数がどの程度影響を与えているかの値です。

pd.DataFrame(pca.components_)

	0	1	2	3	4	5	6	7	8
0	0.236712	0.313554	-0.292690	0.481108	0.510233	0.229937	0.287450	-0.251096	-0.263881
1	0.411177	0.182261	0.392873	0.028260	0.055126	0.260939	0.354493	0.473114	0.471101
2	0.445215	0.563800	0.037510	-0.281719	-0.098115	-0.600219	-0.038400	-0.147453	-0.100175

データフレームにして見ましたが、これだと判断するのが難しいので、各成分ごとに可視化して解釈して見たいと思います。

各成分の可視化と解釈

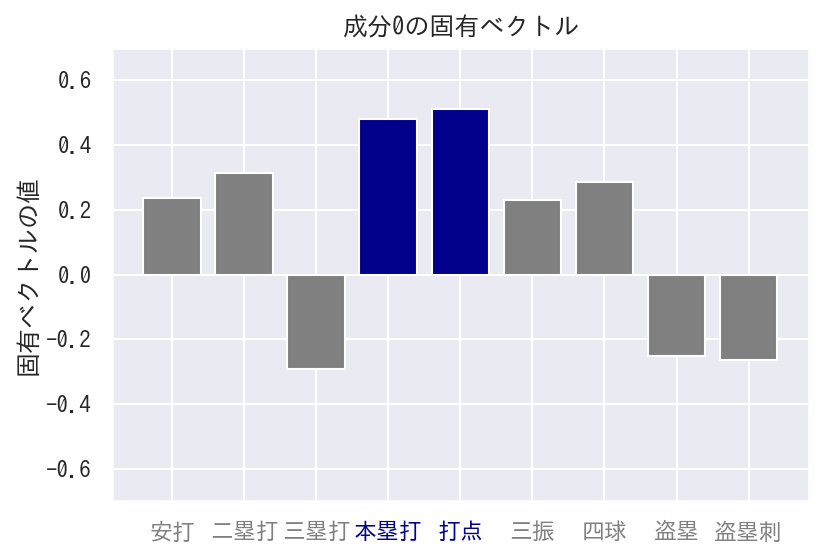
成分0

colorlist= ['grey', 'grey', 'grey', 'darkblue', 'darkblue', 'grey', 'grey', 'grey', 'grey']

plt.figure(1)     
ax = plt.subplot(111)
ax.bar(b_data_select.columns, pca.components_[0], color=colorlist)
ax.set_xticks(b_data_select.columns)
ax.set_xticklabels(b_data_select.columns, rotation = 270)
ax.set_title('成分0の固有ベクトル')
ax.set_ylabel('固有ベクトルの値')
plt.ylim([-0.7, 0.7])
plt.xticks(rotation = '0')

for xtick, color in zip(ax.get_xticklabels(), colorlist):
    xtick.set_color(color)

成分0のグラフを確認すると、特に本塁打と打点の固有ベクトルの値が大きくなっていますね。つまり、成分0では、これらの影響が大きいといえます。
本塁打と打点の特徴のある選手となれば、やはり「パワーヒッター」ではないでしょうか。成分0は「パワーヒッター」とします。

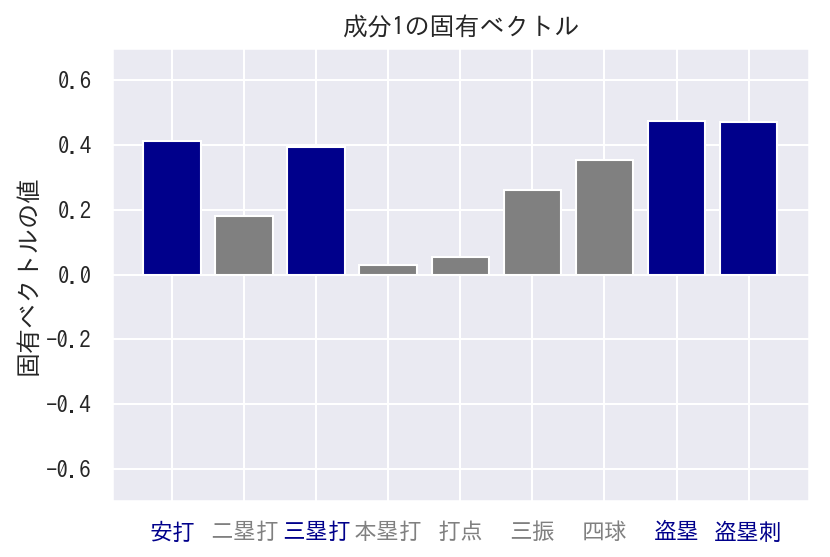
成分1

colorlist = ('darkblue', 'grey', 'darkblue', 'grey', 'grey', 'grey', 'grey', 'darkblue', 'darkblue')

plt.figure(1)     
ax = plt.subplot(111)
ax.bar(b_data_select.columns, pca.components_[1], color = colorlist)
ax.set_xticks(b_data_select.columns)
ax.set_xticklabels(b_data_select.columns, rotation = 270)
ax.set_title('成分1の固有ベクトル')
ax.set_ylabel('固有ベクトルの値')
plt.ylim([-0.7, 0.7])
plt.xticks(rotation = '0')

for xtick, color in zip(ax.get_xticklabels(), colorlist):
    xtick.set_color(color)

成分1のグラフを確認すると、特に安打、三塁打、盗塁、盗塁死の固有ベクトルの値が大きくなっています。
分類するのにここは少し迷いますが、「良く打つ上に足が速い」ということで成分1を「リードオフマン」とします！

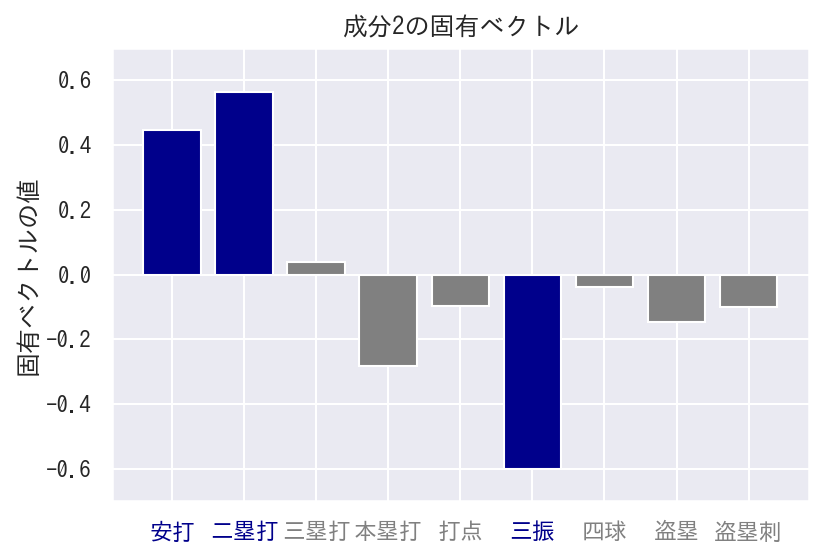
成分2

colorlist= ('darkblue', 'darkblue', 'grey', 'grey', 'grey', 'darkblue', 'grey', 'grey', 'grey')


plt.figure(1)     
ax = plt.subplot(111)
ax.bar(b_data_select.columns, pca.components_[2], color = colorlist)
ax.set_xticks(b_data_select.columns)
ax.set_xticklabels(b_data_select.columns, rotation = 270)
ax.set_title('成分2の固有ベクトル')
ax.set_ylabel('固有ベクトルの値')


plt.ylim([-0.7, 0.7])
plt.xticks(rotation = '0')

for xtick, color in zip(ax.get_xticklabels(), colorlist):
    xtick.set_color(color)

成分1のグラフを確認すると、安打と二塁打の成分が大きく、三振はマイナスに大きくなっています。
良く打ち、三振が少ないとなるとこれぞ「アベレージヒッター」といえますね。成分2はアベレージヒッターとします。

寄与率

主成分分析は多次元の量的なデータを、情報をできるだけ残すようにして、より少ない指標や合成変数（複数の変数が合体したもの）に要約する手法です。そうです。どれだけの情報が残ったのかを確認する必要があります。その判断をするのが、寄与率です。各成分ごとに寄与率があり、すべての成分（今回は全部で3）を足したものが累積寄与率といわれるものです。この累積寄与率が0.7から0.8くらいあれば良しとされているようです。逆に累積寄与率が少なすぎると情報を多く失っていることになり、分析をするには堪えないものになってしまいます。
ということで、今回の累積寄与率を確認してみます。

print('各主成分の寄与率:', pca.explained_variance_ratio_)
print('寄与率の累積:', sum(pca.explained_variance_ratio_))

各主成分の寄与率: [0.35970777 0.26324623 0.14976546]
寄与率の累積: 0.7727194534681444

見事、0.77ということで、情報を残したまま主成分分析ができました！

主成分得点の算出

それでは、各選手の主成分得点を算出して、各選手をタイプ別に割り振っていたいと思います！

result = pd.DataFrame(X_pca)
result.columns = ['成分0', '成分1','成分2']
result['選手タイプ'] = result.idxmax(axis = 1)
result['name'] = b_data['選手名']

type_mapping = {'成分0': '成分0_パワーヒッター', '成分1': '成分1_リードオフマン', '成分2': '成分2_アベレージヒッター'}

result['選手タイプ'] = result['選手タイプ'].map(type_mapping)
result = pd.concat([result, b_data_select], axis = 1 )
result.head()

成分0|成分1|成分2|選手タイプ|name|安打|二塁打|三塁打|本塁打|打点|三振|四球|盗塁|盗塁刺
|:-----------|:-----------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|
|1.499452|0.012090|1.350596|成分0_パワーヒッター|ビシエド|178|26|1|26|99|61|51|3|4
|0.278110|0.399589|0.607633|成分2_アベレージヒッター|坂本　勇人|152|27|2|18|67|83|61|9|5
|-0.779698|1.057367|1.322105|成分2_アベレージヒッター|平田　良介|162|26|5|9|55|69|67|8|7
|0.148472|0.038389|2.820863|成分2_アベレージヒッター|青木　宣親|162|37|3|10|67|48|51|3|4
|1.472248|-0.432263|1.529855|成分2_アベレージヒッター|アルモンテ|160|37|0|15|77|95|44|1|1

主成分得点の一番高いものを各選手のタイプとして割り振っていきます。例えばビシエド選手でいえば、成分0、成分1、成分2がそれぞれ「1.499452」、「0.012090」、「1.350596」となっており、この中で最も値の高いのは成分0となり、成分0はパワーヒッターの特徴があるため、ビシエド選手は「パワーヒッター」に分類されます。

これで各選手にタイプ別の分類が終わりました！！
今回の主成分分析による分類が主観とあっているか見てみたいと思います！

パワーヒッター

result.query('選手タイプ == "成分0_パワーヒッター"').sort_values(by = '成分0', ascending = False).head(10)

成分0|成分1|成分2|選手タイプ|name|安打|二塁打|三塁打|本塁打|打点|三振|四球|盗塁|盗塁刺
|:-----------|:-----------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|
|4.119948|0.399654|-1.756427|成分0_パワーヒッター|山川　穂高|152|24|1|47|124|138|88|0|0
|3.475278|-0.104278|-1.623849|成分0_パワーヒッター|バレンティン|138|22|0|38|131|121|85|1|1
|3.233612|0.468008|0.015143|成分0_パワーヒッター|浅村　栄斗|175|27|0|32|127|105|68|4|2
|2.931323|-0.033810|0.018800|成分0_パワーヒッター|筒香　嘉智|146|33|1|38|89|107|80|0|0
|2.865723|0.253480|-0.456502|成分0_パワーヒッター|岡本　和真|167|26|0|33|100|120|72|2|1
|2.536532|2.034039|-2.279998|成分0_パワーヒッター|丸　佳浩|132|22|0|39|97|130|130|10|10
|2.268064|0.770411|-0.484774|成分0_パワーヒッター|鈴木　誠也|135|32|2|30|94|116|88|4|4
|2.048710|0.229483|1.799239|成分0_パワーヒッター|吉田　正尚|165|37|2|26|86|74|69|3|1
|1.998534|-0.981408|0.793577|成分0_パワーヒッター|中田　翔|143|32|0|25|106|81|43|0|1
|1.828866|-0.454304|-0.338458|成分0_パワーヒッター|井上　晴哉|139|26|2|24|99|106|63|1|0

山川選手、浅村選手、中田選手などいかにもな選手が綺麗にパワーヒッターに分類されました！皆さんの感覚ではいかがでしょうか？僕としてはかなり良い感じに分類できたと思います！！

リードオフマン

result.query('選手タイプ == "成分1_リードオフマン"').sort_values(by = '成分1', ascending = False).head(10)

成分0|成分1|成分2|選手タイプ|name|安打|二塁打|三塁打|本塁打|打点|三振|四球|盗塁|盗塁刺
|:-----------|:-----------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|
|-1.972976|3.789957|-1.174956|成分1_リードオフマン|田中　広輔|150|19|10|10|60|118|75|32|13
|1.074528|3.617441|1.717807|成分1_リードオフマン|秋山　翔吾|195|39|8|24|82|96|77|15|10
|-1.560951|3.296507|0.307986|成分1_リードオフマン|中村　奨吾|157|30|3|8|57|94|60|39|15
|1.934455|3.075147|-0.619577|成分1_リードオフマン|山田　哲人|165|30|4|34|89|119|106|33|4
|-1.871698|2.957498|0.488734|成分1_リードオフマン|源田　壮亮|165|27|9|4|57|101|48|34|8
|-1.033007|2.756313|-0.297568|成分1_リードオフマン|西川　遥輝|147|25|6|10|48|103|96|44|3
|1.540711|2.269514|-0.249914|成分1_リードオフマン|柳田　悠岐|167|29|5|36|102|105|62|21|7
|-1.050262|1.870962|-0.271466|成分1_リードオフマン|上林　誠知|149|26|14|22|62|117|30|13|4
|-1.892742|1.762230|0.410165|成分1_リードオフマン|大島　洋平|161|20|7|7|57|80|47|21|9
|-0.826188|1.239028|-0.814193|成分1_リードオフマン|外崎　修汰|130|24|3|18|67|102|47|25|9

さて、続いてリードオフマンに分類される選手たちです。田中選手、秋山選手、西川選手、大島選手などリードオフマンらしい選手たちが分類されたのではないでしょうか。なかには、山田選手、柳田選手のように万能型の選手も混ざっていますね。両選手はホームランも打つためパワーヒッターの主成分得点も高い値を示しています。

アベレージヒッター

result.query('選手タイプ == "成分2_アベレージヒッター"').sort_values(by = '成分2', ascending = False).head(10)

成分0|成分1|成分2|選手タイプ|name|安打|二塁打|三塁打|本塁打|打点|三振|四球|盗塁|盗塁刺
|:-----------|:-----------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|:------------|
|0.148472|0.038389|2.820863|成分2_アベレージヒッター|青木　宣親|162|37|3|10|67|48|51|3|4
|1.433628|-1.033999|2.573731|成分2_アベレージヒッター|宮﨑　敏郎|175|34|0|28|71|45|38|0|0
|-0.875345|0.640445|1.617678|成分2_アベレージヒッター|糸原　健斗|152|29|4|1|35|73|86|6|4
|1.472248|-0.432263|1.529855|成分2_アベレージヒッター|アルモンテ|160|37|0|15|77|95|44|1|1
|-1.520669|0.812603|1.379947|成分2_アベレージヒッター|坂口　智隆|161|22|4|3|37|60|75|9|7
|0.306141|-0.835488|1.327918|成分2_アベレージヒッター|中村　晃|148|28|1|14|57|68|60|1|1
|-0.779698|1.057367|1.322105|成分2_アベレージヒッター|平田　良介|162|26|5|9|55|69|67|8|7
|-1.581069|-0.304457|1.266761|成分2_アベレージヒッター|鈴木　大地|127|27|6|8|49|55|44|8|4
|-0.318830|-1.842122|1.128704|成分2_アベレージヒッター|松山　竜平|120|25|2|12|74|46|42|2|0
|-1.692304|-1.282355|0.964900|成分2_アベレージヒッター|銀次|136|16|5|5|48|47|48|1|1

最後にアベレージヒッターに分類される選手たちです。青木選手や糸原選手、銀二選手など良く打つうえに三振が少ない選手が並びました。三振の数はみんな2桁です（この表に載っていないアベレージヒッターに分類される選手全員が三振の数が2桁でした）！まさにアベレージヒッターが綺麗に分類されたのではないでしょうか！

まとめ

今回は主成分分析を用いて、昨年のプロ野球のデータから打者のタイプを3つに分類しました。その結果、ホームランが多く打点が多い「パワーヒッター」、良く打ち盗塁も多い「リードオフマン」、良く打ち三振の少ない「アベレージヒッター」の3つに分類されました。個人的には良い感じに分類できたのではないかと思います。