まずは例題を見てみよう!
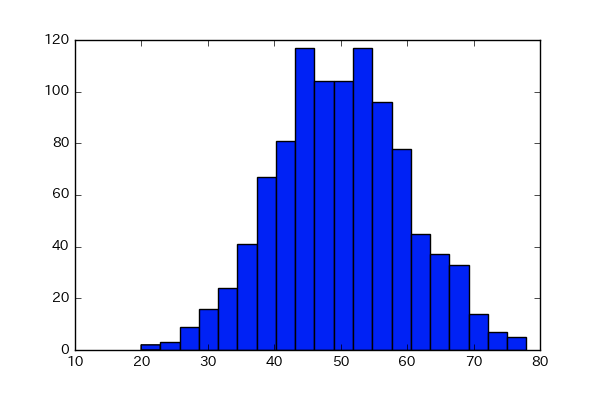
例題1:たとえば、1000人が受けた数学のテストがあり、平均が50、標準偏差(std)が10だったとして、それをヒストグラムに出します。
import numpy as np
import matplotlib.pyplot as plt
# 平均 50, 標準偏差 10 の正規乱数を1,000件生成
x = np.random.normal(50, 10, 1000)
# ヒストグラムを出力
plt.hist(x, bins=20)
filename="hist2.png"
plt.savefig(filename)
plt.show()
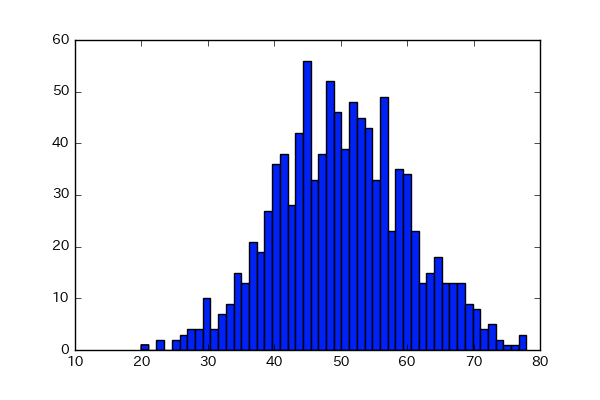
plt.hist(x, bins=50)
filename="hist.png"
plt.savefig(filename)
plt.show()
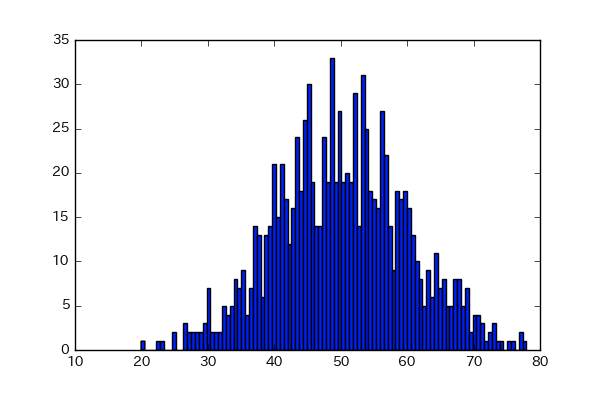
plt.hist(x, bins=100)
filename="hist.png"
plt.savefig(filename)
plt.show()
このヒストグラムの幅を短くしていくと、曲線に近くなります!
このように、階級の幅を最小まで短くした曲線の式を、統計では確率密度関数と呼びます!
ポイント
確率密度関数のグラフには、3つのポイントがあります。
それは、
1つ目は平均を中心に、左右が対象であるという特徴
コメントで
ポアソン分布のように非対称な分布関数も存在します
ということをおしえて頂きました!なので、すべての分布が平均を中心に左右対称とは異なるようです。@SatoshiTerasaki ありがとうございますm(__)m
2つ目は平均(avg,mean,μなどが平均です!)と標準偏差(std, σ)の影響を受けるという特徴
3つ目は、あとで証明も行いますが、**確率==割合(==面積)**という特徴
4つ目は(分かりづらかったので付け足すと、)確率密度関数とは、正規分布やカイ二乗分布...等の総称である!
という点です!
今回は正規分布(ガウス分布)、標準正規分布という2つの分布に触れていきます!
正規分布と標準正規分布
**正規分布(normal distribution)**の公式を覚えていきます!
正規分布の公式
{\displaystyle f(x)={\frac {1}{\sqrt {2\pi \sigma^{2}}}}\exp \!\left(-{\frac {(x-\mu )^{2}}{2\sigma^{2}}}\right)\quad (x\in \mathbb {R} )}
誰もが【わかりづらい!!!】と感じるはずなので、日本語化して、記号の説明もします!
記号の説明!
①:exp = ネイピア数!(定数で、πのようなものだと覚えるだけで大丈夫です!)
②: σの2乗 = 分散σの2乗、標準偏差です!
(統計学① 基準値、標準偏差をわかりやすく説明します!で説明しているので、参考にしてください(^^)!)
③:μ = 平均(母平均)です!
(統計学① 基準値、標準偏差をわかりやすく説明します!で説明しているので、参考にしてください!)
これをもとに、さっきの式を和訳してみます!
まずは、正規分布の公式です!
{\displaystyle f(x)={\frac {1}{\sqrt {2\pi \times 標準偏差}}}e \!\left(-{\frac {(x-平均 )^{2}}{2\times 標準偏差}}\right)}
統計学では、**【xは、平均が~~~で標準偏差がxxxの正規分布に従う】**と表せるようです!
例題1の問題であれば、【xは、平均が50で標準偏差が10の正規分布に従う】と表せます!
それでは、matplotlib,Scipyを使って表示してみましょう!
僕はAnacondaを導入しているので、jupyternotebookを利用していきます。
# numpy,scipy.statsからnorm,math,matplotlib.pyplotをインポート!
import numpy as np
from scipy.stats import norm
import math
import matplotlib.pyplot as plt
# 0から100まで、0.01間隔で入ったリストXを作る!
X = np.arange(0,100,0.1)
# 確率密度関数にX,平均50、標準偏差20を代入
Y = norm.pdf(X,50,20)
# x,yを引数にして、関数の色をr(red)に指定!カラーコードでも大丈夫です!
plt.plot(X,Y,color='r')
plt.show()
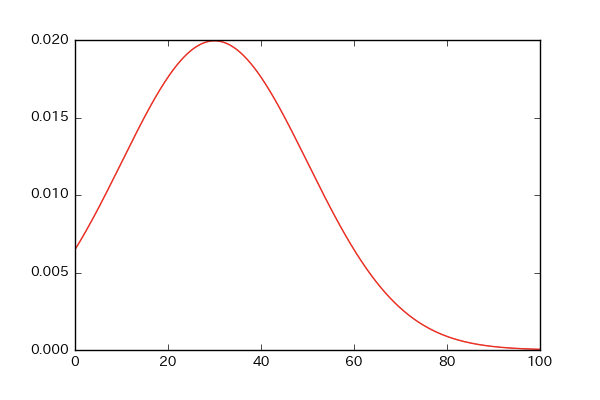
平均が30,標準偏差が20の正規分布!
# numpy,scipy.statsからnorm,math,matplotlib.pyplotをインポート!
import numpy as np
from scipy.stats import norm
import math
import matplotlib.pyplot as plt
X = np.arange(0,100,0.1)
Y = norm.pdf(X,30,20)
plt.plot(X,Y,color='r')
plt.show()
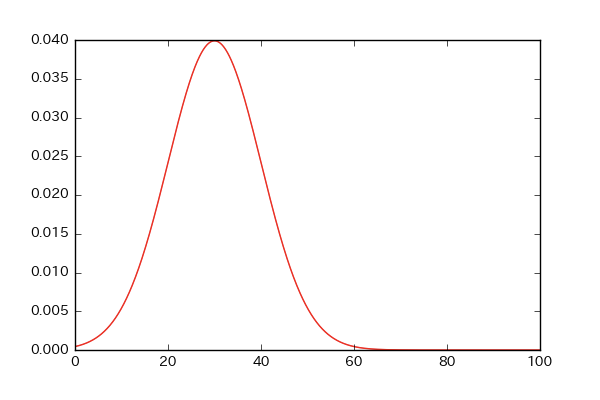
平均が30、標準偏差が10の正規分布!
# numpy,scipy.statsからnorm,math,matplotlib.pyplotをインポート!
import numpy as np
from scipy.stats import norm
import math
import matplotlib.pyplot as plt
X = np.arange(0,100,0.1)
Y = norm.pdf(X,30,10)
plt.plot(X,Y,color='r')
plt.show()
正規分布のPOINT!
一番最初に書きましたが、平均と標準偏差に影響を受けているのが、お分かりになるでしょうか!
このグラフを書いていて正直わからなかったこと。
ヒストグラムとこの関数を同時にplotできない!
誰か方法を知っている方いましたら教えてください!m(__)m
標準正規分布
次に、標準正規分布の公式です!
まずは公式!
f(x)={\frac {1}{{\sqrt {2\pi }}}}e \!\left(-{\frac {x^{2}}{2}}\right)
標準正規分布と、正規分布の違いは結局何なのか!!!
先程あげた標準正規分布の式は、【xは、平均が0で標準偏差が1の正規分布に従う】場合なのです!
計算してみましょう!
\begin{align}
f(x)&={\frac {1}{\sqrt {2\pi \times 標準偏差}}}e \!\left(-{\frac {(x-平均 )^{2}}{2\times 標準偏差}}\right)\\
&=\frac{1}{\sqrt{2 \pi \times 1 }}e \!\left(-{\frac {(x-0 )^{2}}{2\times 1}}\right)\\
&=\frac{1}{\sqrt{2 \pi }}e \!\left(-{\frac {x^{2}}{2}}\right)\\
\end{align}
先程の式と同じになりましたね!
f(x)={\frac {1}{{\sqrt {2\pi }}}}e \!\left(-{\frac {x^{2}}{2}}\right)
標準正規分布のPOINT!
この場合、先程あげた【xは、平均が0で標準偏差が1の正規分布に従う】ではなく、
**【xは標準正規分布にしたがう!】**と表現されます!
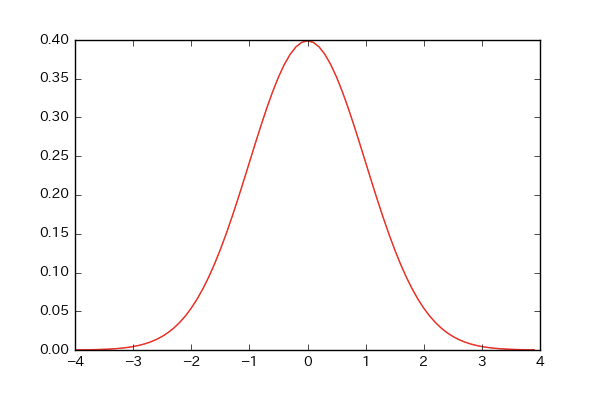
グラフにしてみましょう!
# numpy,scipy.statsからnorm,math,matplotlib.pyplotをインポート!
import numpy as np
from scipy.stats import norm
import math
import matplotlib.pyplot as plt
# Xを0.1つづ-4から4の間の数字を取り出したリストにする。
X = np.arange(-4,4,0.1)
# リストになっているか確認!(^^)
# >>> print(X)
# [ -4.00000000e+00 -3.90000000e+00 -3.80000000e+00 -3.70000000e+00
-3.60000000e+00 -3.50000000e+00 -3.40000000e+00 -3.30000000e+00
-3.20000000e+00 -3.10000000e+00 -3.00000000e+00 -2.90000000e+00
-2.80000000e+00 -2.70000000e+00 -2.60000000e+00 -2.50000000e+00
-2.40000000e+00 -2.30000000e+00 -2.20000000e+00 -2.10000000e+00
-2.00000000e+00 -1.90000000e+00 -1.80000000e+00 -1.70000000e+00
-1.60000000e+00 -1.50000000e+00 -1.40000000e+00 -1.30000000e+00
-1.20000000e+00 -1.10000000e+00 -1.00000000e+00 -9.00000000e-01
-8.00000000e-01 -7.00000000e-01 -6.00000000e-01 -5.00000000e-01
-4.00000000e-01 -3.00000000e-01 -2.00000000e-01 -1.00000000e-01
3.55271368e-15 1.00000000e-01 2.00000000e-01 3.00000000e-01
4.00000000e-01 5.00000000e-01 6.00000000e-01 7.00000000e-01
8.00000000e-01 9.00000000e-01 1.00000000e+00 1.10000000e+00
1.20000000e+00 1.30000000e+00 1.40000000e+00 1.50000000e+00
1.60000000e+00 1.70000000e+00 1.80000000e+00 1.90000000e+00
2.00000000e+00 2.10000000e+00 2.20000000e+00 2.30000000e+00
2.40000000e+00 2.50000000e+00 2.60000000e+00 2.70000000e+00
2.80000000e+00 2.90000000e+00 3.00000000e+00 3.10000000e+00
3.20000000e+00 3.30000000e+00 3.40000000e+00 3.50000000e+00
3.60000000e+00 3.70000000e+00 3.80000000e+00 3.90000000e+00]
# 平均が0,標準偏差が1の確率密度関数をつくる!
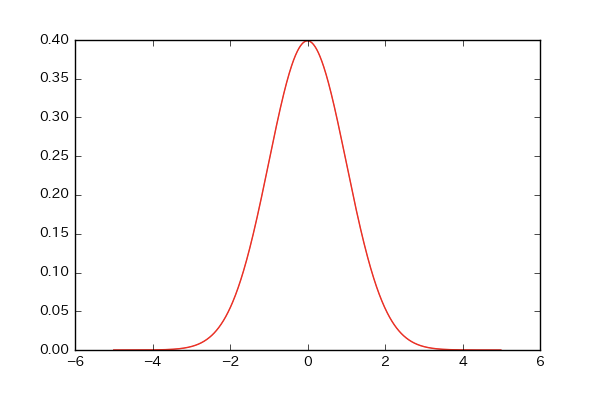
Y = norm.pdf(X,0,1)
plt.plot(X,Y,color='r')
plt.show()
このような形のようです!
この標準正規分布は、結局何に使うのか!
わかりやすくいうと、基準値を元に、標準正規分布表を使って、ある部分の面積(確率)を求めることが出来るのです!
わかりづらいと思うんですが、さっきの例題1であれば、64点以上取れる人がどれくらいいる確率があるか知ることが出来ます!
というわけで、早速問題を解いて行きます!
例題2:1000人が受けた数学のテストがあり、平均が50、標準偏差(std)が10でした。64点以上を取った人が全体のどれくらいいたか確率を求めなさい!
問1:64点を基準化して、基準値Zを求めなさい!
詳しいやり方は統計学① 基準値、標準偏差をわかりやすく説明します!にて!
64点の基準値(z) = \frac{64-50}{10} = 1.40
問2:標準正規分布表を使って、64点以上をとった人がどれだけいたか求めなさい!
標準正規分布表はこちらです!
どうやら、1.40を標準正規分布表で確認すると、0.4192でした!
つまり、1.40以上の面積は0.4192で、64点以上を取った人は41.92パーセントです!
このようなことを求めることが出来るのが標準正規分布です!
ちなみに、今回のようなz以上を求める場合は**生存関数(sf (Survival function) )**と言うものを使い、64点以下の人数を求める場合は、**累積分布関数(cdf (Cumulative density function))**で求めます!
標準正規分布のポイント!!
1:確率==割合==面積である!
確率==割合(==面積)という特徴
がある点に触れましたが、まさにここでした!
2:標準正規分布の面積は1!
※そのため、下記のような計算もできます!
1 - sf = cdf
1 - cdf = sf
参考:【scipy.stats - scipyの統計関数群のAPI】
おわりに
わかりづらい点、誤っている点もあるかと思いますが、その際はおしえていただけますと幸いです!
最後迄読んでいただきありがとうございました(^^)!