TL;DR

最尤推定＝尤度（パラメータを固定したときに観測値が得られる確率）を最大にするパラメータを推定値とするやり方
MAP推定＝尤度に事前確率（観測値を観測する前にパラメータはこれぐらいの値だろうという思い込み）を掛けた事後確率を最大にするパラメータを推定値とするやり方

1.2 確率理論

観測データが有限であることや観測ノイズがあることから、不確かさ (uncertainty) が存在
不確かさを定量評価するための数学的道具 ⇒ 確率理論
不確かさを確率として定量的に評価できると、最適な「意思決定」を導き出せるようになる（詳しくは後で出てくる決定理論で。AかBかを判定する2クラス問題の場合、Aが誤りである確率とBが誤りである確率を求め、誤り確率を最小化するような意思決定法がある）

言葉の整理

真面目に考えだすとややこしいが。。。
- 確率変数は以下では$X$とか$Y$と大文字で表される。変数なので、いろいろな値を取るのだが、どんな値をとるかが確率的に決まるもの
(例：箱を表す確率変数$X$は0.4の確率で赤、0.6の確率で青)
- 確率変数が具体的にとる値は$x$とか$y$とか小文字で表される
- $p(大文字X)$はX（確率変数）がとる値$x$の確率を計算する関数。確率分布ともいう。
例：

p(X) = \left\{
\begin{array}{ll}
0.4 & (x = 赤) \\
0.6 & (x = 青)
\end{array}
\right.

$p(小文字x)$は値が$x$となるときの確率値でスカラー。
例： $p(x=赤) = 0.6$
ただしこれ以降、小文字も大文字も明確に区別されずに表記される場合があるので要注意。
結局、関数なのか確率値を指しているかは空気を読まないといけない

sum ruleとproduct rule

sum rule
同時確率 $p(X, Y)$ において、片方の変数が取りえる値すべてに関して足し合わせる (周辺化する = marginalize) とその変数が消去でき、周辺確率 $p(X)$ が得られる

$$
p(X) = \sum_Y p(X,Y) \tag{1.10}
$$

直観的なイメージを掴む例：$X$が性別(男, 女), $Y$が使っているケータイのキャリア¹(D社, A社, S社)としよう。すると、

\begin{align}
p(X=男) &= p(D社を使っている男) + p(A社の男) + p(S社の男) \\
        &= p(男, D) + p(男, A) + p(男, S) \\
        &= \Sigma_{キャリアに関して} p(男, キャリア)
\end{align}

今までの例では$Y$が離散値だったので$\Sigma$で足し合わせればよかった。 $Y$が身長のように連続値になったときの、$p(X=男)$を求めるときは積分に変わって

\begin{align}
p(X=男) &= \int_{y=あらゆる身長} p(男, y) dy
\end{align}

となる。

product rule
条件（＝前提）$X$を置いたときの確率を条件付き確率 $p(Y | X) $という。 (例：箱$X$が赤だったとという条件（＝前提）のときに、その中に入っている果物$Y$の確率）条件付き確率 $p(Y | X) $と条件$X$の積は同時確率$p(X, Y)$になる

$$
p(X, Y) = p(Y | X) p(X) \tag{1.11}
$$

直観的なイメージを掴む例：またまた$X$が性別(男, 女), $Y$が使っているケータイのキャリア(D社, A社, S社)としよう。すると、男かつD社を使っている確率は男の中でD社を使っている確率に男である確率を掛けたものになる。

\begin{align}
p(X=男, Y=D社) &= p(男の中でD社を使っている) \times p(男) = p(D|男) p(男)
\end{align}

ベイズの定理

またまた$X$が性別(男, 女), $Y$が使っているケータイのキャリア(D社, A社, S社)としよう。ある人が「男かつD社ユーザの確率」と「D社ユーザかつ男な確率」って全く同じことを指している。つまり、数学的には$p(X, Y) = p(Y, X)$。
$p(X, Y) = p(Y, X)$であることとsum ruleより
$$
p(Y | X) p(X) = p(Y, X) = p(X, Y) = p(X | Y) p(Y)
$$
両辺を$p(Y)$で割ると下式のベイズの定理が導出できる
$$
p(Y | X) = \frac{p(X|Y) p(Y)} {p(X)} \tag{1.12}
$$
ベイズの定理により、事前確率( prior probability) と事後確率 (posterior probability) という重要な概念が得られる。
テキストの箱(B)と果物(F)を例とする。式(1.12)から$p(B|F)$が$p(F|B), p(B)$から計算できることを頭にいれておき、
目の前にある箱$B$が$B=red$である確率を求めたいとする。
- 事前確率 : $F$について観測する前（事前）に知っている情報である$p(B)$。
  $p(B)$はあらかじめ赤箱と青箱を何度も観測し、出た割合の比で与える（テキストでは赤40%, 青60%）場合もあるし、観測もできず全く$p(B)$に関して情報がない場合は50%, 50%としておくこともある。
- 事後確率 : $F$が何であったかを観測した後（事後）に求まる条件付き確率 $p(B|F)$。
  事前確率が赤40%, 青60%だとしても観測した$F$がオレンジだった場合、目の前にある箱$B$は箱の中に占めるオレンジの割合が大きい赤箱である可能性が高くなる（直観と一致している）。定量的にどれぐらい確率が高くなったかを$p(B), p(F|B)$から求められる。
独立：$p(X,Y) = p(X) p(Y)$のとき、$X$と$Y$は独立 (independent) という。
例えば、赤箱も青箱のオレンジ, リンゴの数がそれぞれ同じだったとき、
箱$B$が赤だろうと青だろうと果物が出る確率とは関係ない。これが独立。
$$
p(X, Y) = p(X)p(Y) = p(Y|X) p(X) \quad　(\mathrm{product \ rule}により)
$$
第2項と第3項を$p(X)$で割ると $p(Y) = p(Y|X)$ となり
$Y$の確率は条件$X$とは関係ない（独立）であることが数式としても導出できる

1.2.1 確率密度

これまで見てきた確率変数は離散値だった。これを連続値に拡張する。
$X=x$となるときの確率²を確率密度 (probability density) という。
(変数変換の話はよく分からない。とりあえずskipしても先の話の理解に困らないので飛ばす)
$x$が$(-\infty, z)$に存在する確率、言い換えると$x$が$z$以下に存在する確率 (を求める関数)を累積分布関数 (cumulative distribution function) という。
例：身長が170cm以下である確率

$$
P(z) = \int_{-\infty}^z p(x)dx
$$

1.2.2 期待値と分散

期待値を理解する簡単な例として歪なサイコロを考えよう。確率変数$X$は1~6をとる。関数$f$はサイコロの目と同じで $f(X=1) = 1, \cdots, f(X=6) = 6$となると定義する。確率分布は6の目は全く出ず、1~5の目が$p(1) = \cdots = p(5) = \frac{1}{5}$とすると、サイコロの目の平均値（期待値）は $1 \cdot \frac{1}{5} + \cdots + 5 \cdot \frac{1}{5} = 3$となる。
上の例のように、確率分布$p(x)$の下での関数$f(x)$の重み付き平均を期待値といい、
$ \mathbb{E}[f] $と書く。
- 離散値の場合： $$ \mathbb{E}[f] = \sum_x p(x) f(x) \tag{1.33} $$
- 連続値の場合： $$ \mathbb{E}[f] = \int p(x) f(x) dx \tag{1.34} $$
サイコロの例に戻る。十分な回数$N$回サイコロの目を観測すれば、
サイコロの目の平均値（期待値）はサイコロの目の総和を$N$で割った値で近似できる
ことが直観的に分かる。これをあらためて式で書くと
$$
\mathbb{E}[f] \simeq \frac{1}{N} \sum_{n=1}^N f(x_n) \tag{1.35}
$$
この近似は今後よく使う。

1.2.3 ベイズ確率

結論を先に言うと「ベイズ確率は人間の主観に基づく事前確率を確率論に使えること」がメリット
先のテキストの箱$B$と果物$F$の例でベイズの定理を眺めながら考えよう。今、愛媛県でこの箱と果物が目の前にあるとしよう $$ p(F | B) = \frac{p(B|F) p(F)} {p(B)} $$ ここで、推定したいのは箱の色$B$を見た後で果物$F$が何か？の確率$p(F|B)$であり、その確率の推定に箱の色を見る前の果物の確率$p(F)$（＝事前確率）が寄与している。この事前確率に人間の主観を入れて推定に使える。例えば、「愛媛県だし、たぶんリンゴよりみかんの確率の方が高そうだな」とか。
上の例は下手な例で分かりにくいが、事前確率に人間の主観を入れられると何が嬉しいのか？をの別例がテキストに記載されている。事前確率を使わないやり方（頻度主義という）で、コインが表になる確率の推定をするとしよう。3回コインを振って3回とも裏が出ると$p(表) = 0/3 = 0$ となり、このコインでは永遠に表がでないという推定になってしまう。
ベイズ確率では「コインだし、たぶん表の確率は0.5ぐらいでしょう」という事前確率をいれられる。これにより、3回中3回裏が出たとしても事前確率の影響で$p(表) = 0$とはならなくなる、これがメリット！
ただし、事前確率はあくまで人間の主観（や数学的に都合のいい）に基づいて設定されるので、頻度主義者 vs ベイズ主義者で対立があるらしい。この本はごりごりベイズ主義である

尤度 (likelihood)

下記私の説明より、kenmatsu4さんの説明がすごく分かりやすいです。
【統計学】尤度って何？をグラフィカルに説明してみる。

観測値があり、その観測値を生成した関数や確率分布を推定したいとき、尤度は「関数や確率分布の形を決めるパラメータ$\theta$をコレだと決めた（固定）したとき、本当に観測値がその関数/確率分布から生成される確率」を表している。
尤度が最大となるように関数/確率分布の形を決めるパラメータ$\theta$を推定する手法を最尤推定という。具体例は以下で。

最尤推定とMAP推定

最尤推定

曲線フィッティングに戻る。これは入力$x$に対する目的変数$t$を推定したいということだった。でも$t$には多少ノイズが入っているのでフィッティングした多項式曲線$y(x, w)$にぴったり一致した$t$となるわけではない。そこで、$x$に対応する$t$は$y(x, w)$に近い値で多少ばらつく。そこで、$t$が平均が$y(x, w)$、分散が$\beta^{-1}$なガウス分布に従うと考えよう。すると$t$は$x$とガウス分布の分散パラメータである$\beta^{-1}$と平均パラメータである$y(x, w)$を左右する$w$が与えられたときに確率的に決まる値と考えられるので、 $$ p( t | x, w, \beta ) = N( t | y(x, w), \beta^{-1} ) $$ と書ける。
平均$y(x, w)$、分散$\beta^{-1}$がある値だと決め打ちしたときに$t_1$から$t_N$までN個それぞれのデータが得られる確率の掛け算が尤度となり、尤度関数は
$$
p(t | x, w, \beta) = \prod^N_{n=1} N( t_n | y(x_n, w), \beta^{-1} )
$$
となる。この尤度が最大となるときのパラメータを推定値としましょう、というやり方が最尤推定。
実際に解いてみる。尤度が最大となるパラメータ$w$を求めることと対数尤度が最大となるパラメータを求めることは同値なので、数学的に便利な対数尤度で解こう。ガウス分布の定義である式(1.53)から

\begin{align}
\ln p(t | x, w, \beta) &= \sum^N_{n=1} \left[ \ln \frac{1}{ (2 \pi \beta^{-1} )^{1/2} }
\exp \left\{  - \frac{\beta}{2} (t_n - y)^2 \right\} \right] \\

&= \sum^N_{n=1} \left[ \ln \frac{1}{ (2 \pi \beta^{-1} )^{1/2} } \right] +
\sum^N_{n=1} \left[ \ln \exp \left\{  - \frac{\beta}{2} (t_n - y)^2 \right\} \right] \\

&= \sum^N_{n=1} \left[ \ln \frac{\beta^{1/2} }{ (2 \pi )^{1/2} } \right] +
\sum^N_{n=1} \left[ \left\{  - \frac{\beta}{2} (t_n - y)^2 \right\} \right] \\

&= - \frac{\beta}{2} \sum^N_{n=1} (y - t_n)^2 + \frac{N}{2} \ln \beta - \frac{N}{2} \ln ( 2 \pi )
\tag{1.62}

\end{align}

式(1.62)が最大となるパラメータ$w$を求めたい。$w$に関する項は第1項のみ、かつ負になっているので結局$\sum^N_{n=1} ( y(x_n, w) - t_n)^2$が最小になるような$w$が尤度を最大にすることになる。
- ノイズがガウス分布に従う前提での最尤推定による$w$の推定は、二乗和誤差の最小化と等価になった！

MAP推定

ベイズの定理を思い出そう。最尤推定は下式でいう尤度$p(D | w)$の最大化によりパラメータ$w$を求めるやり方だった。一方、MAP推定は尤度に事前確率$p(w)$をかけた事後確率$p(w | D)$を最大にするようなパラメータを求めようというやり方。ここで右辺の分母の$p(D)$はパラメータ$w$によらないので考慮しなくてよい！ $$ p(w | D) = \frac{p(D | w) p(w)} {p(D)} $$
天下りで、パラメータ$w$の事前確率は多次元ガウス分布に従うと仮定しよう。$w$は$w_0, \cdots, w_M$までのM+1次元であることに留意。 M+1次元の$w$はM+1次元のガウス分布に従う $$ p(w | \alpha) = N(w | \boldsymbol{0}, \alpha^{-1} \bf{I}) $$ これを多次元ガウス分布の定義式である式(1.52)に代入すると $$ p(w | \alpha) = \frac{1}{ (2 \pi)^{ \frac{M+1}{2}} } \cdot \frac{1}{| \alpha^{-1} \bf{I} |^{ \frac{1}{2} } } \cdot \exp \left\{ - \frac{1}{2} w^T (\alpha^{-1} \bf{I}) w \right\} \tag{1.65-A} $$ となり、式(1.65)を導出するには行列式の項の変形が必要になる。
行列式のイメージは、行列の張る空間の体積だと覚えよう。簡単のため、$ \alpha^{-1} \bf{I} $が3次元だとしよう。すると、
```
\begin{pmatrix}
\alpha^{-1} & 0           & 0 \\
0           & \alpha^{-1} & 0 \\
0           & 0           & \alpha^{-1}
\end{pmatrix}
```
と書ける。この行列の各列のベクトルが張る空間の体積を考える。すなわち、
- $\boldsymbol{u_1} = \{ \alpha^{-1}, 0, 0 \}^T$
- $\boldsymbol{u_2} = \{ 0, \alpha^{-1}, 0 \}^T$
- $\boldsymbol{u_3} = \{ 0, 0, \alpha^{-1} \}^T$

が張る空間の体積は$\alpha^{-3}$となる。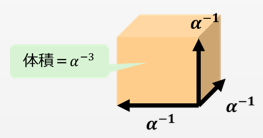
なので、この行列の行列式は$ | \alpha^{-1} \bf{I} | =\alpha^{-3}$。
- 同様にM+1次元の$ | \alpha^{-1} \bf{I} |$は$\alpha^{-(M+1)}$となる。これを(1.65-A)式に代入し、
式変形することで事前確率(1.65)式が導出できる。
$$
p(w | \alpha) = \left( \frac{\alpha}{2 \pi} \right) ^{(M+1)/2}
\exp \left\{ - \frac{\alpha}{2} w^T w \right\} \tag{1.65}
$$

後の計算のために事前確率の対数をとっておこう。

$$
\ln p(w | \alpha) = \frac{M+1}{2} \ln \left( \frac{\alpha}{2 \pi} \right)
- \frac{\alpha}{2} w^T w \tag{1.65-B}
$$

MAP推定では事後確率$p(w | D)$を最大とするパラメータを求めるが、最尤推定のときと同じように対数をとって対数事後確率を最大化するパラメータを求めよう。事後確率は尤度×事前確率に比例していたことを思い出すと対数事後確率は対数尤度＋対数事前確率で表せることが分かる。式(1.62)で導出した対数尤度と式(1.65-B)で導出した対数事前確率を足して、対数事後確率は

$$
- \frac{\beta}{2} \sum^N_{n=1} ( y(x_n, w) - t_n)^2 + \frac{N}{2} \ln \beta - \frac{N}{2} \ln ( 2 \pi )
+ \frac{M+1}{2} \ln \left( \frac{\alpha}{2 \pi} \right) - \frac{\alpha}{2} w^T w
$$

いま、パラメータ$w$に関して対数事後確率の最大化を行いたい。上式から$w$に関する項だけ抜き出すと

$$
- \frac{\beta}{2} \sum^N_{n=1} ( y(x_n, w) - t_n)^2 - \frac{\alpha}{2} w^T w
$$
となる。符号を反転させ、最大化問題を最小化問題に変形すると
$$
\frac{\beta}{2} \sum^N_{n=1} ( y(x_n, w) - t_n)^2 + \frac{\alpha}{2} w^T w \tag{1.67}
$$
となり、(1.4)式で導出した正則化つきの誤差関数が導出された！

演習問題

Exercise 1.5

式(1.38)を普通に展開すると

\begin{align}
var[f] &= \mathbb{E} \Bigr[ (f(x)^2 - 2f(x) \mathbb{E}[f(x)] + 
(\mathbb{E}[f(x)])^2 \Bigr] \\
       &= \mathbb{E} \Bigr[ (f(x)^2 \Bigr] 
-2 \mathbb{E} \Bigr[ f(x) \mathbb{E}[f(x)] \Bigr]
+ \mathbb{E} \Bigr[ (\mathbb{E}[f(x)])^2 \Bigr] \\
       &= \mathbb{E} \Bigr[ (f(x)^2 \Bigr] 
-2 \mathbb{E} \Bigr[ f(x) \mathbb{E}[f(x)] \Bigr]
+ \mathbb{E}[f(x)]^2 \tag{E1}
\end{align}

$\mathbb{E} \Bigr[ (\mathbb{E}[f(x)])^2 \Bigr]$は期待値の2乗の期待値を表すが、
期待値（サイコロでいう3.5）の2乗は固定値なので、固定値の期待値は固定値のまま。
なので$\mathbb{E} \Bigr[ (\mathbb{E}[f(x)])^2 \Bigr] = \mathbb{E}[f(x)]^2$と
書ける。

また、ここで$-2 \mathbb{E} \Bigr[ f(x) \mathbb{E}[f(x)] \Bigr]$に注目する。
$\mathbb{E}$の中の$\mathbb{E}[f(x)]$は定数（サイコロでいう3.5）なので$\mathbb{E}$の外に出せる。なので、

-2 \mathbb{E} \Bigr[ f(x) \mathbb{E}[f(x)] \Bigr]
= -2 \mathbb{E}[f(x)] \cdot \mathbb{E}[f(x)]
= -2 \mathbb{E}[f(x)]^2

これを式(E1)に代入すると式(1.39)が得られた。

世の中には3社しかなく、このどれか1つを必ず使っていると仮定 ↩
厳密にはこれは正しくなく、$x$が$(x, x+\delta x)$の微小な範囲に存在する確率、という方が正しい。$X=x$一点の確率が0でないと式(1.26)のように$(- \infty, \infty)$の範囲で積分すると非ゼロになってしまい、確率の定義を満たさなくなる。 ↩

PRML復活の呪文 part2 (1.2 - 1.2.3)