TL;DR
- 複数の「層」の重み$w$と非線形関数を使って入力$x$から所望の出力$y$を得ようとするモデルがニューラルネットワーク
- 重み$w$を推定するための準備として誤差関数を導出する
5 ニューラルネットワーク
線形回帰モデルや線形識別モデルでは、以下の式で表される固定された基底関数の線形和で表されるモデルを考えてきた。
$$
y(x, w) = \sum_{j=0}^{M-1} w_j \phi_j(x) = w^T \phi(x) \tag{3.3}
$$
このようなモデルは解析的には扱いやすいが、入力データの次元およびデータの数に応じて計算量が大きくなり実用に使うのが難しい面がある(次元の呪い)。
例えば、以下の3.1章で紹介した計画行列は、式(3.3)のモデルの重み$w$の最尤解を求める際に出てくるものだが、行列の行数(たて)はデータ数、列数(よこ)は入力データの次元で決まる。
よって、入力データの次元およびデータの数が大きくなると計算量が増えて辛くなることは想像にたやすい。
\begin{align}
\Phi =
\begin{pmatrix}
\phi_0(x_1) & \phi_1(x_1) & \cdots & \phi_{M-1} (x_1) \\\
\phi_0(x_2) & \phi_1(x_2) & \cdots & \phi_{M-1} (x_2) \\\
\vdots \\\
\phi_0(x_N) & \phi_1(x_N) & \cdots & \phi_{M-1} (x_N)
\end{pmatrix}
\tag{3.16}
\end{align}
5.1 フィードフォワードネットワーク関数
入力データ$x$が$D$次元である ($x_1, \cdots, x_D$) とし、これと重みの線形和で以下のように値$a_j^{(1)}$を求めよう。
$$
a_j^{(1)} = \sum_{i=1}^D w_{ji}^{(1)} x_i + w_{j0}^{(1)} \tag{5.2}
$$
ここで、$j$は$ j = 1, \cdots, M$であり、値$a$を何個作るかを示している。上付きの(1)はニューラルネットワークの何層目に属しているかを示すものであり、詳細はすぐ後で出てくる。$ w_{j0}^{(1)} $はバイアスであり、$ a_j^{(1)} $は活性 (activation) と呼ばれる。
...なんか小難しいが、(5.2)式の$a_j^{(1)}$を$y$と読み替えると3章や4章でやった以下の式と同じことを言っているだけである。
$$
y(x, w) = w_0 + w_1 x_1 + \cdots + w_{M-1} x_{M-1} = w_0 + \sum_{j=1}^{M-1} w_j x_j
$$
さて、式(5.2)で計算した活性$a_j^{(1)}$に対して微分可能な非線形活性化関数$h(\cdot)$を使い、$z_j$なる値を計算する。微分可能であることは、後に出てくるパラメータの推定に必要な特性である。
$$
z_j = h( a_j^{(1)} ) \tag{5.3}
$$
非線形関数には、シグモイド関数やtanh関数がよく用いられる(これらの関数は微分可能)。深層学習の領域では、ReLUと呼ばれる非線形関数がよく用いられる(もちろん、この関数も微分可能)。
さて、$z_j$が基底関数の出力($\phi(x)$)と思えば、$z_j$と(式(5.2)とは別の)重みの線形和で活性が計算できる。
$$
a_k^{(2)} = \sum_{j=1}^M w_{kj}^{(2)} z_j + w_{k0}^{(2)} \tag{5.4}
$$
ここで、$k$は$ k = 1, \cdots, K$であり、出力値の次元を示している。
...(5.4)式の$a_k$を$y$と読み替えるとやはり3章や4章でやった以下の式と同じことを言っているだけである。
$$
y(x, w) = w_0 + \sum_{j=1}^{M} w_j \phi_j(x)
$$
最後に、この$ a_k^{(2)} $に微分可能な非線形関数(活性化関数)を用いることで出力$y_k$を得る。
回帰問題では、活性化関数はふつう恒等写像であり、$y_k = a_k$である。
2クラス分類問題では、出力値が0~1の値をとってほしいので活性化関数によくシグモイド関数が用いられる。
$$
y_k = \sigma( a_k^{(2)} ) \tag{5.5}
$$
出力の活性化関数にシグモイド関数を用いた場合、式(5.2)~(5.5)をまとめると
$$
y_k(x, w) = \sigma \left(
\sum_{j=1}^M w_{kj}^{(2)} h
\left(
\sum_{i=0}^D w_{ji}^{(1)} x_i + w_{j0}^{(1)}
\right)
- w_{k0}^{(2)}
\right)
\tag{5.7}
$$
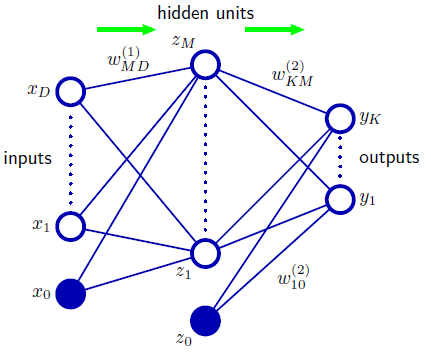
と書ける。これらの計算は下図のネットワークの形で表現できる。
- 左側の丸の列が入力層と呼ばれ、$x_1$から$x_D$までの丸は$D$次元入力データ$x$の値をそれぞれ表している($x_0$はバイアス)。入力層のそれぞれの丸は入力ユニットと呼ばれる。
- 真ん中の丸の列は隠れ層(中間層)と呼ばれ、隠れ層のそれぞれの丸は隠れユニットと呼ばれる。$z_M$に対応する隠れユニットにすべての入力ユニット$x_1, \cdots, x_D$から線が伸びている。
これは、$z_M$の値が$x_1, \cdots, x_D$の線形和で求まることを表している。つまり、
$ z_M = h ( \sum_{i=1}^D w_{ji}^{(1)} x_i + w_{j0}^{(1)} )$である。1本1本の線がある重み(1次元)を表している。 - バイアスに相当するユニット(上図では青塗りつぶし丸)は図上は省略されることが多い。
- 右側の丸の列は出力層と呼ばれ、$y_1$から$y_K$までの丸は$K$次元出力データ$y$の値をそれぞれ表している。出力層のそれぞれの丸は出力ユニットと呼ばれる。
- 式(5.7)は入力に相当する左側の入力層から出力に相当する右側の出力層まで情報が順伝播(じゅんでんぱ or じゅんでんぱん, forward propagation) していると解釈できる。後の節で出てくるが、学習の際は情報が右側から左側に逆伝播 (back propagation) する。
- 入力層、隠れ層、出力層の3層からなるネットワークなので、多くの文献では3層ネットワークと称される。しかし、テキストではネットワークの性質を決める重みが隠れ層と出力層の値のみに効いている(入力層は無関係)ことから2層ネットワークと呼ぶことを推奨している。本記事もこれに倣う。
上の例では隠れ層は1層のみだったが、2層以上に拡張することもできる。
上の例の2層ネットワークの場合は入力$x$から活性$a^{(1)}$を計算し、次に$a^{(1)}$から$a^{(2)}$および出力$y$を求めた。
この代わりに、$x$から$a^{(1)}$、$a^{(1)}$から$a^{(2)}$、$a^{(2)}$から$a^{(3)}$および出力$y$を求めるようにしてもよい。
深層学習では、何十層、何百層もの隠れ層からなるネットワークが使われている。
5.2 ネットワーク訓練
さて、ニューラルネットワークの重み$w$をどうやって学習するかを考える。
そこで誤差関数を定義し、誤差を最小にする$w$を求めるアプローチをとることとし、誤差関数の導出をする。
先に結論を言うと、誤差関数は導出するがニューラルネットワークの出力$y$は式(5.7)のような複雑な形で与えられるので、これまでの章でやったように誤差関数の$w$についての偏微分=0、の方程式を解くアプローチでは使えない。
具体的なアプローチは後の節で扱う。
回帰問題で目標変数が1次元の場合
1.1節「多項式曲線フィッティング」などでやったように二乗和誤差を最小にするアプローチをとろう。
すなわち、入力データの集合$ \{x_n\} (n=1, \cdots, N) $と対応する目標変数の集合$ \{t_n\} (n=1, \cdots, N) $が与えられたとき、誤差関数
$$
E(w) = \frac{1}{2} \sum_{n=1}^N || y(x_n, w) - t_n ||^2 \tag{5.11}
$$
を最小化することを考える。
後の解釈のために、ネットワーク出力$y$を確率的に解釈しよう。
目標変数$t$は$x$に依存する平均を持つガウス分布に従うとし、その平均はニューラルネットの出力で与えられる。すなわち、
$$
p(t | x, w) = N(t | y(x,w), \beta^{-1} ) \tag{5.12}
$$
とする。ここで、$ \beta $はガウスノイズの精度である。
$N$個の独立同分布に従う観測値$ X=\{ x_1, \cdots, x_N \}$とそれぞれに対応する目標値$ \mathbf{t} = \{ t_1, \cdots, t_N \} $からなるデータ集合が与えられたとき、尤度関数は:
\begin{align}
p( \mathbf{t} | X, w, \beta ) &= \prod_{n=1}^N p(t_n | x_n, w, \beta) \\
&= \prod_{n=1}^N \left( \frac{\beta}{2 \pi} \right)^{\frac{1}{2}} \exp
\left\{
- \frac{\beta}{2} (t_n - y(x_n, w) )^2
\right\}
\end{align}
である。尤度関数の負の対数を誤差関数とすると
$$
\frac{\beta}{2} \sum_{n=1}^N \{ y(x_n, w) - t_n \}^2 - \frac{N}{2} \ln \beta + \frac{N}{2} \ln (2 \pi ) \tag{5.13}
$$
が得られる。
※ニューラルネットの分野においては、重み$w$を求める問題を尤度最大化(最尤推定)と捉えず、誤差関数の最小化と考えることが多い。今回の例では尤度の最大化と誤差関数の最小化は符号が反転しているだけで本質的に全く同じ。
最尤推定のアプローチにより、$w, \beta$を推定することを考えよう。まずは$w$から。
式(5.13)から$w$に関する項を抜き出し、$\beta$を無視すると
$$
\frac{1}{2} \sum_{n=1}^N \{ y(x_n, w) - t_n \}^2 \tag{5.14}
$$
となり、二乗和誤差関数の最小化と等価であることが分かる。
これまでの章では、式(5.14)を$w$について偏微分=0、の方程式を解けば良かったが、ニューラルネットでは$ y(x_n, w) $が式(5.7)のようにややこしいのでこの方程式は解けない。
ひとまず、何らかの方法で推定解$ w_{ML} $が求まったとしよう。
次は$\beta$を求める。これは式(5.13)を$\beta$について偏微分=0、の方程式を解けば良い。
\begin{align}
(5.13) = & \frac{\beta}{2} \sum_{n=1}^N \{ y(x_n, w_{ML} ) - t_n \}^2 - \frac{N}{2} \ln \beta + \frac{N}{2} \ln (2 \pi ) \\
\betaについて偏微分=0の方程式は \\
& \frac{1}{2} \sum_{n=1}^N \{ y(x_n, w_{ML} ) - t_n \}^2 - \frac{N}{2} \cdot \frac{1}{\beta} = 0 \\
& \sum_{n=1}^N \{ y(x_n, w_{ML} ) - t_n \}^2 = N \cdot \frac{1}{\beta} \\
& \frac{1}{\beta} = \frac{1}{N} \sum_{n=1}^N \{ y(x_n, w_{ML} ) - t_n \}^2
\tag{5.15}
\end{align}
$ \beta $は$w_{ML}$が求まってからしか推定できないことに注意。
目標変数が多次元のとき(演習5.2)
多次元($K$次元)目標変数$ \mathbf{t} $の$i$次元め$ t_i $は出力の$i$次元め$ y_i $は相関関係があるが、出力の$j$次元め$ y_j (j \neq i) $には相関関係がないと仮定する。
また、ガウスノイズの精度がどの次元めでも共通であると仮定すると、ガウス分布の共分散行列は対角行列、かつ対角成分はすべて等しく$ \beta^{-1} $と書けるので目標変数の条件付き分布は:
$$
p(\mathbf{t} | x, w) = N(\mathbf{t} | y(x,w), \beta^{-1} I ) \tag{5.16}
$$
で与えられる。目標変数が1次元のときと同じ考えで尤度関数は
\begin{align}
p( T | X, w, \beta ) &= \prod_{n=1}^N p( \mathbf{t}_n | x_n, w, \beta) \\
&= \prod_{n=1}^N \frac{1}{ (2 \pi)^{K/2} } \frac{1}{ |\beta^{-1} I|^{1/2} } \exp
\left\{
- \frac{\beta}{2} (\mathbf{t}_n - y(x_n, w) )^T (\mathbf{t}_n - y(x_n, w) )
\right\} \\
&= \prod_{n=1}^N \left( \frac{ \beta }{ 2 \pi} \right)^{K/2} \exp
\left\{
- \frac{\beta}{2} (\mathbf{t}_n - y(x_n, w) )^T (\mathbf{t}_n - y(x_n, w) )
\right\}
\end{align}
ここで、$ T = \{ \mathbf{t_1}, \cdots, \mathbf{t_N} \}$である。負の対数(=誤差関数)をとると、
$$
\frac{\beta}{2} \sum_{n=1}^N (\mathbf{t} _ n - y(x_n, w) )^T (\mathbf{t}_n - y(x_n, w) )
- \frac{NK}{2} \ln \beta + \frac{NK}{2} \ln ( 2 \pi ) \tag{A}
$$
である。$w$を推定したいので、$w$に関する項を抜き出し$ \beta$は(定数とみなせるので)無視すると:
$$
\frac{1}{2} \sum_{n=1}^N (\mathbf{t} _ n - y(x_n, w) )^T (\mathbf{t}_n - y(x_n, w) )
$$
シグマの中身が内積、すなわち$ \sum_i ( t_i - y_i(x_n, w) )^2 $になっていることに注意すると、これは(5.11)式の二乗和誤差と同じ式になっていることが分かる。
また、$w$の最尤解$w_{ML}$が求まったとして、$\beta$を推定しよう、
式(A)を$\beta$について偏微分=0、の方程式を解く。
\begin{align}
\frac{1}{2} \sum_{n=1}^N (\mathbf{t} _ n - y(x_n, w_{ML}) )^T (\mathbf{t}_n - y(x_n, w_{ML}) )
- \frac{NK}{2} \cdot \frac{1}{\beta} = 0 \\
\sum_{n=1}^N || y(x_n, w_{ML} ) - \mathbf{t} _ n ||^2 = NK \cdot \frac{1}{\beta} \\
\frac{1}{\beta} = \frac{1}{NK} \sum_{n=1}^N || y(x_n, w_{ML} ) - \mathbf{t} _ n ||^2
\tag{5.17}
\end{align}
2クラス分類問題のとき
1次元の目標変数$t$が$ t=1 $のときにクラス$ C_1 $、$ t = 0$のときにクラス$ C_2 $を表すとする。
出力値が0~1の範囲になるように、出力ユニットの活性化関数をシグモイド関数とするネットワークを考える。
$$
y = \sigma(a) = \frac{1}{ 1 + \exp( -a )} \tag{5.19}
$$
$y$は条件付き確率$ p(C_1 | x)$と解釈でき、$ p(C_2 | x)$は$ 1 - y$で与えられる。
なので、入力が与えられたときの目標の条件付き分布$ p(t|x, w) $は下式のベルヌーイ分布となる。
$$
p(t | x, w) = y(x, w)^t \{ 1 - y(x, w) \}^{1-t} \tag{5.20}
$$
なお、式(5.19)での$y$を$y(x,w)$と書き直してある。
よって負の対数尤度で与えられる誤差関数は
$$
E(w) = - \sum_{n=1}^N \{ t_n \ln y(x_n, w) + (1 - t_n ) \ln (1 - y(x_n, w) ) \} \tag{5.21}
$$
となる。この式はクロスエントロピー誤差関数と呼ばれる。
分類問題では誤差関数を二乗和誤差とするより、クロスエントロピー誤差関数としたほうが訓練が早くなる、汎化性能1が高まるということが知られている。
多クラス分類問題のとき
クラス数が$K$、$K$次元の目標変数$\mathbf{t}$が1-of-K符号化法で表されているとしよう。
つまり、正解のクラスが$C_i$ならば$ t_i = 1, t_j = 0 (i \neq j) $である。
出力ユニットの活性化関数にソフトマックス関数を用いる。
$$
y_k(x, w) = \frac{ \exp( a_k(x,w) )}{ \sum_j \exp( a_j(x,w) )}
$$
$ a_k(x,w) $は式(5.4), (5.5)に相当する出力ユニットの活性化関数に入力する前の値である。また、$ y_k(x,w) $は$K$次元出力$y$の$k$次元めである。
このとき、$ y_k(x,w) $は$ p(t_k = 1 | x )$、つまり入力$x$がクラス$C_k$である確率と解釈できる。
このときの誤差関数は
$$
E(w) = - \sum_{n=1}^N \sum_{k=1}^K t_{nk} \ln y_k (x_n, w) \tag{5.24}
$$
と導出できる。この式も(他クラス)クロスエントロピー誤差関数と呼ばれる。
-
(訓練データ集合とは別の)未知のデータに対しても高い分類性能を持つこと。 ↩