はじめに
投稿遅れました🙇
こんにちは、元祖のヨッシーです。
今回は、通常のSegmentTreeを4分木にすると、実行速度が少し速くなったので記事を書いてみました。
セグメント木とは?
数列などの区間に対する操作(区間取得、一点変更)を高速にできるデータ構造
区間取得とは、例えば、数列のある区間の和、ある区間の最大値、最小値などを出すことができます
一点変更とは、数列上の一点の値を書き換える事ができます。
より詳細な仕様は
を見てください
しくみ
通常の2分セグメント木はこのような構造をしています(ここでは、区間和を持つセグメント木)
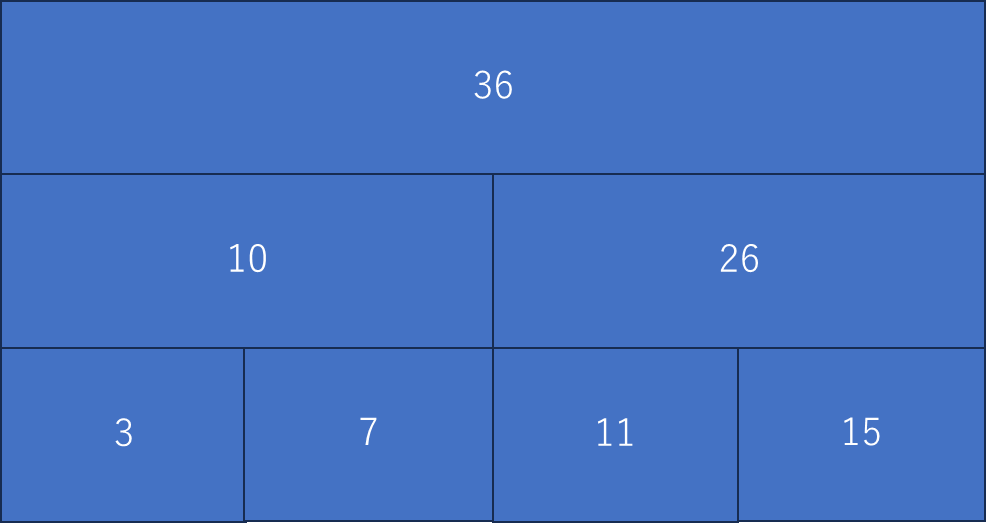
それぞれのノードが下の2つの区間の和を持っています
これを4つの区間を持つようにします
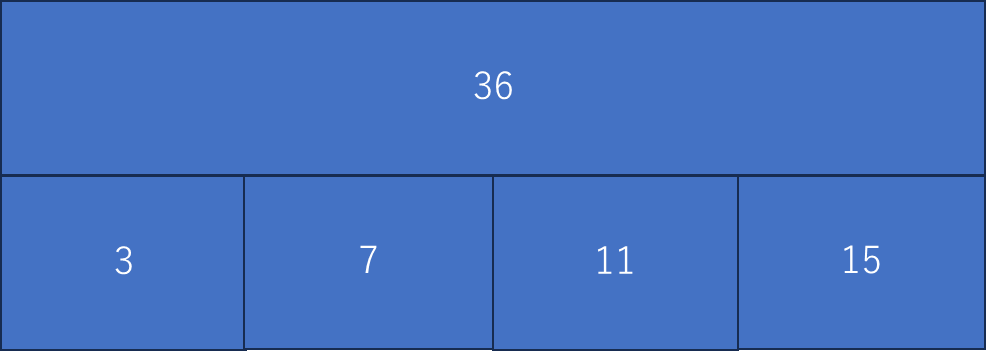
通常のセグメント木と4分セグメント木を比較します。
数列の長さを$N$とします
| 通常のセグメント木 | 4分セグメント木 | |
|---|---|---|
| 木の高さ | $log_2N+1$ | $log_4N+1$ |
| 全体のノード数 | $2N-1$ | $\frac{1}{3}(4 N - 1)$ |
| 1点変更の計算量 | $O(NlogN)$ | $O(NlogN)$ |
| 区間取得の計算量 | $O(NlogN)$ | $O(NlogN)$ |
操作の計算量はどちらも変わっていませんが、4分セグメント木は通常のセグメント木と比べてキャッシュ効率が良いらしいです。英語読める方はこちらもチェックしてみてください↓
実装
ac-libraryのセグメント木をベースに実装しました。
prodのところで、交換法則を要求しないように注意して実装しましょう。
実行結果
5回実行して平均のタイムを取りました。単位はミリ秒です。測定用のコードは後ろにあります。
環境
CPU:AMD Ryzen 7 5800H with Radeon Graphics
メモリ:16.0GB
Visual Studio 2022 C++
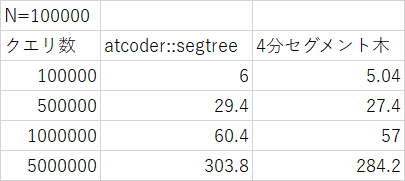
4分セグメント木が少し速いようです
オンラインジャッジ(参考)
AtCoder Library Practice Contest - J - Segment Tree
通常のセグメント木:58 ms https://atcoder.jp/contests/practice2/submissions/60878934
4分セグメント木:57 ms https://atcoder.jp/contests/practice2/submissions/60878927
AtCoder Library Practice Contest - B - Fenwick Tree
通常のセグメント木:167 ms https://atcoder.jp/contests/practice2/submissions/60879098
4分セグメント木:164 mshttps://atcoder.jp/contests/practice2/submissions/60879101
AtCoder Beginner Contest 185 - F - Range Xor Query
通常のセグメント木:106 ms https://atcoder.jp/contests/abc185/submissions/60879230
4分セグメント木:105 mshttps://atcoder.jp/contests/abc185/submissions/60879232
コード
#include<bits/stdc++.h>
#include<atcoder/all>
using namespace std;
inline unsigned int __builtin_clz(unsigned int x) { unsigned long r; _BitScanReverse(&r, x); return 31 - r; }
inline unsigned int __builtin_ctz(unsigned int n) { unsigned long r; _BitScanForward(&r, n); return r; }
template <class S, auto Op, auto E>
struct SegmentTree {
S op(S a, S b)const { return Op(a, b); }
S e() const { return E(); }
private:
int _n, size, log;
std::vector<S> d;
pair<int, int> ceil_pow2(int n) {
int x = 0; int t = 1;
while ((t) < (unsigned int)(n)) t *= 4, ++x;
return make_pair(x, t);
}
void update(int k) { d[k] = op(op(op(d[4 * k], d[4 * k + 1]), d[4 * k + 2]), d[4 * k + 3]); }
public:
SegmentTree() : SegmentTree(0) {}
explicit SegmentTree(int n) : SegmentTree(std::vector<S>(n, e())) {}
explicit SegmentTree(const std::vector<S>& v) : _n(int(v.size())) {
auto to = ceil_pow2(_n);
log = to.first, size = to.second;
d = std::vector<S>(2 * size, e());
for (int i = 0; i < _n; i++) d[size + i] = v[i];
for (int i = size / 2 - 1; i >= 1; i--) {
update(i);
}
}
void set(int p, const S& x) {
assert(0 <= p && p < _n);
p += size;
d[p] = x;
for (int i = 0; i < log; i++) {
update(p >>= 2);
}
}
S get(const int& p) const {
assert(0 <= p && p < _n);
return d[p + size];
}
S prod(int l, int r) const {
assert(0 <= l && l <= r && r <= _n);
S sml = e(), smr = e();
l += size;
r += size;
while (l < r) {
if ((l & 3) == 1) {
sml = op(sml, d[l++]);
if (l < r) {
sml = op(sml, d[l++]);
}
if (l < r) {
sml = op(sml, d[l++]);
}
}
else if ((l & 3) == 2) {
sml = op(sml, d[l++]);
if (l < r) {
sml = op(sml, d[l++]);
}
}
else if ((l & 3) == 3) {
sml = op(sml, d[l++]);
}
if (l < r) {
if ((r & 3) == 3) {
smr = op(d[--r], smr);
if (l < r) {
smr = op(d[--r], smr);
}
if (l < r) {
smr = op(d[--r], smr);
}
}
else if ((r & 3) == 2) {
smr = op(d[--r], smr);
if (l < r) {
smr = op(d[--r], smr);
}
}
else if ((r & 3) == 1) {
smr = op(d[--r], smr);
}
}
l >>= 2;
r >>= 2;
}
return op(sml, smr);
}
S all_prod() const { return d[1]; }
template <bool (*f)(S)> int max_right(int l) const {
return max_right(l, [](S x) { return f(x); });
}
template <class F> int max_right(int l, F f) const {
assert(0 <= l && l <= _n);
assert(f(e()));
if (l == _n) return _n;
l += size;
S sm = e();
do {
while ((l & 3) == 0) l >>= 2;
if (!f(op(sm, d[l]))) {
while (l < size) {
l = (4 * l);
while (f(op(sm, d[l])) && (l & 3) != 3) {
sm = op(sm, d[l]);
l++;
}
}
return l - size;
}
sm = op(sm, d[l]);
l++;
} while (((l & -l) != l) || (__builtin_ctz((unsigned)l) & 1));
return _n;
}
template <bool (*f)(S)> int min_left(int r) const {
return min_left(r, [](S x) { return f(x); });
}
template <class F> int min_left(int r, F f) const {
assert(0 <= r && r <= _n);
assert(f(e()));
if (r == 0) return 0;
r += size;
S sm = e();
do {
r--;
while (r > 1 && (r & 3)) r >>= 1;
if (!f(op(d[r], sm))) {
while (r < size) {
r = (4 * r + 3);
while (f(op(d[r], sm)) && (r & 3) != 0) {
sm = op(d[r], sm);
r--;
}
}
return r + 1 - size;
}
sm = op(d[r], sm);
} while ((r & -r) != r || (__builtin_ctz((unsigned)r) & 1));
return 0;
}
};
unsigned op(unsigned a, unsigned b) {
return max(a, b);
}
unsigned e() {
return 0;
}
int main() {
const int n = 1000000, q = 100000;
std::mt19937 engine(42);
vector<unsigned>v(n), querya(q), queryb(q), querytype(q);
for (int i = 0; i < n; ++i) {
v[i] = engine();
}
for (int i = 0; i < q; ++i) {
unsigned a = engine(), b = engine(), c = engine();
querytype[i] = c % 2;
if (querytype[i] == 0) {
querya[i] = a % n;
queryb[i] = b;
}
else {
querya[i] = min(a % n, b % n);
queryb[i] = max(a % n, b % n) + 1;
}
}
SegmentTree<unsigned, op, e>seg(v);
//もしくは、atcoder::segtree<unsigned, op, e>seg(v);
unsigned num = 0;
std::chrono::system_clock::time_point start, end;
start = std::chrono::system_clock::now();
for (int i = 0; i < q; ++i) {
if (querytype[i] == 0) {
seg.set(querya[i], queryb[i]);
}
else {
num ^= seg.prod(querya[i], queryb[i]);
}
}
end = std::chrono::system_clock::now();
cout << num << endl;
cout << std::chrono::duration_cast<std::chrono::milliseconds>(end - start).count() << " ms" << endl;
}
まとめ
読んでいただきありがとうございました。
いかがでしたか?
4分セグメント木の方が速くてよかった...
Xもやってるので良かったらフォローしてください
https://x.com/yosshi9990
明日は、 @UHAsikakutou さんの、「そのWebサイト、外からキレイに見える?【metaタグ・OGP・Twitterカード】」です。
おまけ
要素数NのD分セグメント木(N,Dは自然数,D>=2)の全体のノード数は、${\sum_{k=0}^{\log_D(n)} \frac{N}{D^k}}$である、簡単な形に直せ
ただし、$\log_D(n)$は自然数と仮定して良い
高校数学(数学II)の知識で解けます。
これを簡単な形に直せるのが一番おもしろかった(小並感)