Python & OpenCVで画像処理 [ Tone Curve編 ]

#はじめに
この記事は, Tone Curveによる画像処理の紹介がメインです.
教科書にTone Curveは載っているけど, コードは載っていない...
どんなコードで実現できるのか気になった人向けになるかもしれません.

Tone Curveを知らない方で, この記事を読んでくださる方は
簡単に<この記事>の「導入」で知ってくださると, よいかと思います.

• トーンカーブ
• 出力画像(カラー, グレイスケール)
• 変換関数

の順に紹介します.

#動作環境

端末：Windows 10
コンソール：cmd(コマンドプロンプト)
python：3.6.8
仮想環境：venv

#目次

• ネガ・ポジ反転
• 折れ線型トーンカーブ
  • 折れ線型トーンカーブ1
  • 折れ線型トーンカーブ2
• S字トーンカーブ
• ガンマ変換のトーンカーブ
• ソラリゼーション
• ポスタリゼーション
• 2値化

#紹介
入力画像は以下の2つになります.

カラー	グレイスケール
グレイスケール化に関してはOpenCVのcv2.cvtColor()を使いました.

カラー画像, グレイスケール画像がどのように変化するか
紹介していきます.

また, 関数からの返り値を cv2.imwrite() 関数などで読み込めば
保存できます.
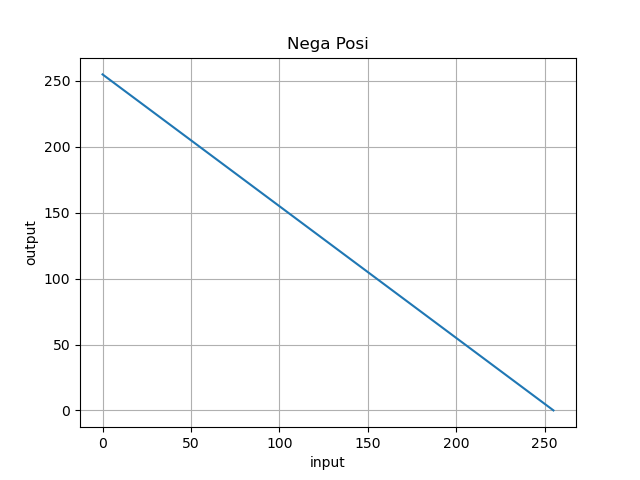
##▷ネガ・ポジ反転
画素値をその名の通り反転させます.
(※これより, 数式中の x は画素値です.)

f(x) = 255 - x

####トーンカーブ

####出力画像

• カラー

input	output

• グレイスケール

input	output

####関数

変換関数

def negaPosi(frame):
    return 255 - frame

##▷折れ線型トーンカーブ
以前紹介した記事と被ってしまいますが...
詳しく見たい方は, 記事を読んでくださるとありがたいです.

ここではn = 2についてのトーンカーブで出力します.
(※nは画素値を何倍するかの値です.)

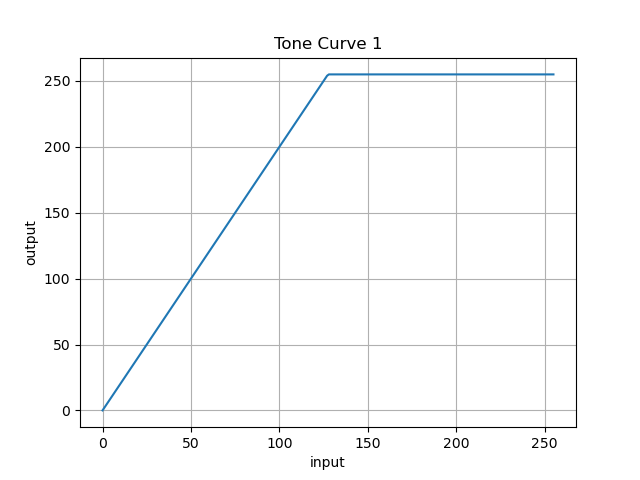
###◆折れ線型トーンカーブ1
画像のコントラストを上げる変換です.

f(x) = \begin{cases} 2 \cdot x & (x < 128) \\ 255 & (otherwise)
  \end{cases}

####トーンカーブ

####出力画像

• カラー

input	output

• グレイスケール

input	output

####関数

変換関数

def toneCurve1(frame, n = 1):
    look_up_table = np.zeros((256,1), dtype = 'uint8')
    for i in range(256):
        if i < 256 / n:
            look_up_table[i][0] = i * n
        else:
            look_up_table[i][0] = 255
    return cv2.LUT(frame, look_up_table)

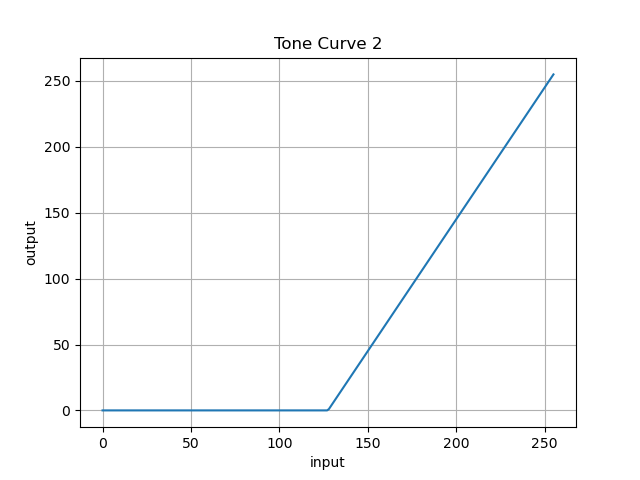
###◆折れ線型トーンカーブ2
上に対してこちらはコントラストを下げる変換です.

f(x) = \begin{cases} 0 & (x < 128) \\ 2 \cdot x - 255 & (otherwise)
  \end{cases}

####トーンカーブ

####出力画像

• カラー

input	output

• グレイスケール

input	output

####関数

変換関数

def toneCurve2(frame, n = 1):
    look_up_table = np.zeros((256,1), dtype = 'uint8')
    for i in range(256):
        if i < 256 - 256 / n :
            look_up_table[i][0] = 0
        else:
            look_up_table[i][0] = i * n - 255 * (n - 1)
    return cv2.LUT(frame, look_up_table)

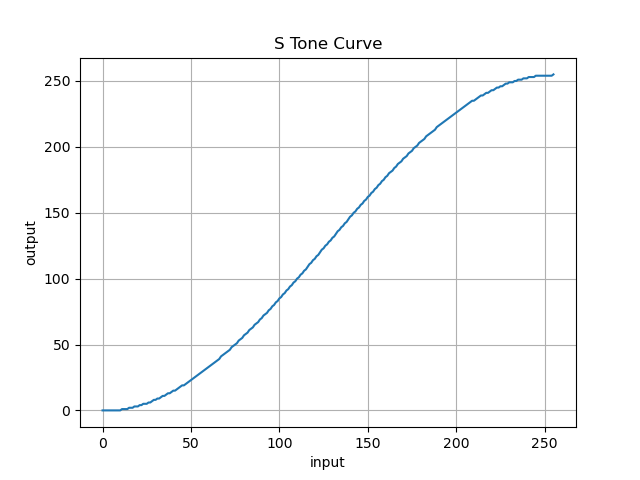
##▷S字トーンカーブ
今回のS Tone Curveは, 明るいところはより明るく
暗いところはより暗く強調する変換です.

f(x) = \frac {255}{2} \cdot \left\{\sin\left(\frac {x}{255} - \frac {1}{2}\right)\pi + 1\right\}

####トーンカーブ

####出力画像

• カラー

input	output

• グレイスケール

input	output
画像がどこかクリアになりました.
####関数

変換関数

def sToneCurve(frame):
    look_up_table = np.zeros((256,1), dtype = 'uint8')
    for i in range(256):
        look_up_table[i][0] = 255 * (np.sin(np.pi * (i/255 - 1/2)) + 1) / 2
    return cv2.LUT(frame, look_up_table)

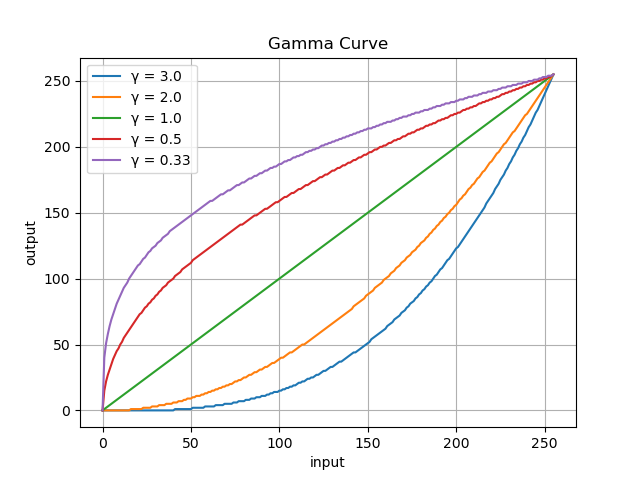
##▷ガンマ変換のトーンカーブ
先ほどの折れ線型トーンカーブでは
一定値(0, 255)に変換され, 濃淡情報が失われてしまった部分があるが
ガンマ変換では, その部分の濃淡情報も残しつつ変換を行えます.

f(x) = 255 \cdot \left(\frac {x}{255}\right)^\frac{1}{\gamma}

####トーンカーブ
いくつかの γ 値のパターンを示します.

####出力画像

• カラー

input	γ = 3	γ = 2
γ = 1	γ = 0.5	γ = 1 / 3

• グレイスケール

input	γ = 3	γ = 2
γ = 1	γ = 0.5	γ = 1 / 3
当たり前ですけど, γ = 1 とinputの画像は同じものになります.

####関数

変換関数

def gammaCurve(frame, gamma = 1):
    look_up_table = np.zeros((256,1), dtype = 'uint8')
    for i in range(256):
        look_up_table[i][0] = pow(i / 255, 1 / gamma) * 255
    return cv2.LUT(frame, look_up_table)

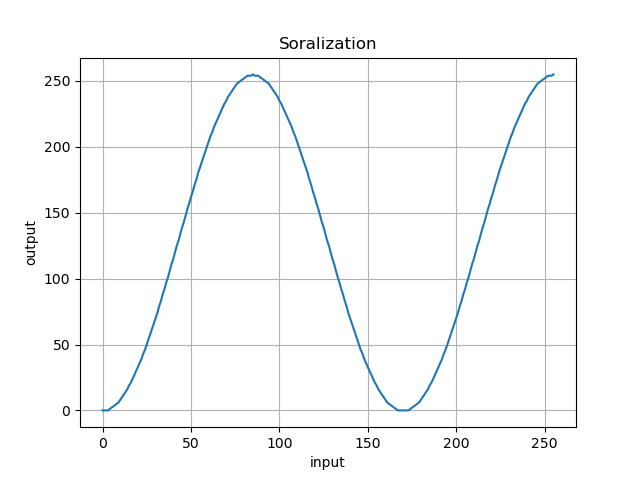
##▷ソラリゼーション
ネガとポジの画像が混ざり合ったような画像になります.

私のソラリゼーションで用いる変換数式は以下のようになります.

f(x) = \frac {255}{2} \cdot \sin\left\{3\pi\left(\frac {x}{255} - \frac {1}{2}\right)\right\}

####トーンカーブ

####出力画像

• カラー

input	output

• グレイスケール

input	output

####関数

変換関数

def soralization(frame):
    look_up_table = np.zeros((256,1), dtype = 'uint8')
    for i in range(256):
        look_up_table[i][0] = (np.sin(3 * np.pi * (i / 255 + 1 / 2 )) + 1) * 255 / 2
    return cv2.LUT(frame, look_up_table)

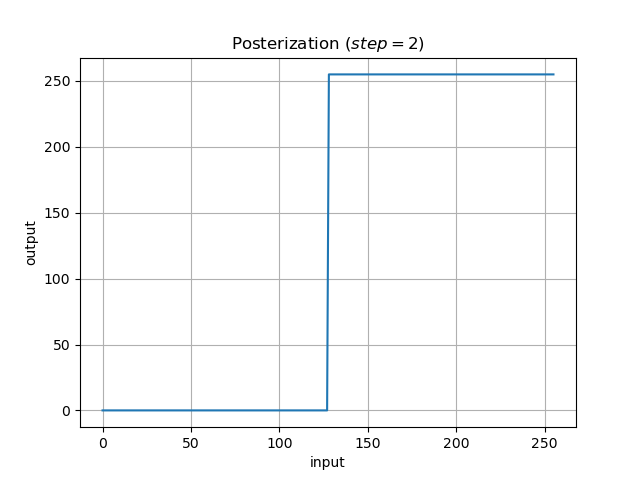
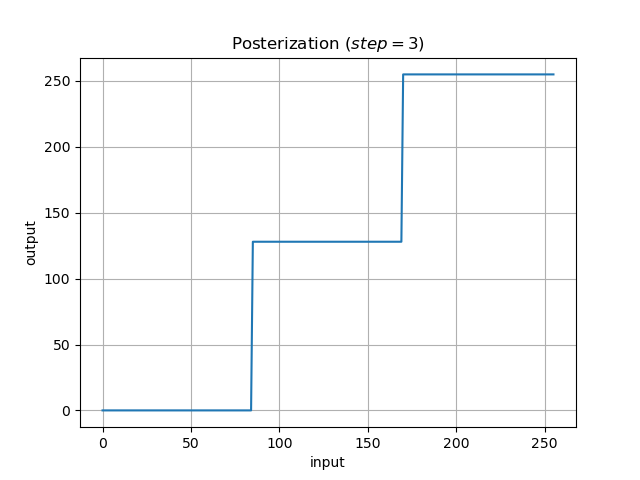
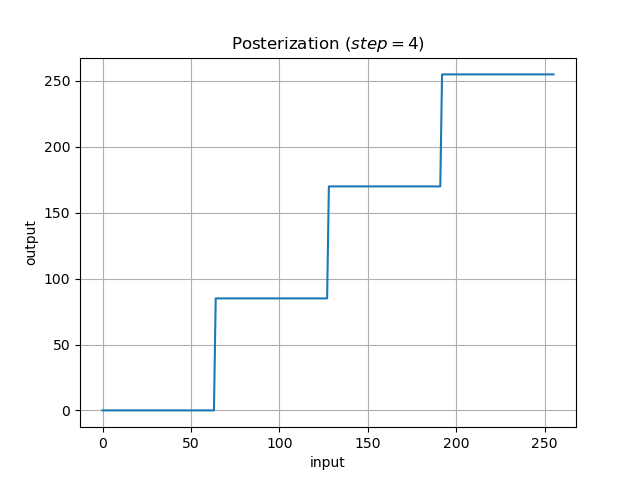
##▷ポスタリゼーション
画素値を段階的に一定値化します.
絵画のような画像になります.

出力としては, 画素値を2, 3, 4段階に分けたパターンを出力します.

####トーンカーブ
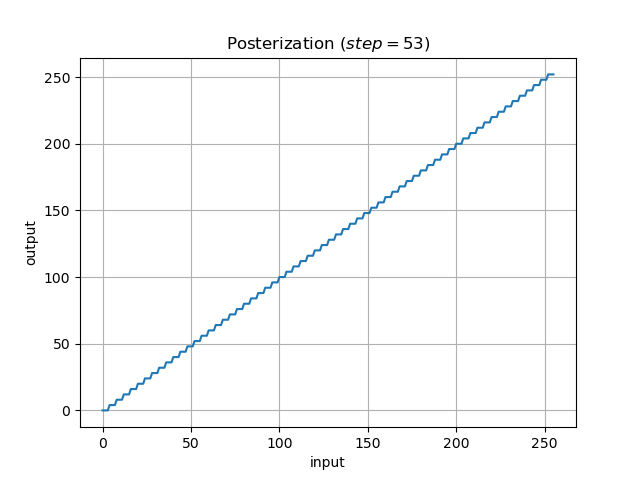
step = 53 はおまけです(余白的な問題で).

####出力画像

• カラー

input	step = 2
step = 3	step = 4

• グレイスケール

input	step = 2
step = 3	step = 4
ポストカードっぽくなりました.
####関数

変換関数

def posterization(frame, step = 4):
    if 1 < step and step <= 256:
        look_up_table = np.zeros((256, 1), dtype = 'uint8')
        split = int(256 / (step - 1))
        up = int(256 / step)
        for i in range(256):
            if np.trunc(i / up) * split >= 255:
                look_up_table[i][0] = 255
            else:
                look_up_table[i][0] = np.trunc(i / up) * split
        return cv2.LUT(frame, look_up_table)
    else:
        return frame

多分このコードが思いつくのに一番苦労したきがします...
もっといい方法がございましたら, ご教授ください.

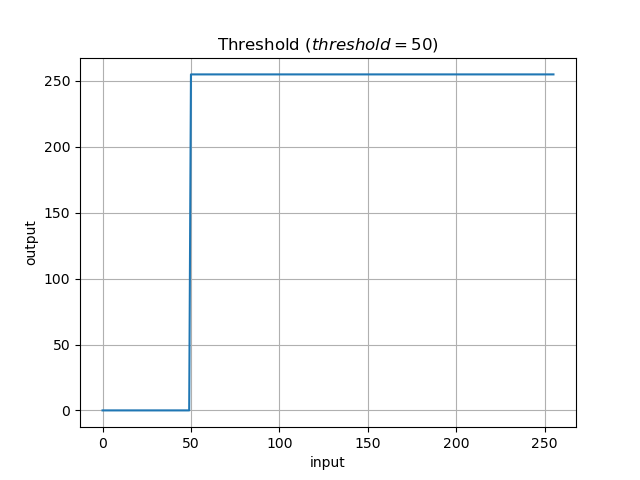
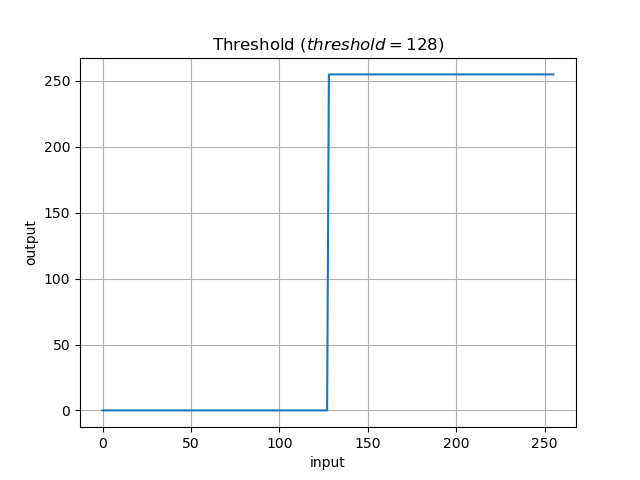
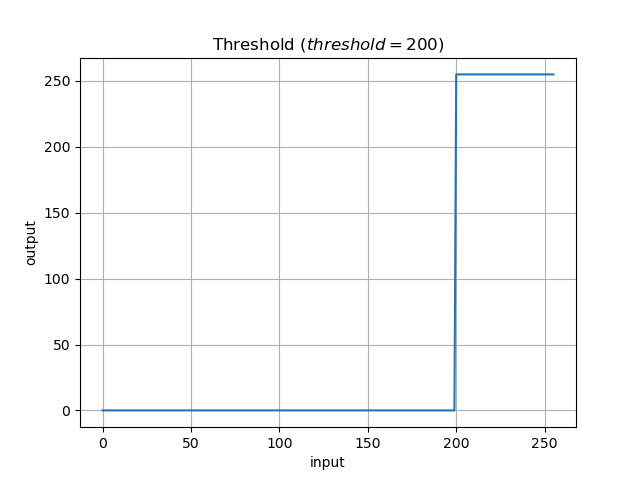
##▷2値化
閾値 n より
小さいときの値を0(最小値)
**大きいときの値を255(最大値)**にする変換です.

今回は使っていませんが, cv2ライブラリの中に二値化の関数があります.
cv2.adaptiveThreshold(), cv2.threshold() があります.

f(x) = \begin{cases}
       0 & (x < n) \\ 255 &(otherwise)
\end{cases}

####トーンカーブ
今回, 閾値 n = {50, 128, 200} の場合について出力します.

####出力画像

• カラー

| input |n = 50|
|:-:|:-:|:-:|:-:|
| | |
|n = 128| n = 200|
| | |

• グレイスケール

| input |n = 50|
|:-:|:-:|:-:|:-:|
| | |
|n = 128|n = 200|
| | |

####関数

変換関数

def threshold(frame, threshold_v = 50):
    frame[frame < threshold_v] = 0
    frame[frame >= threshold_v] = 255
    return frame

#メイン関数

ex.py

import cv2
import numpy as np

#関数群(省略)

def main():
    img_path = '.\\image\\castle.jpg' #任意に画像を指定
    img = cv2.imread(img_path)
    frame = grayScale(img)
    #関数を呼び出し, 実行してください.
    #例:
    # cv2.imwrite('tone_changed.jpg', negaPosi(img))

if __name__ == '__main__':
    main()

#おわりに
今回いくつかのトーンカーブによる諧調変換をつらつらと紹介しました.
次は, フィルタによる画像処理をやっていこうと思っています.

UIを追加して, 実用性を上げるでもよしですね.

それでは

#参考

• コンピュータ グラフィックス
• 画像取得元 (Pixabay)

#関連記事

• 画像処理のトーンカーブについての話しをしよう ~LUTはすごいぞ~