はじめに
ABテストを実施する上で、どちらの方が優れていたかを判断する基準として統計学的に判断する手法が一般的に使われています
利用するだけであればspreadsheetsやexcelなどでも関数が準備されているが名前を聞いたことがあるレベルだったので調べてみました。

今回t検定で何をやっているのか理解した範囲をアウトプットしてみたいと思います
T検定とは
t検定(ティーけんてい)とは、帰無仮説が正しいと仮定した場合に、統計量がt分布に従うことを利用する統計学的検定法の総称である。母集団が正規分布に従うと仮定するパラメトリック検定法であり、t分布が直接、もとの平均や標準偏差にはよらない(ただし自由度による)ことを利用している。2組の標本について平均に有意差があるかどうかの検定などに用いられる。
帰無仮説と対立仮説
| 用語 | 記号 | 説明 |
|---|---|---|
| 帰無仮説 | H0 | 群Aと群Bの母平均が同じであることを確認する 群Aの母平均 = 群Bの母平均 |
| 対立仮説 | H1 | 群Aと群Bの母平均が異なっていることを確認する 群Aの母平均 ≠ 群Bの母平均 |
| 有意水準 | p | 滅多に起きないだだろうと思える値を設定する 一般的には5%がよく利用される。 |
検定の流れとしてはこんな感じ
仮定: 帰無仮説 が正しい
群Aと群Bが同じ母平均
と仮定して今回取得されたデータの母平均の差が起きる確率を求める
今回取得されたデータの母平均の差が起きる確率が有意水準より低かった
↓
そんなレアなケースは起きないだろう
↓
仮定そのものが間違っているからだ!!
上のような流れで帰無仮説が間違っている → 対立仮説が正しいと主張をします。
母平均差の検定
2標本でt値を求める場合以下の式で導かれます。
t = \frac{(\bar{x_1} - \bar{x_2})}{\sigma \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}
\sigma^2 = \frac{(n_1-1)\sigma_1^2 +(n_2-1)\sigma_2^2}{n_1+n_2-2}
この時 tは自由度 n+m−2 の t分布に従う
記号をいきなり出してしまっているので整理したいと思います。
\begin{align}
\bar{x} &=標本平均 \\
\mu&= 母平均 \\
n &=それぞれの標本のサンプル数\\
\sigma &=プールした分散 \\
\sigma_1,\sigma_2 &=不偏分散 \\
\end{align}
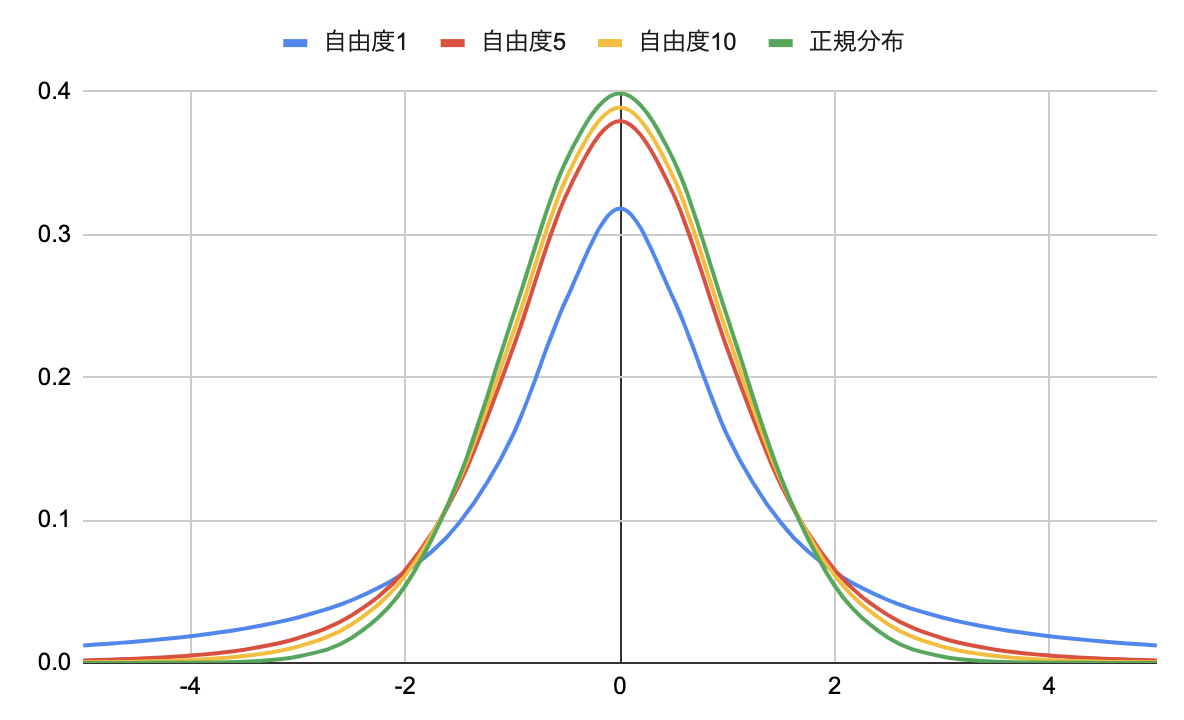
下に自由度1,5,10のt分布と正規分布のグラフをプロットしました。
サンプル数が大きければ大きいほど正規分布に近づくこととなります。
このグラフの面積が95%に入っているかどうかを見ていくわけです。
実際の数値を入れて計算
利用するデータは以下
あるクラスAとBの点数に有意差があるかどうかを確認したいとします。
有意差は5%とします。
| class A | classB |
|---|---|
| 95 | 99 |
| 100 | 74 |
| 87 | 89 |
| 94 | 95 |
| 61 | 93 |
| 98 | 92 |
帰無仮説、対立仮説を立てます。
- 帰無仮説
- クラスAとクラスBの学力は同じ - 対立仮設
- クラスAとクラスBのどちらかの学力が高い
次にclass Aの標本平均と不偏分散を求めてみる。
\begin{align}
\bar{x_1} &= \frac{\sum(x_i)}{n} \\
&= \frac{(95+100+87+94+61+98)}{6} \\
&= 89.16\\
\\
\sigma_1^2&= \frac{\sum(x_i - \bar{x})^2}{n-1} \\
&= \frac{(95-89.16)^2+(100-89.16)^2+(87-89.16)^2+(94-89.16)^2+(61-89.16)^2+(98-89.16)^2}{6-1} \\
&= 210.16 \\
\sigma_1 &=14.49
\end{align}
classBも同じように取得してみます。
| class A | classB | |
|---|---|---|
| 標本平均 | 89.16 | 90.33 |
| 不偏分散 | 14.49 | 8.66 |
次にプールされた分散σを計算します。
\begin{align}
\sigma^2&= \frac{(n_1-1)\sigma_1^2 +(n_2-1)\sigma_2^2}{n_1+n_2-2}\\
&=\frac{(6-1)14.49^2 + (6-1)8.66^2}{6+6-2}\\
&=142.61\\
\sigma&=11.94\\
\end{align}
最後にtを求めます。
\begin{align}
t &= \frac{(\bar{x_1} - \bar{x_2})}{\sigma \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \\
&= \frac{89.16-90.33}{11.94\sqrt{\frac{1}{6}+\frac{1}{6}}} \\
&= 0.16
\end{align}
ここで求めた0.16とT分布の表とを照らし合わせて有意差があるか確認します。
自由度10の両側0.05は2.228のため帰無仮説が採択された。
念のためスプレッドシートのT.TEST関数の結果と同じことを確認したとこと一致していることが確認できました。
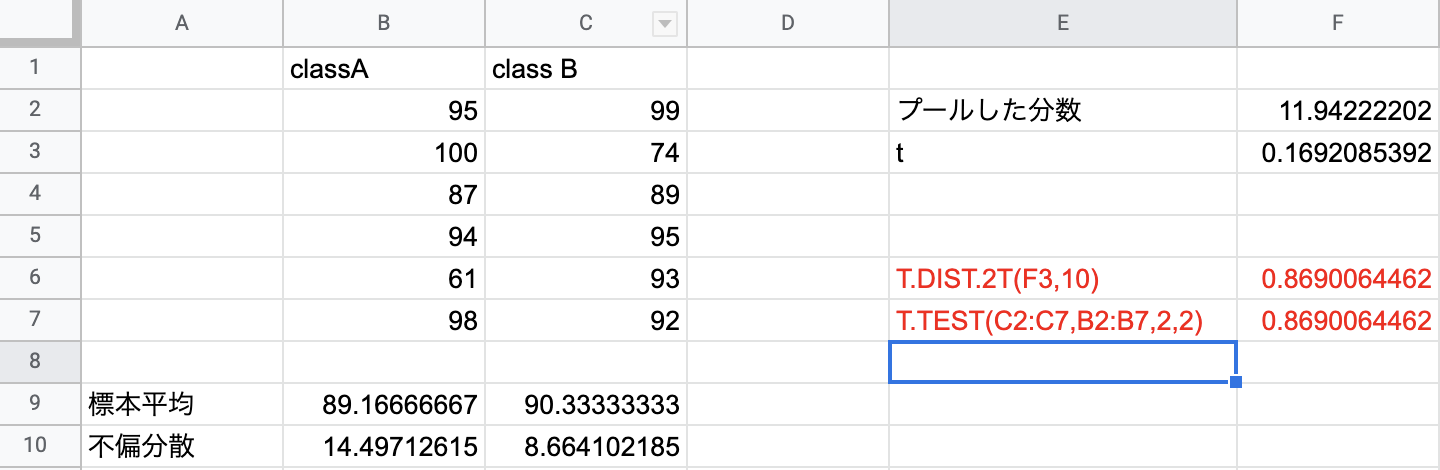
※ T.DIST , T.TEST はスプレッドシートに備わっている検定用の関数
終わりに
今回勉強したt検定の場合いくつかの条件を満たしていないと適応できません。
今後等分散ではない検定の方式としてウェルチの検定などもありますがまた別の際に読み進めてみようかと思います。
それではまた