仮想通貨取引所のPoloniexからAPI経由でデータ取得し、ディープラーニング（Chainer）で翌日の価格予測をしよう

はじめに

みなさま、こんにちは。
株式会社キカガク代表取締役の吉崎（Twitter: @yoshizaki_kkgk）です。

久々の休日にせっかくなら面白いことをしよう！と思いついたのが、今回の記事です。
ぜひ、読者の皆様にとって、データ解析のアプローチについて、理解の深まる記事となっておりましたら幸いです。

意外にも反響が！

前回、仮想通貨取引所のLiquiからデータをAPI経由で取得する初心者向けの記事を書きました。
前回の記事：仮想通貨取引所LiquiのAPIからPythonで情報を取得してみよう

今回この記事を書いた経緯

前回の記事に反響があったことももちろんですが、弊社で開催している「人工知能・機械学習 脱ブラックボックスセミナー」に参加されている受講生の方々から、この次のステップとして、「どのように勉強していけば良いですか？」といった質問を多くいただき、何か次のステップとして、渡してあげられるような技術記事を書きたいなと思っていました。

どのような技術記事を書けば、受講生の声にこたえてあげられるだろうと考え、下記を満たせる内容で何かないかと探していました。

• 本格的なデータが簡単に取得できる　→　仮想通貨
• 可視化したりデータの加工で楽しめる　→　時系列データ
• 最先端の手法の練習が出来る　→　ディープラーニング

そして、

うまくいけば、メリットがある

そういった経緯で、仮想通貨を題材に、最先端の時系列解析の手法まで紹介することに決めました。

今回のゴール

環境構築したり、データを取得しておしまいといった記事をよく見かけますが、私自身、最初から最後まで説明してある記事を読みたいなといつも思っているため、自分のためにも他の人のためにも面白いなと思える記事を今回も書いていきます。

• PythonでPoloniexのAPIを使うための環境構築しよう
• API経由でPoloniexのデータを取得しよう
• Pandasにデータを読み込み、移動平均を算出しよう
• Matplotlibでデータを可視化しよう
• 重回帰分析で翌日の価格を予測
• Chainerを使用して**RNN（LSTM）**で翌日の価格を予測

結論としては、ディープラーニングを使用した予測でもまだまだ改善の余地あり！といったところですが、まず試行錯誤の議論に入れるレベルまで本記事で書いていきます。
仮想通貨をはじめとした価格 / 需要予測は非常にニーズがあるのですが、まだまだ難しいといったことも体験していただければと思います。

また、こちらの手法を改良して、割と良い結果が得られたよ！という方は、私までご一報ください！
→ 吉崎（Twitter: @yoshizaki_kkgk）

#PythonでPoloniexのAPIを使うための環境構築
##Pythonの環境構築

まず、PCにPythonのインストールができていないよという方は、以下の記事の手順通りにインストールを行ってください。
弊社で主催しているセミナーで今まで数百人の方に行っていただきましたが、ほとんどエラーが出たことがない、設定の手順となっています。

Windows と Mac で設定手順が違うので気をつけてください。

・Windowsの方
【決定版】WindowsでPythonを使って『機械学習』を学ぶための環境構築

・Macの方
【決定版】MacでPythonを使って『機械学習』を学ぶための環境構築

Poloniexモジュールをインストール

Jupyter Notebookをまず開きましょう。

ターミナル（コマンドプロンプト / Windows Powershell）にて、以下のコマンドを実行すれば、ブラウザ経由で実行できる環境が立ち上がります。

jupyter notebook

実はJupyter Notebookでは、pipによるインストールができたりするので、いちいちターミナルを開かなくても良くて便利です。

Windowsの方はpipを使用し、Macの方はpip3を使用しましょう。
※ 私自身はMacで作業しているため、pip3を使用しております。

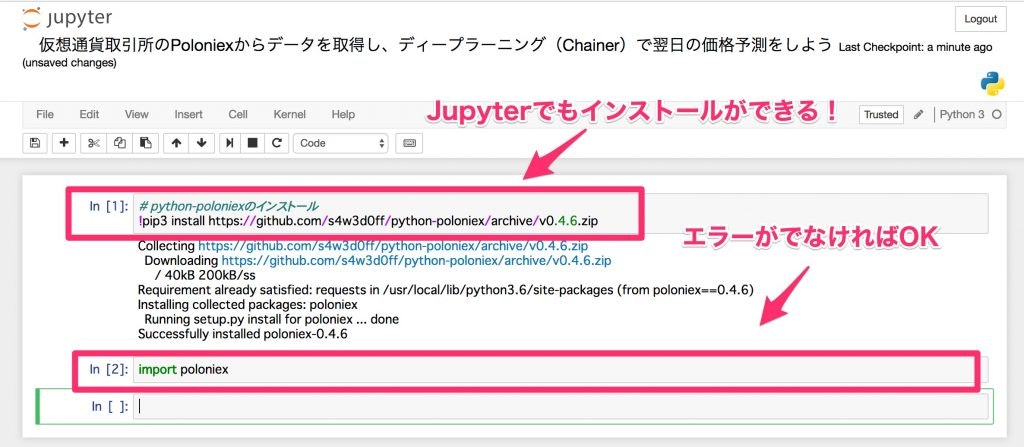
なお、Jupyter Notebook内でpipを使用する時は、一番最初に!を付ける必要があるので、お気をつけください。

# python-poloniexのインストール
!pip3 install https://github.com/s4w3d0ff/python-poloniex/archive/v0.4.6.zip

インストール後は、importを行い、正しくインストールされているか確認しましょう。

import poloniex

これでPoloniexからのデータをAPI経由で取得するための準備は完了です。

実は、PoloniexのAPIではURLを叩くことで、データを取得することが出来るのですが、それを更に使いやすくしたPython用のインターフェースが今回インストールしたpython-poloniexです。
こういった、機能としては同じですが、人間側にとって使いやすく（ラップ）したもののことを、ラッパー（wrapper）と呼び、プログラミングの業界ではよくこういったものも作られて公開されています。

API経由でPoloniexのデータを取得

データの取得

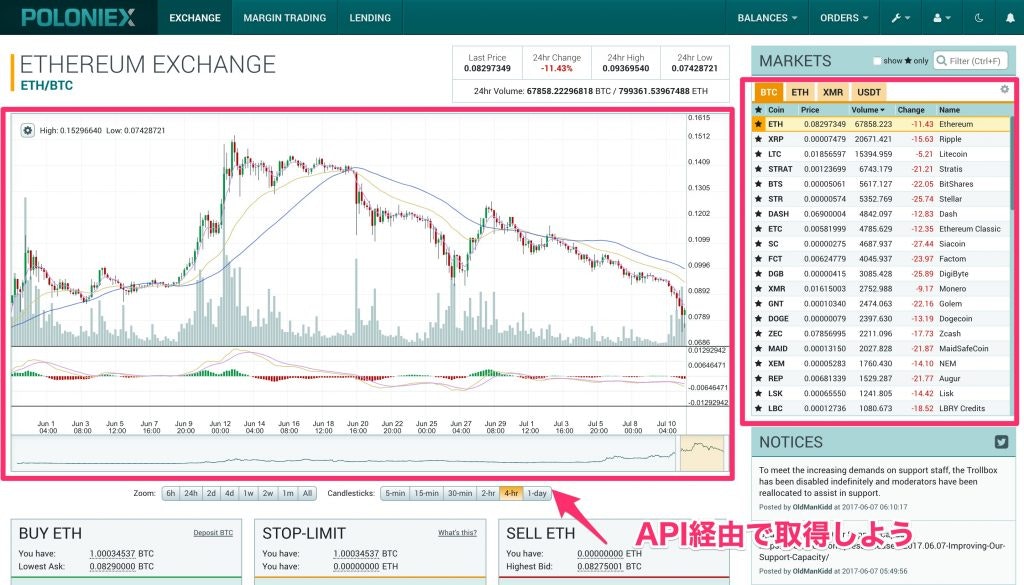
さて、これから本題であるPoloniexのデータ取得です。
Poloniexでは数年分のデータを一気に取得することができるため、自前で保存しておかなくても、過去のデータにアクセスすることができ、プロトタイプレベルの解析を行うには非常にありがたい環境です。

Poloniexラッパーのお陰で、以下のようにコマンド一行でデータを取得できます。
必要に応じて、サンプリング間隔や日数を調整しましょう。

import time

# poloniex APIの準備
polo = poloniex.Poloniex()

# 5分間隔（サンプリング間隔300秒）で100日分読み込む
chart_data = polo.returnChartData('BTC_ETH', period=300, start=time.time()-polo.DAY*100, end=time.time())

サンプリング間隔や日数（特にサンプリング間隔）に入れる値は、残念ながらGitHubに書かれているソースコードを読むしかありません。

Python-PoloniexのGithubページ

この中のソースコードをちゃんと読んでみると、以下のようなコメントが見つかります。

def returnChartData(self, currencyPair, period=False, start=False, end=False):
    """ Returns candlestick chart data. Parameters are "currencyPair",
    "period" (candlestick period in seconds; valid values are 300, 900,
    1800, 7200, 14400, and 86400), "start", and "end". "Start" and "end"
    are given in UNIX timestamp format and used to specify the date range
    for the data returned (default date range is start='1 day ago' to
    end='now') """

つまり、periodには 300(5分), 900(15分), 1800(１時間), 7200(4時間), 14400(８時間), 86400(12時間)が指定できます。
また、こちらのコメントにはありませんが、periodを１日間隔にしたい場合は、polo.DAYとすればOKです。

今回取得したデータを確認してみると、以下のような形式でデータが格納されていました。

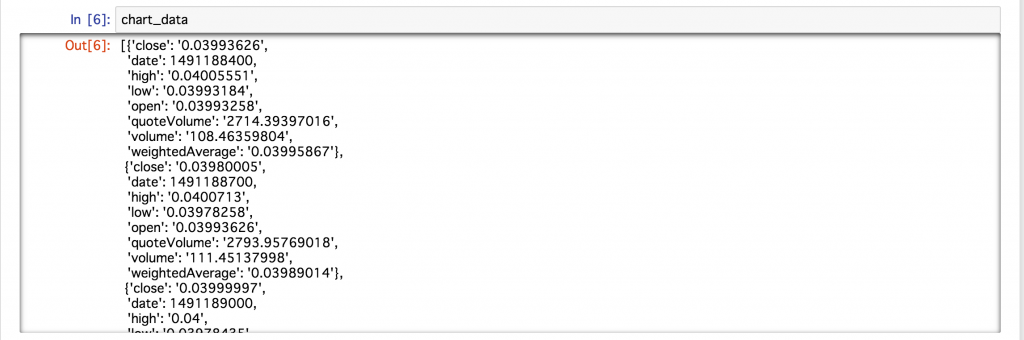
辞書型の中に上記のデータが各サンプリング時間ごとに格納されているようです。
このままでは、データとして扱いづらいので、データベース操作に便利なPandasを使って、効率良くデータの抽出を行っていきましょう。

Pandasにデータを読み込み、移動平均を算出しよう

Pandasにデータを読み込もう

Pythonでデータを操作する際は、間違いなくPandasが便利です（操作性＋参考記事の多さ）。
また、Jupyter Notebookを使用すると、テーブルの可視化も簡単かつ綺麗にできます。

Pandasへのデータの読み込みは簡単です。
特に、今回のように、各サンプリング時間ごとに、データのラベルと値が入っている場合は、PandasのDataFrameを使用するだけで読み込めます。

# pandasのインポート
import pandas as pd

# pandasにデータの取り込み
df = pd.DataFrame(chart_data)

もう既に、ご存知の方も多いと思いますが、

ModuleNotFoundError: No module named 'pandas'

のように、pandasっていうモジュールがないよというエラーが起きた場合は、

!pip3 install pandas  # !を付ければJupyter Notebook内でもインストールできる

のようにインストールすれば、すぐに使えるようになります（もしくはpip）。

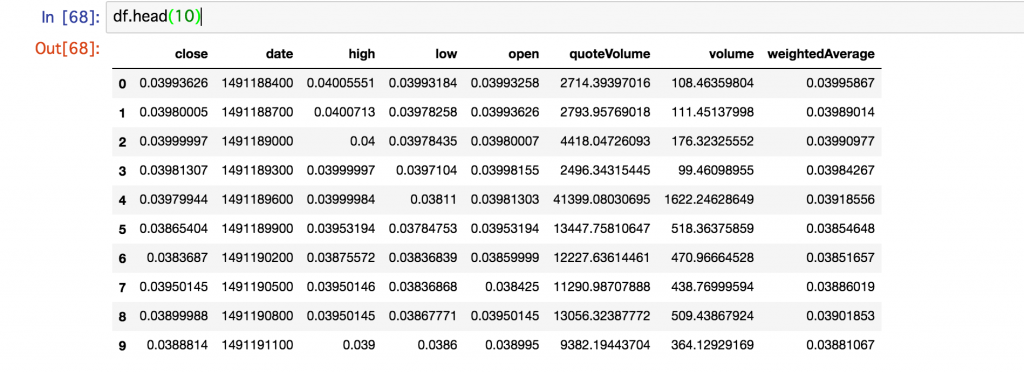
これで、最初の10行を表示してみましょう。

df.head(10)

エクセレント！

コマンドたった一発で簡単に読み込むことができ、非常に綺麗な形式でデータを確認できるため、データ解析の作業がはかどります！Pandasありがとう！

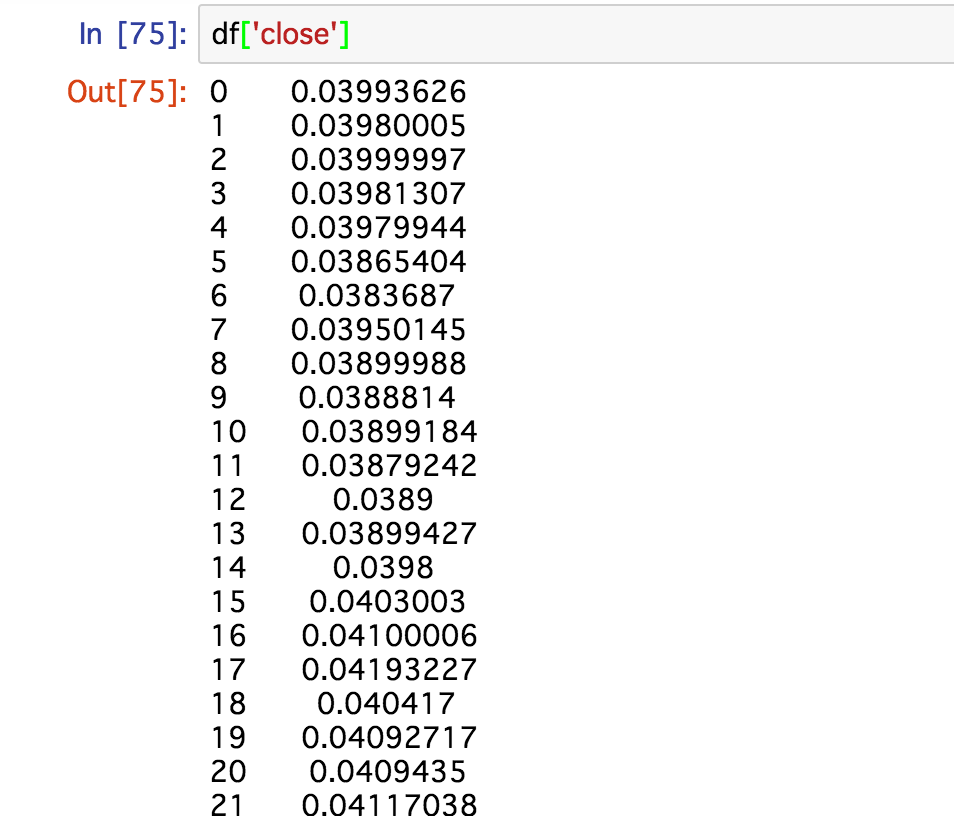
ちなみに、例えばcloseのカラムのみデータを抽出したい時は df['close']とカラムの名前をしてするだけで抽出できるため、非常に楽です。

移動平均を算出しよう

Pandasでは移動平均の計算も簡単に行うことができます。

今回は短期線として平均を算出する窓幅を１日、長期線として平均を算出する窓幅を５日としました。
移動平均を算出するためのソースコードは以下のとおりです。

# 短期線：窓幅1日（5分×12×24）
data_s = pd.rolling_mean(df['close'], 12 * 24) 

# 長期線：窓幅5日（5分×12×24×5）
data_l = pd.rolling_mean(df['close'], 12 * 24 * 5)

これで計算が完了です（簡単！）。
このぐらいであれば、窓幅を色々と変更してみて試せそうですね！

それでは、今回計算した移動平均も数値だけでは変化がわかりにくいため、プロットしてみましょう。

Matplotlibでデータを可視化しよう

まず使ってみよう

Matplotlibも言わずと知れたPythonの可視化ようのモジュール（ライブラリ）です。
百聞は一見にしかず！
さっそく、先ほどの移動平均も含め、プロットしてみましょう！

# matplotlibの読み込み（エラーが出た時はpip or pip3でインストール）
import matplotlib.pyplot as plt

# 一番簡単なプロット
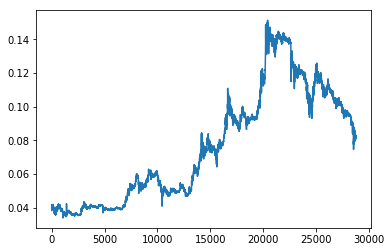
plt.plot(df['close'])
plt.show()

おっ！それらしい、時系列のグラフが表示されました。

Seabornでプロットを綺麗にしよう

Matplotlibでのプロットを更に綺麗にすることが出来る、MatplotlibのラッパーであるSeabornを使用していきます。
また、横幅も画面いっぱいに設定しておくと、見やすいため、こちらの設定も下記をコピペで少し変えておくと、解析が楽になりますよ。

# 描画を綺麗に表示する
from matplotlib.pylab import rcParams
import seaborn as sns
rcParams['figure.figsize'] = 15, 6

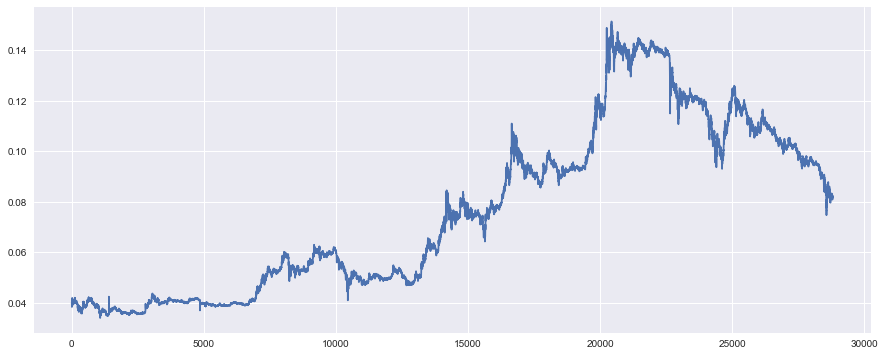
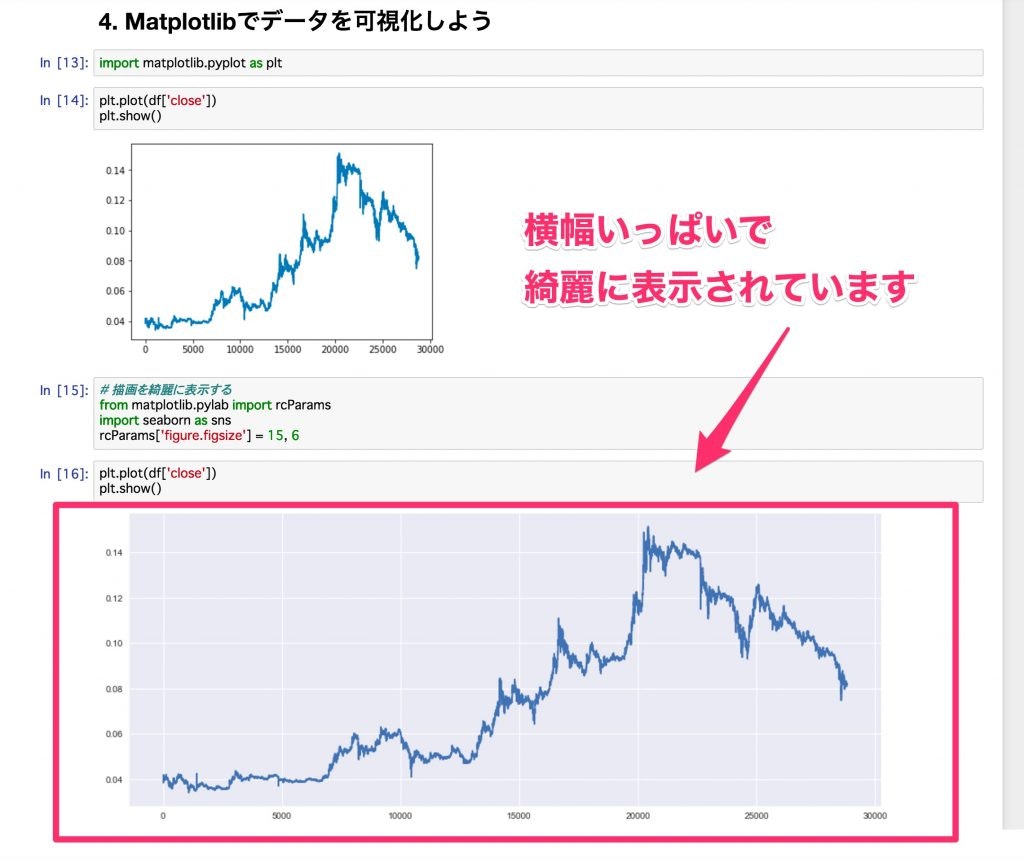
こちらで先ほどのデータをプロットしてみましょう。

横幅いっぱいで、グリッド線も入ったり、背景の色がついたりと、綺麗になったように感じます。
Jupyter Notebookでみると、このような感じで違いが一目瞭然です。

背景の色等はSeaborn側で変更することができるため、気になった方は下記の記事を参考にしてみてください。

参考：簡単に美しいグラフ描画ができるPythonライブラリSeaborn入門

プロットの色を変えてみよう

Matplotlibでは、色を替えることも非常に簡単です。
colorオプションに色の名前（例えばblueやred)でも良いですし、綺麗な色にこだわる人は16進数の #..... といった形式で指定すると良いと思います。

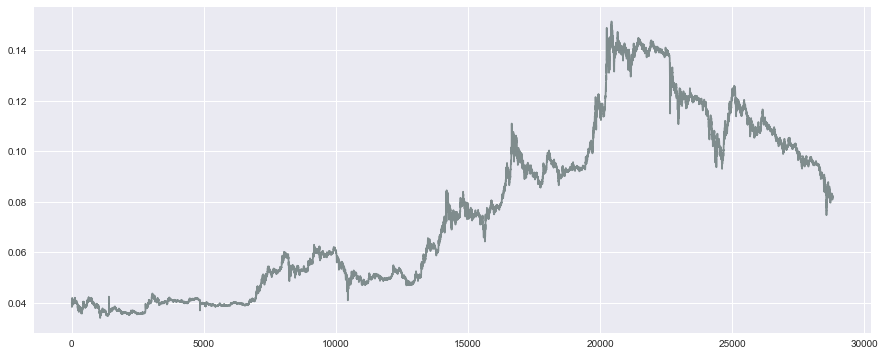
# プロットの色を指定しよう（color）
plt.plot(df['close'], color='#7f8c8d')
plt.show()

このように、色が変わりました。
今回の色は、こちらのFlat UI Colorsから選んできています。

参考：flat ui colors

短期線と長期線もプロットしよう

Matplotlibでは、複数の線をプロットすることも非常に簡単であり、表示したいものを宣言し、最後にplt.show()とすれば完了です。
それでは、先ほどPandas側で計算を行った短期線と長期線もあわせてプロットしてみましょう。

# 短期線と長期線もプロット
plt.plot(df['close'], color='#7f8c8d')
plt.plot(data_s, color='#f1c40f')  # 短期線
plt.plot(data_l, color='#2980b9')  # 長期線
plt.show()

良い感じにプロットできています！
これで数値だけでなく、どの程度の短期線と長期線の窓幅にすべきかといったことも、目視で判断できるようになりますね！

PandasとMatplotlibがあれば、数行でここまで解析ができてしまうなんて、本当にすごいですし、知らないと損ですね。

というわけで、ここまでがデータを取得して、簡単な集計、それから可視化を行いました。
ここからが、更に発展系の機械学習（人工知能の主要技術）を駆使したデータ解析手法をご紹介していきます。

このあたりは弊社のシステム自動化セミナーでさらに深く扱っていたりするので、興味のある方はぜひ！

重回帰分析で翌日の価格を予測

時系列データを扱う前提条件

それでは、機械学習技術による価格の予測が可能なものか気になる方が非常に多いと思いますので、実践形式で見ていきましょう。

**時系列データ（各時刻ごとに変動するデータ）**では、解析をする前提として、どのような特性を持っているかといった検定がたくさんあり、そもそもこの特性をクリアしていないとだめだよといった理論がたくさん議論されています。

もちろん、本来はちゃんと逐一確認していくべきだと思いますが、こういった細々とした性質を見ることが今回の本質ではなく、機械学習によって本当に価格の予測ができるのか！？といった結論をまず知りたいため、今回はこのデータの性質に関する議論は少し置いておきましょう。

こちらの性質について、深掘りしていきたい方は、以下の記事が色々な特性について詳しいためおすすめです。
参考：時系列データ分析の初心者に必ず知ってもらいたい重要ポイント ～ 回帰分析 ・相関関係 分析を行う前に必ずやるべきこと（データの形のチェックと変形）

直後の価格を予測しよう

それでは、まず機械学習では、入力変数Xと出力変数yの関係を紐付けていきます。
※ プログラム内では、出力変数の教師データはtとしており、出力変数の予測値をyとしています。

時系列データによる予測を行うとき、一番最初に現状のデータをどのような入力変数と出力変数に切り分けるかを考える必要があります。
今回は、予測したいもの（出力変数y）を５分後の価格として、その予測に用いる要因（入力変数X）を、直近30サンプル（5分×30個のデータ）としました。

このように切り分けるケースが多いですが、本当は単純な時系列のデータでなく、その差分をとったり、差分の対数をとったりすることが多いのですが、そのあたりの試行錯誤は次のステップとしておきましょう。

# 線形代数の演算でよく使うnumpyの読み込み
import numpy as np

# API経由では文字列（String型）として受け取るため、float型に変換しておく
# また、Chainerではfloat32を推奨しているため、こちらに合わせておく
data = df['close'].astype(np.float32)　

# データを入力変数xと出力変数tに切り分け
x, t = [], []
N = len(data)
M = 30 # 入力変数の数：直近30サンプルを使用
for n in range(M, N):
    # 入力変数と出力変数の切り分け
    _x = data[n-M: n] # 入力変数
    _t = data[n] # 出力変数
    # 計算用のリスト(x, t)に追加していく
    x.append(_x)
    t.append(_t)

また、後々の解析で使用する際に、サイズの確認など、numpyの形式でデータを格納しておくと、何かと便利なため、データを変換しておきます。

# numpyの形式に変換する（何かと便利なため）
x = np.array(x)
t = np.array(t).reshape(len(t), 1)  # reshapeは後々のChainerでエラーが出ない対策

訓練データ（train）と検証データ（test）に分ける

機械学習では、モデルを作って終わり！ではなく、作ったモデルでどの程度の精度が出ているかを確認（検証）するために、２つのデータに分割します。

• 訓練データ(train)：モデルを学習させる用のデータ
• 検証データ(test) ：答え合わせして精度を確認する用のデータ

※さらに発展形としては、ハイパーパラメータと呼ばれる手法内で手動で決定すべきパラメータを決定するためのデータに３分割するケースもあります。

まずは、この訓練データと検証データの２分割で、作ったモデルをしっかりと検証できるようになりましょう。
今回は、訓練データを全体の70%、検証データを全体の30%とします。

# 70%を訓練用、30%を検証用
N_train = int(N * 0.7)
x_train, x_test = x[:N_train], x[N_train:]
t_train, t_test = t[:N_train], t[N_train:]

Pythonのリストを切り分ける機能をうまく活用すれば、上記のように、簡単にデータセットを分割することができます。

重回帰分析のモデルを学習

Pythonでは機械学習のスタンダードとして、Scikit-learnがあります。
こちらでは、最先端にこだわらなければ、ほとんど全ての手法が実装されており、何より操作を行うインターフェースが非常に良いので、オススメです。

それでは、Scikit-learn（プログラム内ではsklearn）を使用したモデルの学習を実装していきましょう。

# scikit-learnのlinear_modelを読み込み
from sklearn import linear_model

# 重回帰分析モデルの宣言
reg = linear_model.LinearRegression()

# 訓練データを使ったモデルの学習
reg.fit(x_train, t_train)

はい。たったこれだけで完了です。
モデルを宣言して、訓練データをモデルに渡してfitすればOKです。
拍子抜けするぐらい簡単ですが、このシンプルなコードは人間側の間違いも少なくしてくれるため、非常にありがたいです。

データ解析でうまくいかない際に、データが悪いのか、プログラムが悪いのかがわかなくなることが多く、こういったライブラリを使用することで、自分の責任（プログラムのミス）を減らすことができるため、要因分析をスムーズに進めることができます。

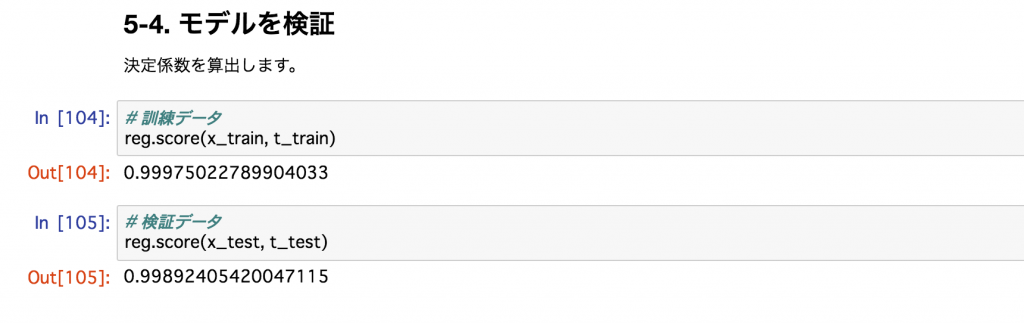
モデルを検証

先ほどの検証データを使用して、精度の検証を行いましょう。
精度の指標としては、決定係数と呼ばれる0〜1の間で計算される（厳密にはマイナスも取る）指標を用います。
ざっくりと、1であれば最高、0であれば論外といったところです（表現が極端すぎますが）。

また、検証する際には、検証データだけでなく、訓練データに対しても決定係数の値を見てあげましょう。
理想的には、この２つの値が同程度かつ、精度が高ければ、良いモデルといえます。

決定係数の計算にはscoreを使えばOKです。

# 訓練データ
reg.score(x_train, t_train)

# 訓練データ
reg.score(x_train, t_train)

上記のように、１に非常に近い値が出ており、以下のようなストーリー展開を想像します。

Welcome to お金持ち

「おっ！これはめちゃくちゃ良い精度で予測できているんじゃないか！明日から大金持ちかもしれない。」
「投資で儲かるから節税対策を考えなきゃ。」
「不動産はまずこのあたりのマンションから始めよう。よし、億ションを買おう。」

結果を可視化

それでは、決定係数が非常に良い値となっていた期待を胸に、実測値と予測値をプロットしてみましょう。

まずは、訓練データに対して、実測値（青色）と予測値（オレンジ）のプロット

# 訓練データ
plt.plot(t_train, color='#2980b9')  # 実測値は青色
plt.plot(reg.predict(x_train), color='#f39c12')  # 予測値はオレンジ
plt.show()

２つのデータが非常によく重なり合っており、ほとんど一致していることがわかります（期待値更に増）。
ただ、これは訓練に使用したデータのため、うまくいっていて当然。
本題は検証データに対する結果です。

それでは、検証データに対して、実測値（青色）と予測値（オレンジ）のプロット

# 検証データ
plt.plot(t_test, color='#2980b9')  # 実測値は青色
plt.plot(reg.predict(x_test), color='#f39c12')  # 予測値はオレンジ
plt.show()

おぉ！ばっちりこちらも重なっています！
素晴らしい！素晴らしすぎる！
これで大金持ちが確定したかもしれません。

みなさま、それでは次回はドバイで会いましょう。

早すぎた大金持ちからの転落

実は、これすごくうまくいっているように見えるのですが、本当は全然うまくいっていません。
残念ながら、ドバイはもう少し先になりそうです。
あぁ、億ション、、、笑

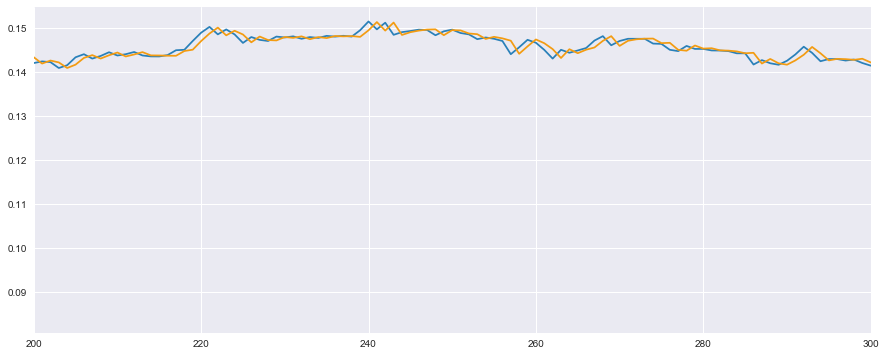
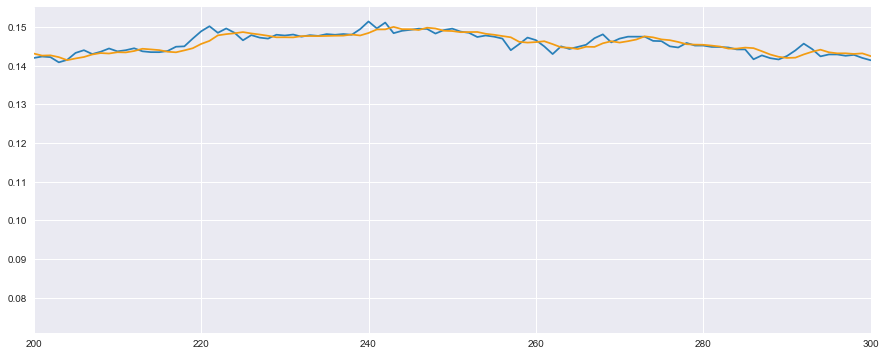
どういうことかと説明するため、全体ではなく、検証データの一部分を見てみましょう。
一部分を抜き出す時はplt.xlim()で範囲を指定してあげればOKです。

# 検証用の一部を見てみる
plt.plot(t_test, color='#2980b9')  # 実測値は青色
plt.plot(reg.predict(x_test), color='#f39c12')  # 予測値はオレンジ
plt.xlim(200, 300)  # 特徴がわかりやすい一部
plt.show()

実は一見うまく予測できているように見えるのですが、実測値（青色）に対して、予測値（オレンジ）が単純に１サンプル分だけずれているだけなのが見ていただいておわかりかと思います。

要するに、機械学習で学習させてなんかもっともらしい値が予測により出ていたかと思いきや、１サンプル前の値を予測値として出力していただけで、全然頭を使った方法ではなかったわけなんです。
５分前の値を予測値とすれば、たしかにもっともらしいような値が出てきて、決定係数は高く算出されるわけなんですね。

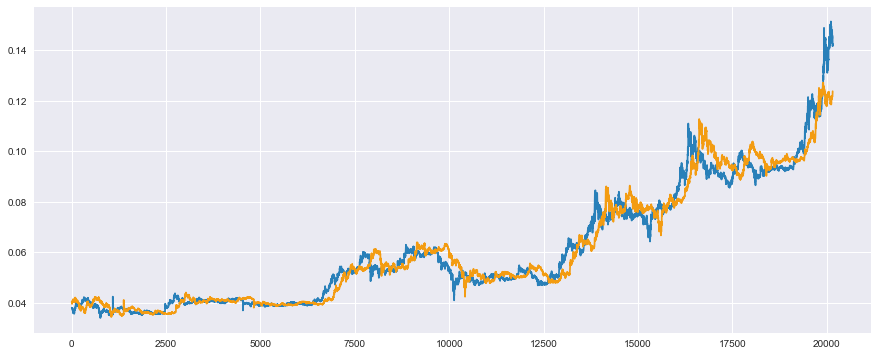
これを５分後の予測ではなく、１日後の予測に変えてみた場合はこのような結果が得られました。
※ このプログラムはみなさん、挑戦してみてくださいね。

これは訓練データに対する予測なのですが、非常に顕著に、予測値がデータを１日分（5分で1サンプル×12×24=288サンプル）ずらしただけといった結果が得られています。

これが需要予測はデータ解析によって実現することが非常に難しいと言われる理由だったりします。

なぜこうなるの？

多くの機械学習の手法では、誤差が全体を通して小さくなるようにモデル内のパラメータと呼ばれる値を調整して、うまくフィッティングできるようになります。
そして、今回のような時系列データでは、ランダムウォークと呼ばれる現象が起きており、これがパラメータ調整の難易度を上げています。

どういうことかというと、前サンプルに対して、その次のサンプルで値段が上がるか下がるかが確率でいうと５：５なのです。
５：５ということは平均（期待値）で考えると、次の価格は上がりも下がりもしないと考えるのが優等生的な機械学習の答えであったりします。
その結果、前日の値をそのまま翌日の値に反映することがベストだという理屈なのです。

これを機械学習ではデータから純粋にこの理屈を導き、予測値に反映しているわけです。

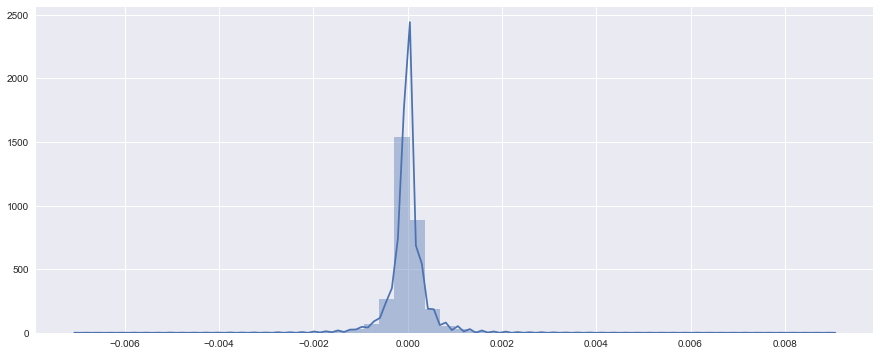
試しに、前日との価格の差分を見てみると、以下のようなヒストグラムになりました。

# 前サンプルとの差分を取る
t_diff = t[:-1] - t[1:]

# searbornのdistplotが便利
sns.distplot(t_diff)
plt.show()

ちょっとビン(bin)の幅が広いので、もう少し細かくして見てみます。
あと、プロットされている線（カーネル密度比推定の結果）は必要ないので、消しておきましょう。

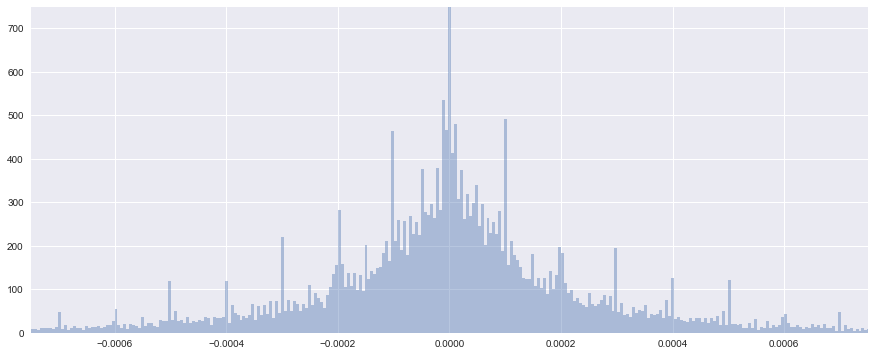
# binの数を増やし、kde(ガウシアンカーネル密度比推定)のプロットをオフ
sns.distplot(t_diff, bins=3000, kde=False)
plt.xlim(-0.00075, 0.00075)
plt.ylim(0, 750)
plt.show()

0よりも右半分が前日よりも価格が上昇した回数、0よりも左半分が前日よりも価格が下落した回数です。
見て分かる通り、ほぼ０を中心に左右対称に分布していることがわかります。
したがって、上がるか下がるかが５：５のランダムウォークになっているわけです。
補足：ランダムウォーク性の判定には目視ではなく、色々な統計的検定手法があるので、気になる方は調べてみてください。

どうすれば良いの？

重回帰分析をはじめとした機械学習の手法では、そもそも、データは各時刻毎に独立して真の分布から生成されると仮定しています。
つまり、前時刻のデータが次の時刻のデータに影響を与えない（真の分布からランダムに生成されるはず）ということを前提としています。

例えば、家賃を推定する問題の時に、１サンプル目にAさんのお家の条件（駅からの距離、部屋の広さ）が入っており、２サンプル目にBさんのお家の条件が入っていますが、特にAさんのお家がBさんのお家と関係性を持っているわけではない（独立に生成されている）ということです。

そのため、前時刻のデータが思いっきり影響を与える時系列解析の場合は、そもそも前提が異なっているため、当然うまくいくはずがないんですね。

この性質をモデル化したいと考えられたのが、隠れマルコフモデルです。
詳しい説明は下記の記事が素晴らしくわかりやすく解説してくれているので省略するとして、要するに、前のデータが次のデータに影響をあたえる場合でも予測できるような仕組みを作ったのです。

参考：時系列データ：隠れマルコフモデルの基礎と、リカレントネットの台等

そして、それが近年ブームになっているディープラーニングでも実装されており、Recurrent Neural Network、俗にいうRNNです。

というわけで、本記事の最後にこのRNNを使用したモデル化をご紹介して締めとします。

Chainerを使用してRNN（LSTM）で翌日の価格を予測

Chainerとは？

Chainerは日本の企業であるPreferred Networks社が開発をすすめるディープラーニング（ニューラルネットワーク）に特化したPythonで使用できるフレームワークです。
他にも、Googleが提供するTensorFlowやそのラッパーのKerasもあり、個人的には日本ではこのどちらかを使っている人が多いかなと感じます。

Chainerはもともと習得が簡単なインターフェースで作られている面と、他のフレームワークに比べて、ディープラーニングの開発を論文レベルだったりのカスタマイズをする際に非常に柔軟に対応できるといった点が魅力に感じています。

Define by Runと呼ばれる仕組みがGoogleのTensorFlowをはじめとした他のフレームワークとの大きな違いであり、初心者にとっては、学習途中に数値やサイズの確認が出来るといったデバックの容易さがメリットです（Chainerの開発者から直接聞きました）。
たしかに、学習途中にどのような挙動をしているか、どこでエラーが起きているかは開発者にとっては非常に大事なため、この構造を採用しているのは、大きなメリットだと感じます。

弊社は、このPreferred Networks社のChainerの技術を社会に広めていくための日本で唯一の公認トレーニング企業（2017.07.27現在）であったりします。
また、Microsoft社にともタッグを組み、Chainerによるディープラーニングの実装を、Microsoft Azure上のGPUマシンで高速化するところまで習得できるディープラーニング ハンズオンセミナーも開催しておりますので、よかったらこちらを覗いてみてください。

LSTMで予測してみよう

それでは、RNNの中でよく実装されている**LSTM（Long Short-Term Memory）**と呼ばれる手法を実装していきましょう。
理由は色々とあるのですが、RNNとしてよくLSTMが紹介されていることが多いため、最初のうちはRNN≒LSTMぐらいで覚えておくと良いと思います。

必要なモジュールを読み込もう

Chainerでは色々なモジュールを読み込む必要があり、このあたりは使いながら慣れてくるため、まずはコピペで大丈夫です。
下記で使用しているものは、極力必要最小限に絞っていますので、名前だけでも覚えておくと良いと思います。

import chainer
import chainer.links as L
import chainer.functions as F
from chainer import Chain, Variable, datasets, optimizers
from chainer import report, training
from chainer.training import extensions

LSTMのモデルを定義しよう

Chainerはもちろんのこと、Pythonの使い方にある程度なれていないと最初は難しく感じてしまうものですが、とりあえずL.LSTMの項を入れているため、LSTMが実装できるぐらいの間隔で大丈夫です。

class LSTM(Chain):
    # モデルの構造を明記
    def __init__(self, n_units, n_output):
        super().__init__()
        with self.init_scope():
            self.l1 = L.LSTM(None, n_units) # LSTMの層を追加
            self.l2 = L.Linear(None, n_output)
 
    # LSTM内で保持する値をリセット
    def reset_state(self):
        self.l1.reset_state()
 
    # 損失関数の計算
    def __call__(self, x, t, train=True):
        y = self.predict(x, train)
        loss = F.mean_squared_error(y, t)
        if train:
            report({'loss': loss}, self)
        return loss
 
    # 順伝播の計算
    def predict(self, x, train=False):
        l1 = self.l1(x)
        h2 = self.l2(h1)
        return h2

あとは、Chainerに慣れている方向けですが、LSTMでは内部で状態（State）を保持する構造となっているため、reset_state()を使って、学習のたびに内部の状態で保持している値をリセットする必要があります。
このあたりは、使いながらで大丈夫なので、少しずつ勉強していきましょう。

LSTM用のUpdaterをカスタマイズしよう

ここが一番躓いたポイントで、これを自作するのは難易度が高いです。

Chainerには新しくTrainerと呼ばれる機能が追加され、モデル等の必要な情報を予めセットしておけば、あとはtrainer.run()とすれば、自動的に学習を始め、学習状況の進捗が確認できるといった使いやすい機能が追加されました。
ただ、その分、中が良い意味でブラックボックス化されたため、自力でカスタマイズすることが難しくなりました。

LSTMを使用する際は、最初に書いたreset_state()を実行して、学習ループ毎の状態の値の初期化が必要となるのですが、公式のチュートリアル等に記載されているtraining.StandardUpdaterを使用した場合は、この学習ループごとのreset_state()が実行されず（当たり前ですが）、LSTM系の学習をうまく行うことができません。
Chainerの開発者の方にお尋ねしたところ、以下の２つの方法で解決できると教えていただきました。

• training.StandardUpdaterの更新部分の機能をオーバーライドして自力カスタマイズ
• StatelessなLSTMで書く

後者の方法は内部で保持する変数を自力で書いて渡すため難易度が高く、前者の方法で解決していきます。

training.StandardUpdaterを継承したLSTMupdaterを自作します。
更新部分はupdate_coreに記載されているとのことだったので、こちらの関数をオーバーライドします。

class LSTMUpdater(training.StandardUpdater):
    def __init__(self, data_iter, optimizer, device=None):
        super(LSTMUpdater, self).__init__(data_iter, optimizer, device=None)
        self.device = device
        
    def update_core(self):
        data_iter = self.get_iterator("main")
        optimizer = self.get_optimizer("main")
        
        batch = data_iter.__next__()
        x_batch, y_batch = chainer.dataset.concat_examples(batch, self.device)

        # ↓ ここで reset_state() を実行できるようにしている
        optimizer.target.reset_state()

        # その他は時系列系の更新と同じ
        optimizer.target.cleargrads()
        loss = optimizer.target(x_batch, y_batch)
        loss.backward()
        # 時系列ではunchain_backward()によって計算効率が上がるそう
        loss.unchain_backward()
        optimizer.update()

Chainer用の訓練データと検証データを準備しよう

Chainerで使用するデータセットは、リストもしくはNumpyの形式のデータを準備し、各サンプル毎に、入力と出力でタプルにまとめ、それをリスト化する必要があります。
文章で書くと難しくなりますが、list(zip(..., ...))としてあげればOKです。
なかなかリファレンスが見つからないので、Chainerで使用する独自データセットの作り方を迷われている方もいらっしゃると思いますが、こちらがChainerの開発者の方が推奨する方法です。

# chainer用のデータセットでメモリに乗る程度であれば、list(zip(...))を推奨
# ↑ PFNの開発者推奨の方法
train = list(zip(x_train, t_train))
test  = list(zip(x_test,  t_test))

また、データセットがメモリに乗り切らない（例. 数万枚の画像データ）ようなケースには、ChainerのTupleDatasetを使用すれば、バッチで使用する際のみデータを効率的にメモリに読み込むといった実装がされているそうですので、データサイズが大きくて遅いと感じた場合はこちらをお使いください。

TupleDatasetについて：https://docs.chainer.org/en/stable/reference/datasets.html

Trainerまでの準備

ここまでで、準備が完了のため、以下の流れでTrainerまで設定していきます。

• モデルの宣言：作ったモデルを使う
• optimizerの定義：最適化の手法を選び、モデルと紐付ける
• iteratorsの定義：データセットをバッチ毎に切り分ける
• updaterの定義：更新規則等をまとめる
• trainerの定義：トレーニングの実行に関する設定をまとめる

また、一番最初に以下のコマンドでシードを固定し、再現性の確保を忘れないようにしましょう。
これを忘れると、今日と明日で結果が変わり、明日上司に報告しようとした時に痛い目を見るので注意です。

# 再現性確保
np.random.seed(1)

それでは、上記の流れを一気にいきましょう。

# モデルの宣言
model = LSTM(30, 1)

# optimizerの定義
optimizer = optimizers.Adam()  # 最適化アルゴリズムはAdamを使用
optimizer.setup(model)

# iteratorの定義
batchsize = 20
train_iter = chainer.iterators.SerialIterator(train, batchsize)
test_iter = chainer.iterators.SerialIterator(test, batchsize, repeat=False, shuffle=False)

# updaterの定義
updater = LSTMUpdater(train_iter, optimizer)

# trainerの定義
epoch = 30
trainer = training.Trainer(updater, (epoch, 'epoch'), out='result')
# trainerの拡張機能
trainer.extend(extensions.Evaluator(test_iter, model))　　# 評価データで評価
trainer.extend(extensions.LogReport(trigger=(1, 'epoch')))　　# 学習結果の途中を表示する
# １エポックごとに、trainデータに対するlossと、testデータに対するlossを出力させる
trainer.extend(extensions.PrintReport(['epoch', 'main/loss', 'validation/main/loss', 'elapsed_time']), trigger=(1, 'epoch'))

学習の実行

学習の実行は以下のコマンドで実行がはじまります。

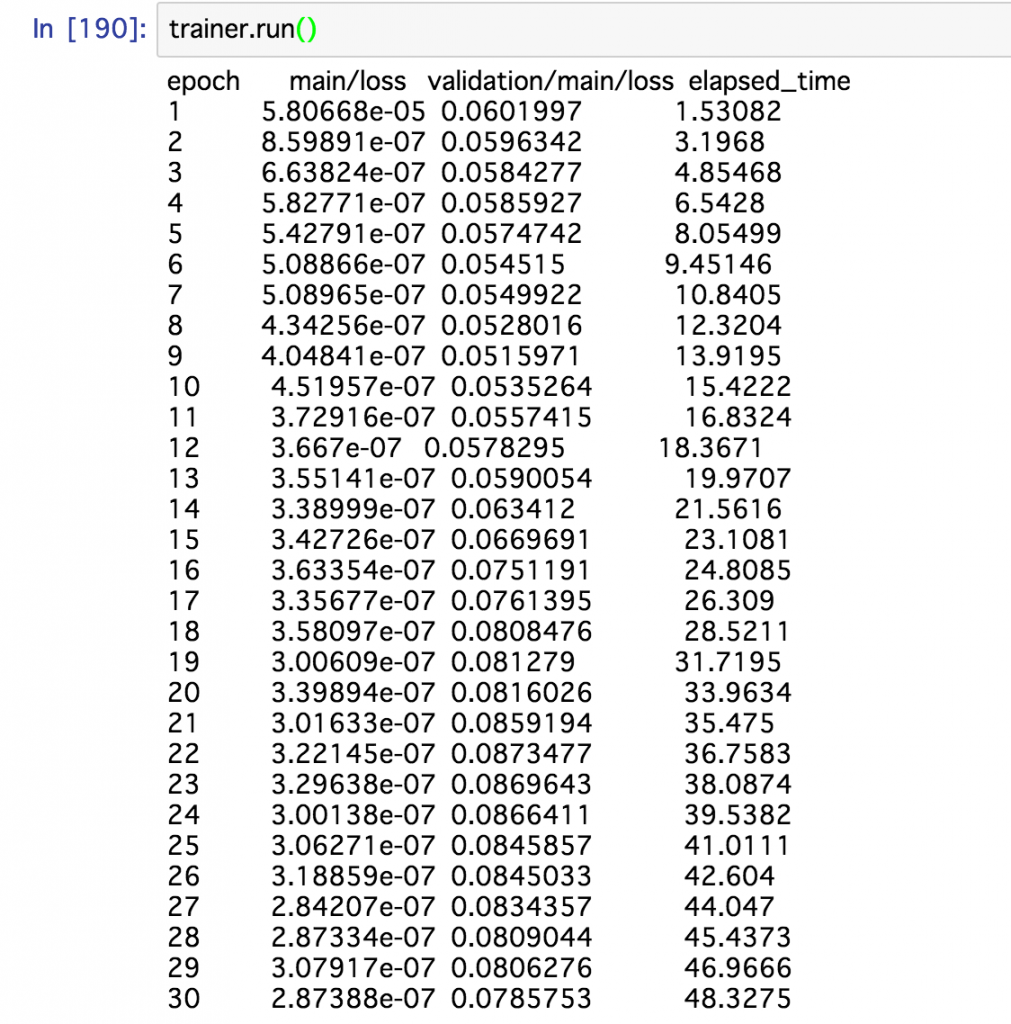
trainer.run()

上記のように、インタラクティブに表示されるため、学習の様子がひと目でわかり非常に便利です。

今回は上記のような学習結果が得られていますが、訓練データに対するlossが下がっていることに対して、検証データに対するlossが下がるどころか、むしろ上がっていたりするので、こういったときはドロップアウトを試そうなど、色々試行錯誤してみてくださいね。

おまけ：ドロップアウトを追加したモデル

ちなみに、ドロップアウトを採用する時は、このようなモデルにするとOKです。

class LSTM(Chain):
    def __init__(self, n_units, n_output):
        super().__init__()
        with self.init_scope():
            self.l1 = L.LSTM(None, n_units)
            self.l2 = L.Linear(None, n_output)
        
    def reset_state(self):
        self.l1.reset_state()
        
    def __call__(self, x, t, train=True):
        y = self.predict(x, train)
        loss = F.mean_squared_error(y, t)
        if train:
            report({'loss': loss}, self)
        return loss
        
    def predict(self, x, train=False):
        # ドロップアウトの追加（訓練時のみ使うようにする）
        if train:
            h1 = F.dropout(self.l1(x), ratio=0.05)
        else:
            h1 = self.l1(x)
        h2 = self.l2(h1)
        return h2

このドロップアウトを追加すると、validationの方のlossも順調に下がっていったため、こういったデータにはオーバーフィッティング（過学習）の対策が必要そうですね。

結果をプロット

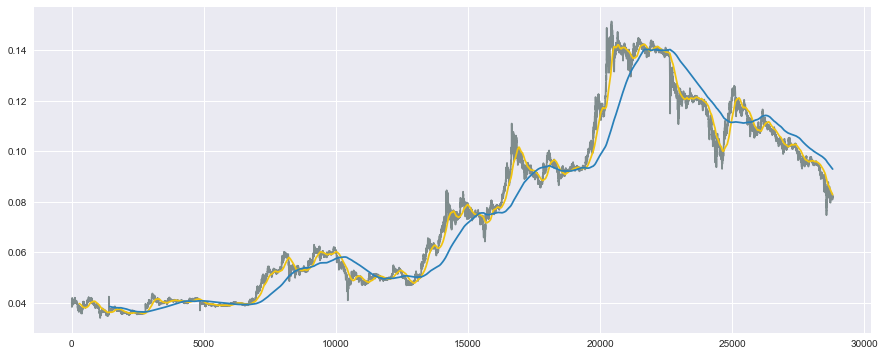
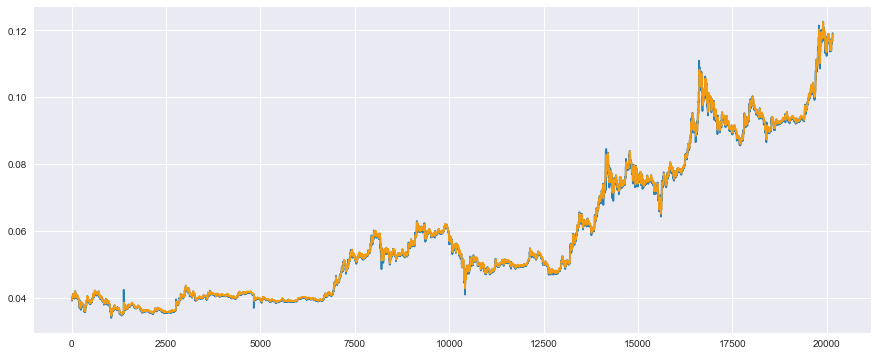
まず訓練データについて見てみましょう。

# 予測値の計算
model.reset_state()
y_train = model.predict(Variable(x_train)).data

# プロット
plt.plot(t_train, color='#2980b9') # 実測値は青色
plt.plot(y_train, color='#f39c12') # 予測値はオレンジ
plt.show()

ある程度うまく予測できていそうですね。

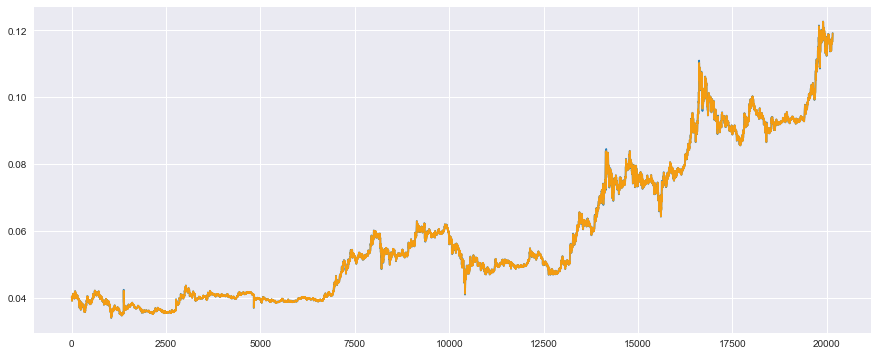
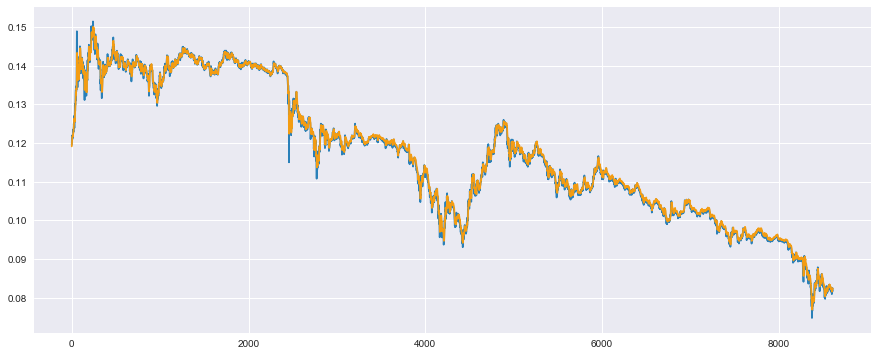
次に、検証データについて見ていきましょう。

# 予測値の計算
model.reset_state()
y_test = model.predict(Variable(x_test)).data

# プロット
plt.plot(t_test, color='#2980b9')  # 実測値は青色
plt.plot(y_test, color='#f39c12')  # 予測値はオレンジ
plt.show()

検証データに対しても、ある程度うまく予測できているようです。
こちらを定量的に評価したいのですが、先ほどの決定係数は時間的なズレがある場合でもかなり良い結果がでるため、あてにならないので、一旦は目視としておきましょう。

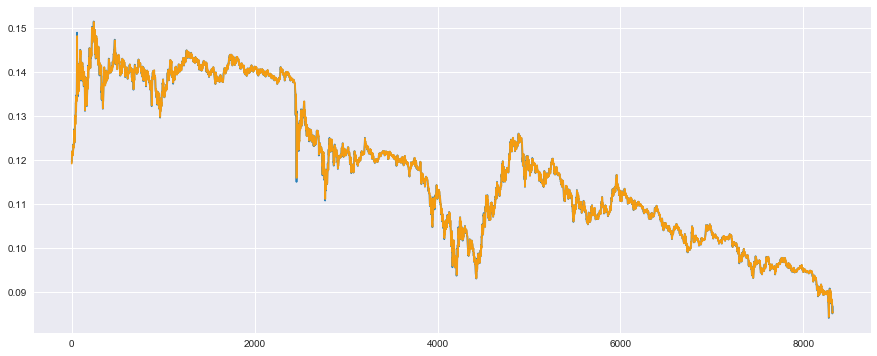
それでは、先ほど純粋にずれていたところを見ていきましょう。

# 検証用の一部を見てみる
plt.plot(t_test, color='#2980b9')  # 実測値は青色
plt.plot(y_test, color='#f39c12')  # 予測値はオレンジ
plt.xlim(200, 300)  # 特徴がわかりやすい一部
plt.show()

なんとなく、前回の重回帰分析よりは単純なずれと言った問題は解決できていそうですね。
ただし、まだ時間的に多少ずれが生じているため、完璧といったところでもありませんね。

今後の展望

今回はまずざっと使ってみようといった部分がゴールであったため、試行錯誤に関しては、これから行っていく予定です。
次のような試行錯誤をまた機会があればご紹介したいなと企画中です。

• 入力変数に該当する仮想通貨以外の価格も考慮する
• 差分や差分の対数といった別の指標も考慮する

本来であれば、ニューラルネットワーク内の特徴量として、後者のような特徴量は自動的に作られるといわれたりしていますが、やはりそこまで理想的な動作はしないようで、人間のノウハウとしてわかっている程度の特徴量であれば、素直に追加した方が良いと言われたりしていますので、このあたりも試してみようかなと。

おわりに

気づくと非常に長文の記事になっていましたが、こういった最初から最後まで通した技術ブログはなかなか無く、個人的には書きたいことをたくさん書けて嬉しいですし、これが読者のみなさんのお役に立てば、なお嬉しいです。

データ解析という言葉は綺麗に聞こえますが、こういったデータを取得したり整形したりと言ったエンジニアリングのノウハウも必要となりますし、ChainerのLSTMを組む際の数学的な考察も必要となります。
幅広い知識をいち早く吸収できるかといった厳しくも楽しい仕事ですので、みなさんもぜひ挑戦してみてください。

フォローお待ちしております

ビジネス目線の機械学習・人工知能の情報やオススメの参考書について発信しています。

株式会社キカガク（公式HP）
代表取締役社長　吉崎 亮介

• Twitter：@yoshizaki_kkgk
• Facebook：@ryosuke.yoshizaki
• Blog：キカガク代表のブログ

最後までお読みいただき、ありがとうございました。