はじめに
今回は指数関数と対数関数をセットで学び直しすることにしました。
学校で習う時、この2つの関数は別々に順次習いますが、学び直しをする時点では両方合わせて勉強した方が理解もより深まると考えました。
また、これらの関数には「底」という概念があり、私にとってはこれが「とっつきにくい」原因になっていました。ですが「ネイピア数 $e$」とあわせて「底が2」、「底が10」、「底がe」などの場合を合わせて考える、より理解が深まりました。
記事の構成
シリーズのパターンに従い、Pythonのコードとメインのコンテンツは以下のGithubページにあります。
またp5.jsを用いたアニメーションなどへのリンクも記事中に貼っています。全てのアニメーションやインターアクティブ・ツール等のインデックスは以下です。
指数関数と対数関数の関係
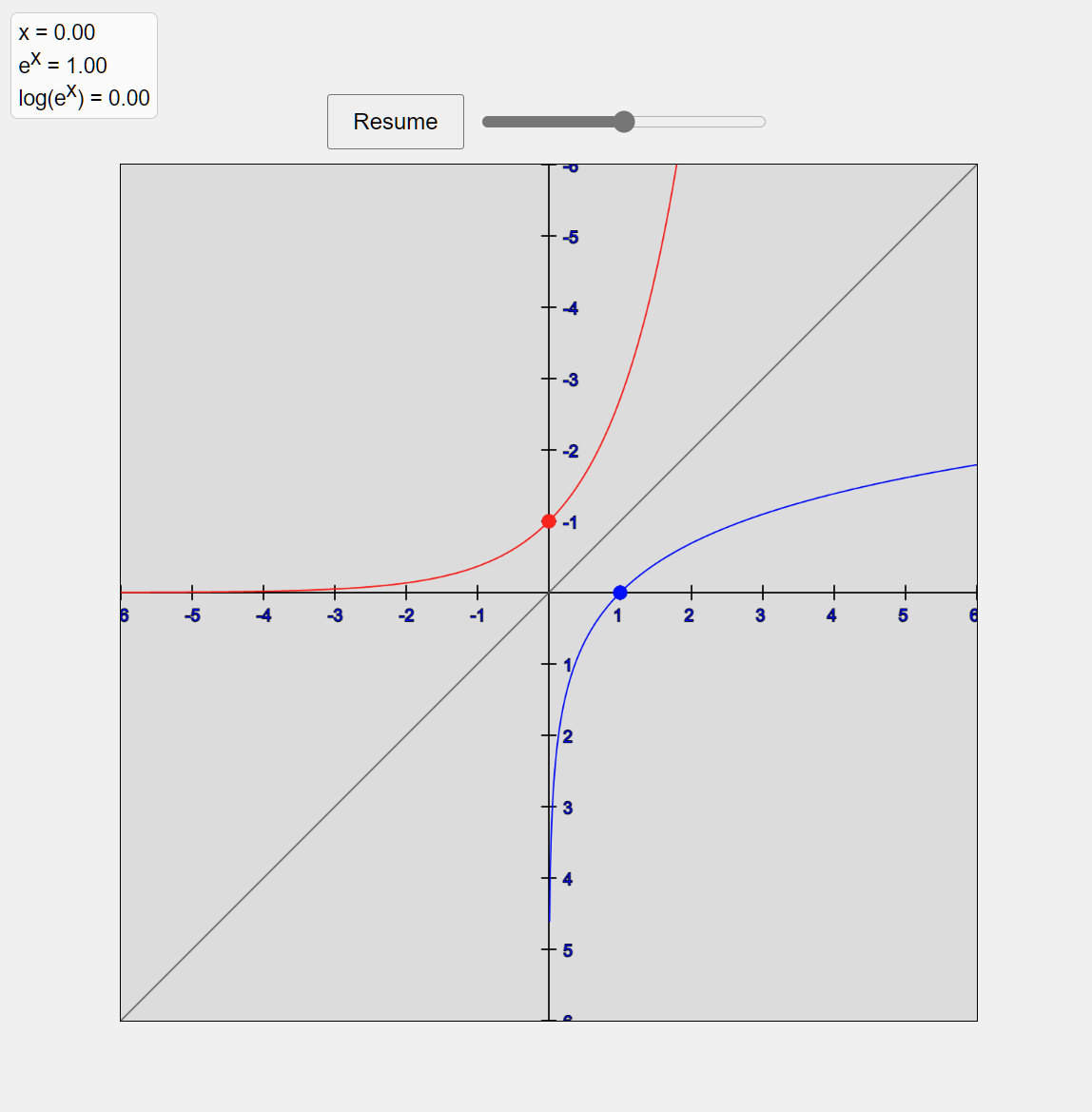
まずはインターアクティブなアニメーションを使ってこ2つの関数が「逆関数」の関係にあることを体験してみましょう。
(以下はプレビューのスクリーンショットです。スクリーンショットの下のリンクからアニメーションのページを開きます)
底が2の指数関数と対数関数
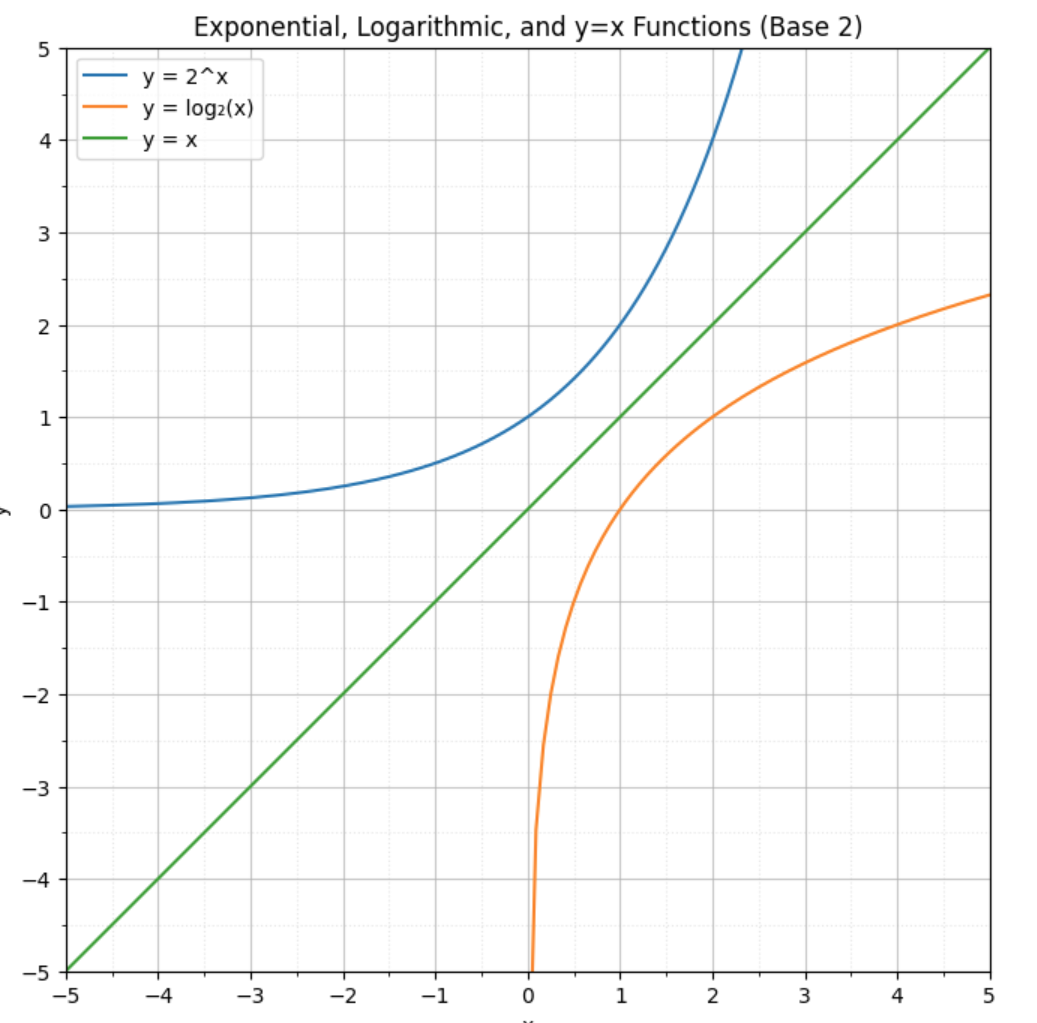
次に、指数関数と対数関数を、プログラミングやソフトウェア開発で馴染みのある2進数の2を底にして見比べてみます。
指数関数(青)は傾きがしだいに急になる様子が分かります。$x=1$の時は$y=2$で、$x=2$の時は$y=4$となり「2の$x$乗」になっているのが分かります。
逆に対数関数(橙)は傾きがしだいに緩やかになっています。$x=1$の時は$y=0$(底2を何乗すれば$1$になるかというと、0乗すればなる)で、$x=4$の時は$y=2$(底2を何乗すれば$4$になるかというと、2乗すればなる)になっているのが分かります。
指数関数と対数関数が逆関数である
指数関数と対数関数をセットで理解するのが効果的な理由は、それらが互いに逆関数になっているからです。別の言葉で言うと、$y=x$に関して対称です。
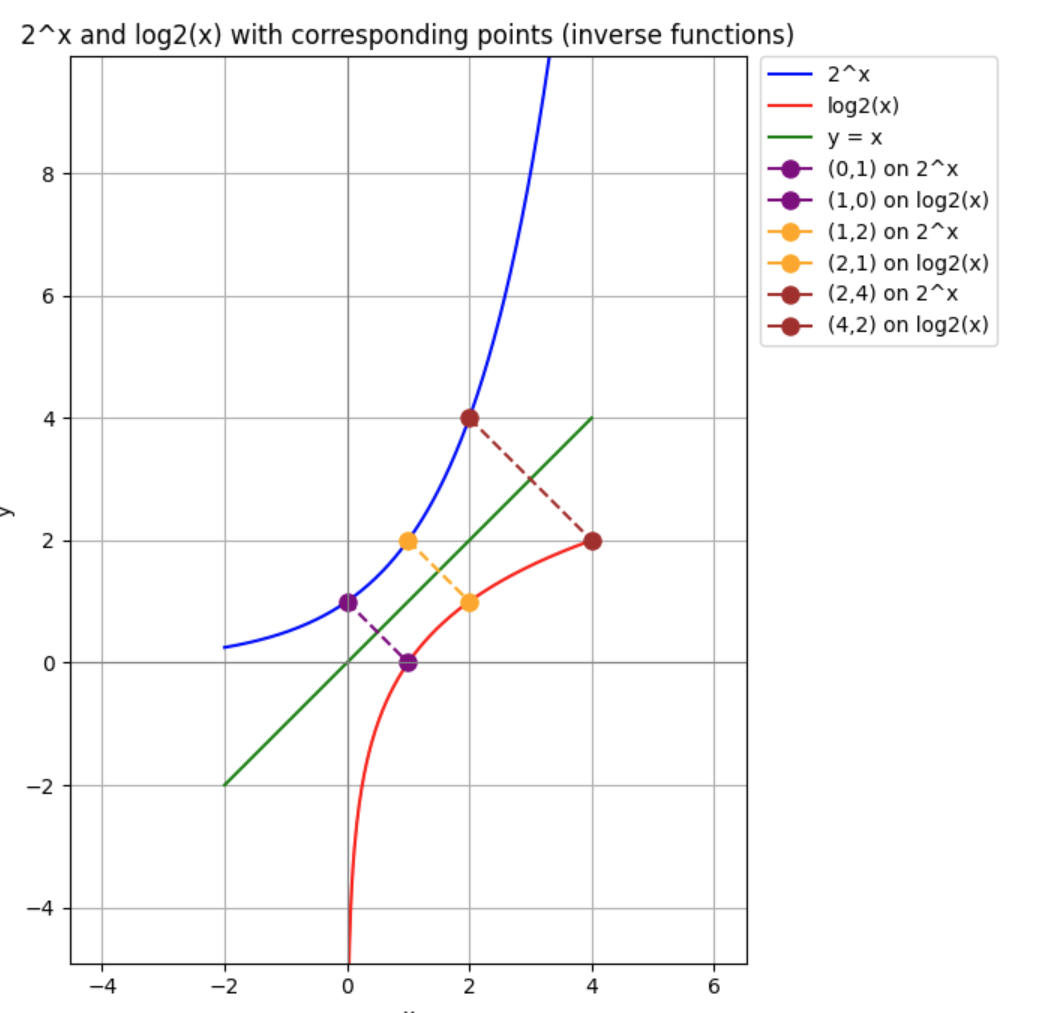
グラフでは座標の$x$と$y$の値をひっくり返した「逆点」が、それぞれの関数のグラフのどの位置にあるかが分かります。
| 色 | 指数関数 $2^x$ | 対数関数 $log_2(x)$ |
|---|---|---|
| 紫 | (0, 1) | (1, 0) |
| 黄 | (1, 2) | (2, 1) |
| エンジ | (2, 4) | (4, 2) |
この3つ点のペアを頭の中のグラフに書くことが出来れば、指数関数と対数関数の大まかな特徴とその関係を把握できたと言えるでしょう。
底が2,10,e(ネイピア数)の場合を比べる
最後に底が異なる時の、2つの関数の違いを見比べてみます。
3つの異なる底の場合の異なる場合に指数関数と対数関数をJavaScriptのインターアクティブページに調べてみましょう。
(以下はプレビューのスクリーンショットです。スクリーンショットの下のリンクからツールを開きます)
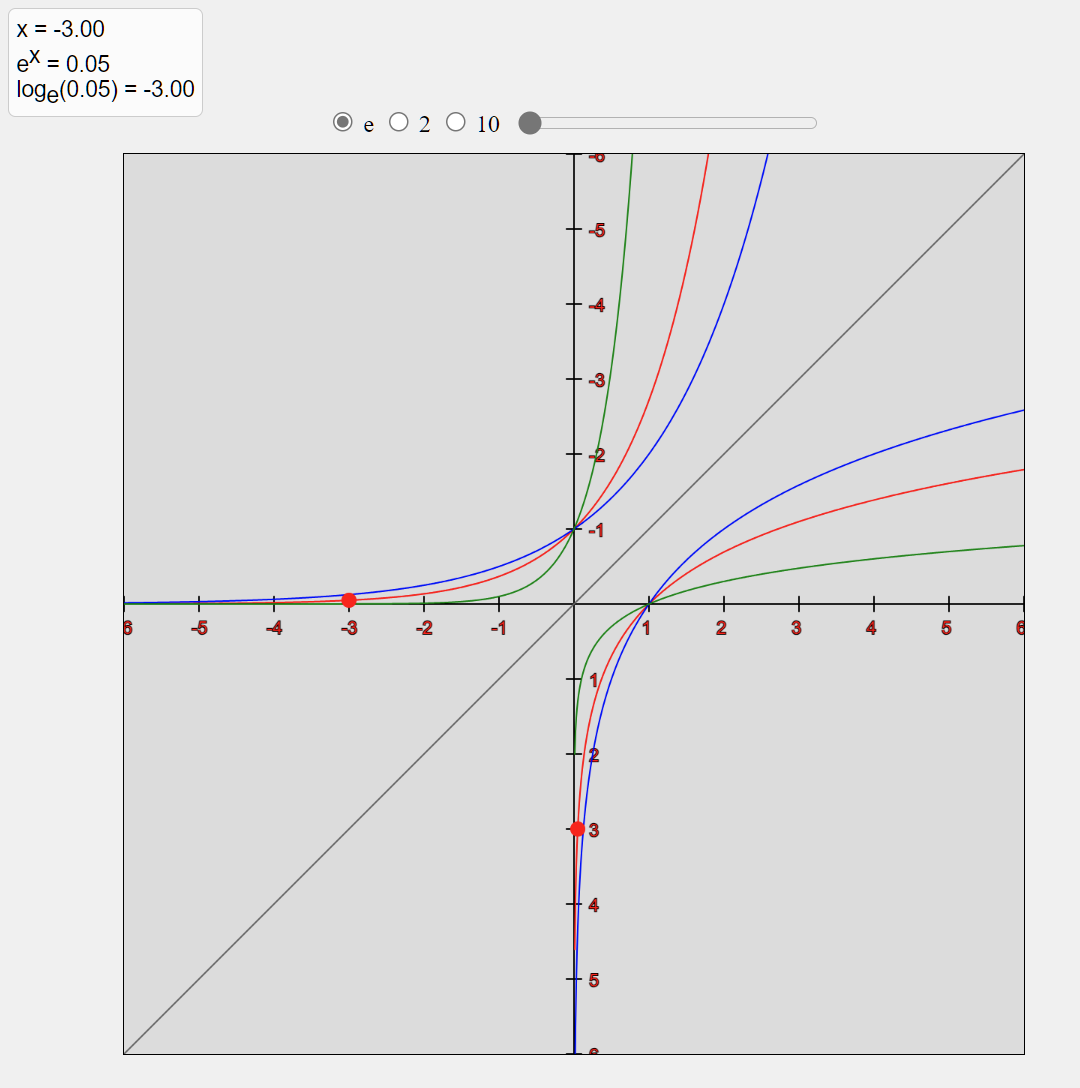
使い方は、まずはラジオボタンを使って「底」を選択し、スライダで点を移動させます(キーボードの矢印キーで微調整できます)
底が大きい10は指数関数と対数関数ともに「緑色」で描かれています。底が小さい2のグラフと比べると、どちらの関数も極端な性質を示しているのが分かります。つまり底の値が大きいほどより極端に増える(対数関数の場合、飽和してします)ことが分かります。
赤色は自然指数と自然対数で、$e$が底の場合です。全ての底の指数関数と対数関数は、ネイピア数を用いた自然対数$ln(x)$で表すことが出来るので、この赤色を標準として底の値の違いを可視化することが出来そうです。