はじめに
これはRetailAI Adventurers Advent Calendar 2023の4日目の記事です.
昨日は@yoshitake_tatsuhiroの記事「形式的意味論ってなんですか?」でした.
主題について,フロントエンド経験0(比喩ではない)の私がダッシュボードを作ることになった際,お世話になったpython製のライブラリであるstreamlitについて書きます.ダッシュボードのようなある程度決まった画面なら,1時間程度でできてしまう優れものです.
記事を書くにあたり,どうせなら自分の役に立つものを作ろうということで,1自由度線形振動系の加振応答を見る画面を作ろうと思いました.質量を持つ物体が,ばねと減衰器で固定されている状態で振動的な外力を作用させたときの物体の振動応答です.streamlitの紹介という主題とは一切関係ありませんが,導出は一応載せておきます.
1自由度線形振動系の加振応答
上記モデルの運動方程式は次式で与えられる.
$$
m \ddot{x} + c \dot{x} + k x = f \cos \Omega t
$$
質量を$m$,ばね定数を$k$,減衰係数$c$である.この式の両辺を$m$で除して次式を得る.
$$
\ddot{x} + 2 \zeta \omega_{n} \dot{x} + \omega_{n}^{2} x = \delta \omega_{n}^{2} \cos \Omega t
$$
ここで,$\omega_n$は固有振動数,$\zeta$は減衰比,$\delta$は静変位を表し,それぞれ次式で与えられる.
$$
\omega_n = \sqrt\frac{k}{m} \qquad \zeta = \frac{c}{2 \sqrt{mk}} \qquad \delta = \frac{f}{k}
$$
両辺を$\delta$で除し,さらに変数$\tau = \Omega t$,$\xi = x/\delta$を導入して置き換えることで次式を得る.
$$
\nu^{2} \xi^{\prime \prime} + 2 \zeta \nu \xi^{\prime} + \xi = \cos \tau
$$
上記方程式の解を,$\xi = \Xi \cos \left( \tau - \phi\right)$で仮定して次式を得る.
$$
\sqrt{\left(1- \nu^{2} \right)^{2} + \left(2 \zeta \nu\right)^{2}} \Xi \cos\left(\tau-\phi+\psi\right) = \cos \tau
$$
左右の項を比較して,解を得る.
$$
\Xi = \frac{1}{\sqrt{\left(1- \nu^{2} \right)^{2} + \left(2 \zeta \nu\right)^{2}}}
\qquad \phi = \psi = \arctan \left(\frac{2 \zeta \nu}{1- \nu^{2}} \right)
$$
環境準備
今回Dockerを使いました.
FROM python:3.10.13-slim-bullseye
RUN apt-get update && apt-get install -y \
build-essential \
curl \
software-properties-common \
git && \
rm -rf /var/lib/apt/lists/* &&\
pip install -U pip && \
pip install streamlit && \
pip install plotly
WORKDIR /src/
EXPOSE 8501
CMD ["/bin/bash"]
早速起動します
docker image build -t streamlit .
docker container run -itd -p 8501:8501 -v ./src:/src --name streamlit streamlit
画面表示
ローカルのsrcディレクトリに,pythonで書いた画面表示のスクリプトを置きます.今回は結果の計算にそこまで時間がかかるものではなかったため,DBは使わずに同じスクリプトの中で計算,表示します.減衰パラメータの変化による応答の違いを見たかったので,スライドバーを加えております.
import streamlit as st
import numpy as np
import pandas as pd
# ページ設定
st.set_page_config(
page_title="ダッシュボード",
layout="wide",
)
# ヘッダ
st.markdown('# 1自由度線形振動系')
# 式
st.latex(r'\sqrt{\left(1- \nu^{2} \right)^{2} + \left(2 \zeta \nu\right)^{2}} \Xi \cos\left(\tau-\phi+\psi\right) = \cos \tau')
# 定義域の指定
xv = np.linspace(0.0,3.0,300)
# 振幅,位相遅れ関数の定義
def amplitude(xv, zeta, delta):
return delta/np.sqrt((1-xv**2)**2+(2*zeta*xv)**2)
def phase(xv, zeta):
return np.arccos((1-xv**2)/np.sqrt((1-xv**2)**2+(2*zeta*xv)**2))
# スライダーの作成
zeta = st.slider('zeta value',0.0,0.5,step=0.01)
yv = amplitude(xv, zeta, 1.0)
pv = phase(xv, zeta)
# データの作成
df = pd.DataFrame()
df['x'] = xv
df['y'] = yv
df['p'] = pv
# グラフ描画
st.line_chart(df, x='x', y='y')
st.line_chart(df, x='x', y='p')
コンテナに入り,streamlitを立ち上げます.
docker container exec -it streamlit /bin/bash
streamlit run vib.py
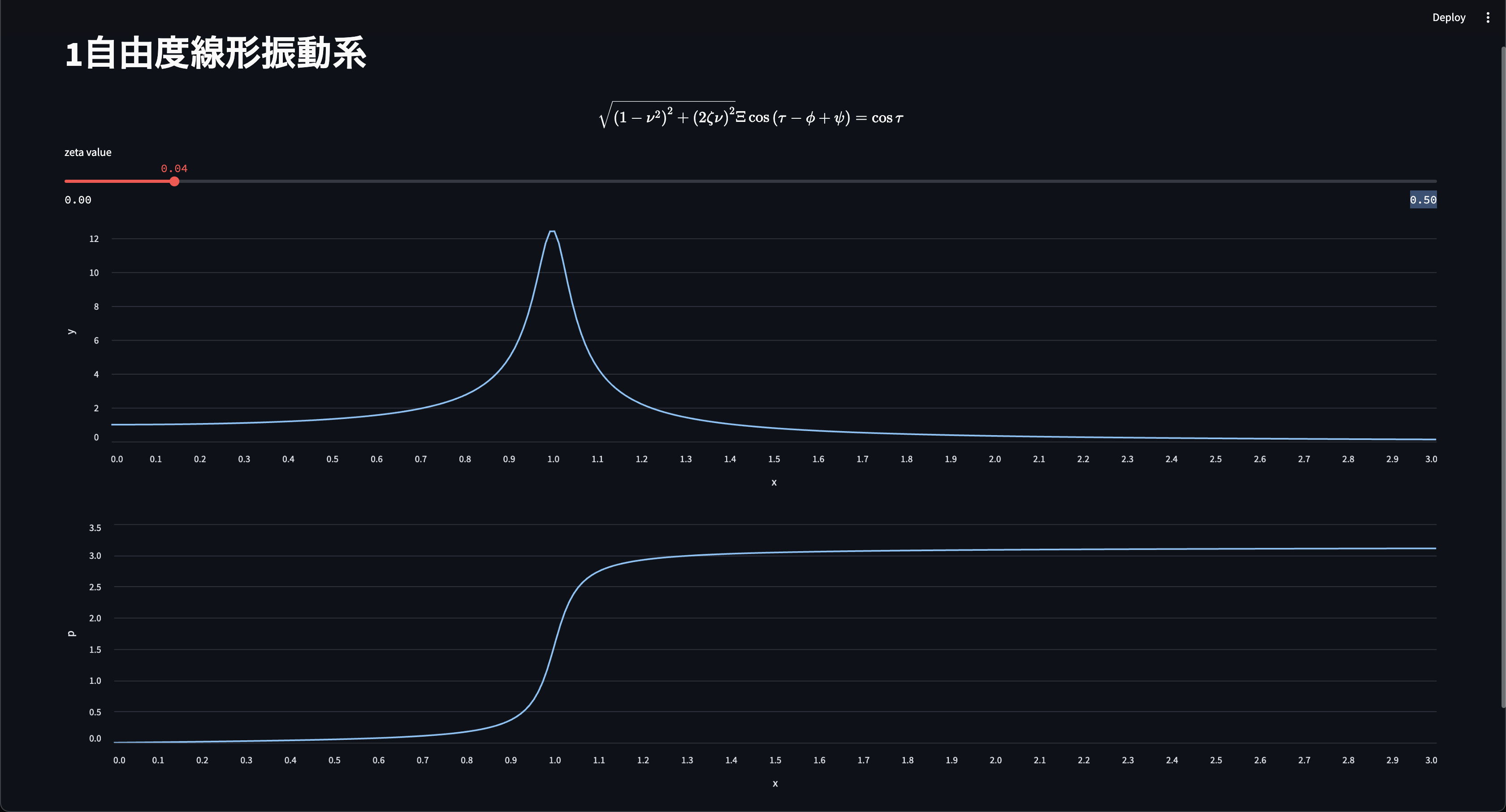
これで完了です.早速http://localhost:8501で見てみましょう.
上の簡易なスクリプトでも,いい感じに体裁を整えてくれています.なにより,問題を導出してから画面表示まで(コンテナの構築含め)30分程度で出来てしまいました.
numpyやpandasといったpythonのライブラリと親和性が高く,データ分析でpythonを使う場合は特に考えることなくstreamlitを使えます.
公式のリファレンスで豊富なサンプルが準備されており,もっと作り込むことは可能です.趣味の範囲であればこれで十分ですね.
閑話休題
個人的に,TeXをすぐにレンダリングしてくれるところが気に入っています.
まとめ
今回はpython製のライブラリstreamlitを紹介しました.コーディングが簡単で,短時間でUIを作れるというのがおすすめポイントです.興味のある方はぜひ使ってみてください.
最後までお読みいただきありがとうございました.明日は,@daisuke-yamamotoさんの担当です.お楽しみに!