はじめに
この記事は,paiza×Qiita記事投稿キャンペーン「プログラミング問題をやってみて書いたコードを投稿しよう!」の中の問題,山折り谷折り (paizaランク A 相当)の解答とそれについての自習の記事である.
この記事を書いている僕は,7月頭に就職してから初めてプログラムに触った人間である.プログラミングの経験は殆どない.大学の一般教養的な授業でCを触った程度である.物理の研究で簡単な解析計算,数値計算にはMathematicaを使っていた.pythonはシミュレーションアプリの中で動いているのを見てちょっと書き換えた程度だ.オブジェクト指向?型?インスタンス?みたいな語を最近知った程度.全く持っての素人が一ヶ月,社内でふらふらpythonの勉強をしたぐらいの実力だ.
キャンペーンに出題されるような問題は,プログラムに明るい人なら苦もなく解ける問題だろう.それをえっちらおっちら解くのがこの記事とキャンペーンの目指すところであろう.みんな鮮やかな解答が見たいというよりは,赤ちゃんがハイハイしているのをみてキャッキャしたいのだと思う.
また,コードや文章に間違いがあれば是非指摘してほしい.
問題:山折り谷折り
この記事で解く問題は,山折り谷折りという問題である.
山折り谷折り
ここで,紙を折る作業は
- 紙を右から左へ谷折りに複数回折る
- 折った紙を全て開く
- 開いた紙の折り目を左から見る
という行為である.この手順で紙を$N$回折って開いたとき,山折りを"1",谷折りを"0"と表記する.
$N$が標準入力として与えられたとき,折り目のパターンを左から"0"と"1"で書かれた文字列として一行で出力せよ.ただし$1\le N \le 20$,$N$は整数.
問題の挙動を見る
こういうのは大抵,非自明な例を数回やると方針が立つ.きっと漸化式が立って,与えられたNに対して数列を求めるか何かするのだろうなと想像できる.
とりあえず,自然数$k$回折って開いたときの折り目を$x(k)$と表す.
では具体的にNに整数を入れて,挙動を見てみよう.
$x(1)$は自明だろう.谷が一つ.よって$x(1)=0$
$x(2)$はリンクの問題文にあるように,$x(2)=001$.
こう書くと,$x(n)$が数字っぽく見えるが文字列だ.$x(2)\neq 1$である.
$x(3)$はすぐにはイメージできない.真面目に紙を折るか.三回折りきって開いていくことを考える.
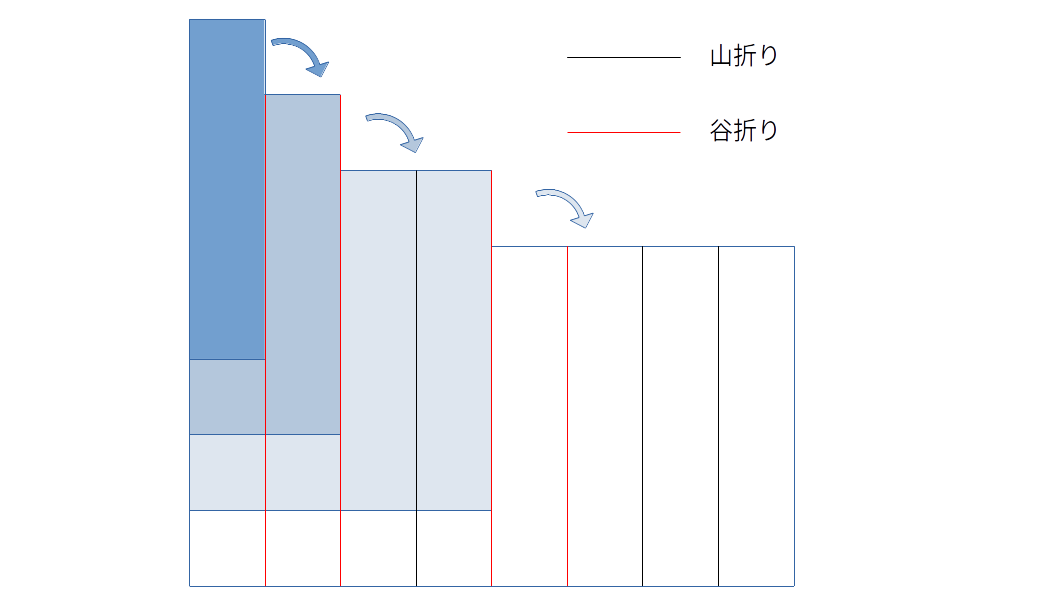
赤が谷折り,黒が山折り.左から読んでいって,$x(3)=0010011$か.
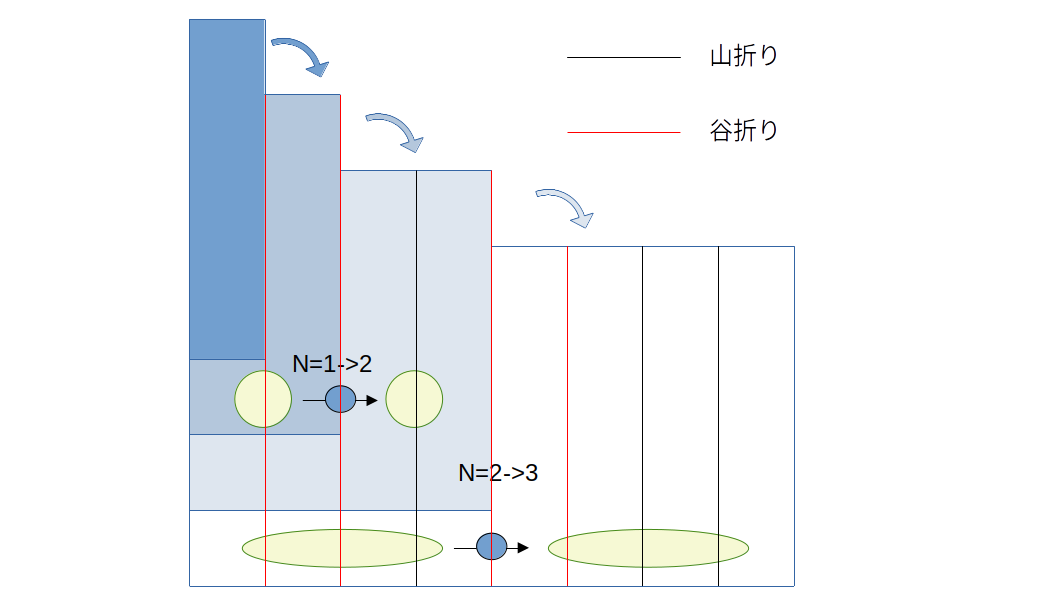
折った紙を開いていくと,なるほどねと気づくことがある.一回紙を開くたびに,自分,0,自分の順序および山谷の反転という折り目が生成されていく.
緑の部分が順序逆かつ山谷反転で展開されていく.青丸のように,反転との間に谷が一つ挟まる.
ということは,$x(k)$と$x(k+1)$の関係は
x(k+1)=x(k)\ 0\ \bar{x}(k)
と書ける.ただし,$\bar{x}(k)$は$x(k)$の順序逆,0,1反転である.
数学的にちゃんとした表記ではないが,とりあえず漸化式のようなものはたった.
解答1:再帰的なアルゴリズム
隣接間の漸化式的なものが立ったので,$x(1)=0$を知った上で再帰的な処理をすれば,任意の自然数$N$に対して$x(N)$が求まる.
プログラムを書くときに,$x(k)$を0,1のリスト形式で持っておいて,出力の直前に文字列にしようと思う.プログラムのことはわからないが,文字列型で持っていると反転とか逆順とかが面倒そうだ.
折り目を作る処理
まずは折り目を作る処理を作ろう.整数を受け取ってリストを返す関数だ.
def make_orime(n):
if n==1:
return [0]
elif n>1:
return make_orime(n-1) + [0]+ [1-x for x in reversed(make_orime(n-1))]
else:
return "Error. Input is not int."
$N=1$のときは初項$x(1)=[0]$を返す.if節の一個目の処理をして,戻り値を返す.
$n \gt 1$の時は$n-1$のときの自分自身,make_orime(n-1) を呼び出す.make_orimeの戻り値はリスト型だ.pythonのリストは"足し算"ができるらしい.
リストの足し算は第一項のリスト末尾に第二項のリストがそのままつながる.
list1=[0,1,2]
list2=[3,4,5]
print(list1+list2)
#[0, 1, 2, 3, 4, 5]
数学的にはどういう扱いになるかはあんまり(僕は)理解してないが.そういう処理らしいから素直に使おうか.
elifの部分はリストの足し算,第三項は逆順$0,1$反転のリストを返している.make_orime(n-1)のリストの要素を逆順に呼び出して1から引いている.リストの要素は0または1だから,1->0,0->1に変換される.
ここの処理はもうちょっとまともになりそうだなぁと思う.$0,1$を反転させるのに引き算を使うのはなんだか意図せぬ挙動がおこりそうで怖い.
噂では,pythonはTrueを$1$,Falseを$0$と同一視するらしいから,0と1でできている各要素をnotで否定するような手段でわかりやすい挙動をするかもしれない.しないかもしれない.なんならわかり易くない挙動な気もする.
下はTrueとFalseが整数型の1と0に対応することを確認している.
print(True==1) #True
print(False==0) #True
deny01=[not 0,not 1] #[Ture,False]
sub01=[1-0,1-1] #[1,0]
deny01==sub01 #True
pythonは異なる型同士(この場合はintとbool)をなんとか比べようとしてくれるようだ.ほかにもflootとintとかもなんとか比べようとしてくれる.親切だなと思う反面,思わぬところで足をすくわれそうで怖い.
閑話休題.elifでの処理は,再帰的に自分自身make_orimeを呼び出す.引数が1ずつ減っていってどこかで条件がTrue,make_orimeの引数が1になって,処理が終わる.
今回の問題設定では,再帰処理が終わらない入力$N$はない.ただし,狂人がとんでもないようなものを入れたときに再帰的処理がおわらなくなるので,一応抜けられるようにelseをつけておいた.
make_orimeの出力は
print(make_orime(3))
#[0, 0, 1, 0, 0, 1, 1]
のようになる.
リストを文字列にする処理
今,make_orimeの戻り値はリストだ.問題で要求されているの出力は文字列だから変換する必要がある.
def list_to_str(list):
return ''.join([str(x) for x in list])
正直にいうと,リストを文字列に変換する方法は(というかだいたい全部の関数,メソッド)は調べて初めて知っている.あんまりjoinなるメソッドがどういうことをしているかわかっていない.ふわっとした理解だと,引数のリストの各要素の間に''を挿入して文字列にしているらしい.
pythonがどういう仕組みで変数なり関数(~オブジェクト?)を持っているかわからないが,なんかこんな処理をしなくても一発でリストの要素の文字列になっていいのではないか?と思う.
list=[0,1,2]
print(list_to_str(list)) #012
ともあれこれでリストを文字列に変換できた.
入力を文字列から整数型にする処理
pythonの入力,input()は文字列型だ.make_orimeの引数は整数だから,それをかえねばならない.
intN=int(input())
int()は整数になるように切り捨てするらしいから,make_orimeで用意した例外は検知されないはずなのかな.
各処理を統合して,入力に対して解答を出力させる
では必要な処理が揃ったからそれらを統合しよう.
intN=int(input())
def make_orime(n):
if n==1:
return [0]
elif n>1:
return make_orime(n-1) + [0] + [1-x for x in reversed(make_orime(n-1))]
def list_to_str(list):
return ''.join([str(x) for x in list])
print(list_to_str(make_orime(intN)))
これが再帰的に解答をもとめるプログラムだ.ターミナル上でyama-tani.pyを実行すれば,入力を求められて,整数を入れれば解答が出力される.
解答2:再帰的にやらないアルゴリズム
再帰的にやるアルゴリズムは直感的にもわかりやすい.ただせっかく問題を解くのだから,単純にといても面白くない.なんとかして別解を生み出したいものだ.解けた問題を解けないことにしてまだまだ悩む.
$N$が与えられたときの$x(N)$がきまっている.$x(N)$の数字の列の左から何番目かを指定したとき,その数字が0,1どちらなのか知れたら行けるのではないか.そういう方針で行ってみよう.
まずは折り紙に帰ってくる.全体で$N$回折るときに,途中$i$回目に折ったときの折り目に注目する.
001001100011011 x(4)
0:1:0:1:0:1:0:1 i=4
0 : 1 : 0 : 1 i=3
0 : 1 i=2
0 i=1
すると,各$i=1,2,3,...$ごとに0101...と並んでいる.
これはよくよく考えれば当然だ.$i-1$回折ってさらにもう一回折るとき,$i$回目にできる折り目は必ず$i-1$回目にできた折り目のすぐ隣にできて,山と谷になる.当然,今まで作ってきた折り目をもう一回折ることはない.常に新しい折り目は直前に作った折り目の両隣にできる.

これから全体で$N$回折ったときにできた折り目のうち,$i$回目に折ってできた折り目を左から数えて$k$番目は0,1,0,1,...と続いていく.
001001100011011 x(4)
1:2:3:4:5:6:7:8 i=4
1 : 2 : 3 : 4 i=3
1 : 2 i=2
1 i=1
上は$N$と$i$を決めたとき$k$がいくつかを書いている.例えば$N=4$,$i=3$なら,$k=1,2,3,4$となる.
今$(N,i,k)$を指定すると折り目を一つ指定できるようになった.この折り目が$x(N)$の左から0,1,2,...(python的な気持ちで0から)数えて何番目にいるかを$a(N,i,k)$で表すことにする.
\begin{align}
a(4,4,1)&=0 \\
a(4,3,1)&=1 \\
a(4,4,2)&=2 \\
& \vdots \\
a(4,4,8)&=14
\end{align}
こうなると,kの値を使って
[x(N)の左からa(N,i,k)番目の数字]=(k+1)\mod 2
と書ける.
具体的な$a(N,i,k)$の表示は
\begin{align}
a(N,i,k)&=2^{N-i}(2k-1)\\ただし,&1\le k\le 2^{i-1},1\le i \le N
\end{align}
となる.同じ$i$をもつ$a(N,i,k)$は$x(N)$でみたときに,$2^{N-i}$個ごとに出てくる.あとは$a(N,i,1)$が何番目に出てくるかを考えれば上の表示が求まる.
方針は立ったので$N$を与えたときに折り目のリストを返すmake_orime2を考える.
まずは$(N,i,k)$を与えたときに$a(N,i,k)$を返す関数は
def retrun_a(N,i,k):
return 2**(N-i) *(2*k-1)-1
となる.ひねりなく表示をpythonで書いただけ.
また,$N$を与えたときの$2^N-1$個の要素をもつリストを作る.
def make_list(N):
return [None for x in range(2**N-1)]
#[None,None,...,None]
Noneは値がない.ただしリストの長さはfor文で回した数だけある.このリストに0,1の値を入れていくことで$x(N)$のリストでの表示になる.
こうして作った空のリストの$a(N,i,k)$番目に値を代入していく.
def make_orime2(N):
tmplist=make_list(N)
for i in range(1,N+1):
for k in range(1,2**(i-1) +1):
tmplist[retrun_a(N,i,k)]=(k+1)%2
return tmplist
tmplist[a(N,i,k)]番目の要素に値を入れるのをfor文のネストでやっている.多分これだと再帰的にやるよりも処理が遅いのだと思う.kについてのfor文は$O(2^N)$回処理をすることになる.
速いかどうかはさておき,再帰的にやらずとも折り目のパターンは求まる.先の解法で作ったinputとoutputを扱える関数を使いまわして,折り目を返すコードは
intN=int(input())
#a(N,i,k)を返す
def retrun_a(N,i,k):
return 2**(N-i) *(2*k-1)-1
#[,,...,] len(...)=2^N-1
def make_list(N):
return [None for x in range(2**N-1)]
def make_orime2(N):
tmplist=make_list(N)
for i in range(1,N+1):
for k in range(1,2**(i-1) +1):
tmplist[retrun_a(N,i,k)]=(k+1)%2
return tmplist
def list_to_str(list):
return ''.join([str(x) for x in list])
print(list_to_str(make_orime2(intN)))
と書ける.
再帰的なアルゴリズムで書いたものよりも,コード全体が長くて,for文が二重になっていて,片方のfor文の処理数は$O(2^N)$だけど,一応別解はできた.
解答3:再帰的にやらない方法の修正
この節は7/31に追記しました.
for文を二重に回しているのが耐えられなかったので,値を入れる部分を修正した.リストを作る部分や出力を文字列にする部分は共通で,make_orime3の部分が新しい.
intN=int(input())
def make_list(N):
return [None for x in range(2**N-1)]
def make_orime3(N):
tmplist=make_list(N)
tmplist[2**(N-1)-1]=0
for i in range(2,N+1):
tmplist[2**(N-i)-1::2**(N-i+1)]=[0,1]*int(
len(tmplist[2**(N-i)-1::2**(N-i+1)])/2
)
return tmplist
def list_to_str(list):
return ''.join([str(x) for x in list])
print(list_to_str(make_orime3(intN)))
解答2と比べてfor文が一重になっている.値の代入をリストのスライスを用いて行っている.
pythonのリストはインデックスを指定して取り出すことができる.スライスと言うらしい.例えば,
testlist=[i for i in range(10)]
print(testlist) #[0,1,2,3,4,5,6,7,8,9]
#seq[start:stop:step] デフォルトは,start=0,stop=len(seq)+1,step=1
print(testlist[::2]) #[0,2,4,6,8]
のように指定のリストから初めと終わり,ステップを指定して抜き出すことができる.上の例はインデックスが偶数(0,2,4,...,8)のものを取り出している.
また,取り出したスライスに値を代入できる.例えばインデックスが偶数の要素に0を代入したいなら
testlist=[i for i in range(10)]
testlist[::2]=[0]*len(testlist[::2])
print(testlist) #[0,1,0,3,0,5,0,7,0,9]
とすれば良い.注意すべきはスライスに代入すると値が変わることだ.この例なら,testlistの要素は変わっている.
また,取り出したスライスに長さが異なるリストを代入することもできるようだ.(試した限りでは)もとのリストで連続する要素のスライスには長さの違うリストを代入できる.
testlist=[i for i in range(10)]
testlist[2:3]=[111,testlist[2],222] #スライスに長さの異なるリストを代入している.
print(testlist) #[0,1,111,2,222,3,4,5,6,7,8,9]
長さの異なるリストの代入ができるのは,python特有の気を利かせてくれるなにかを使っているのだろう.ただ思わぬ挙動をしそうで怖い.
さてもとのmake_orime3を見ていこう.解答2で用意した,$(N,i,k)$を使って議論を進める.紙を全部で$N$回折ったときの$i$回目に折った時の折り目は,左から0,1,0,1,...と続くのだった.全体の折り目の数と同じ長さのリストを用意して,そこに値を入れていく.
$i=1$の折り目は必ず0が入って終わりなので例外的に処理している.
$i\gt1$のところはfor文のところだ.$i$回目に折ったときにできた折り目たちは$a(N,i,k)$から,初項(初めに出てくるインデックス) $2^{N-i}-1$,公差 $2^{N-i+1}$になる.これから取り出してくるべきスライスが指定できる.
取り出してきたスライスと同じ長さの[0,1]を代入してやれば,$i$回目に折ったときにできた折り目の値が決まった.リストに自然数をかけると,その数だけ繰り返したリストになる.$i(\ge 2)$回目に折ったときにできる折り目の数は必ず偶数なので,スライスの長さを2で割ってint()を使わなくてもいいだろう.直接指定してもいいかも知れない.
ともあれこれで$i$についてのfor文を回せばいい.これなら再帰的にやらずに,二重for文も使わずに求める解答がだせる.
おわりに
解けたな.
おそらく出題者側は,再帰的なアルゴリズムによる実装を想像していると思う.アルゴリズム自体はすぐ思いつくものの,python初心者の僕は実装にちょっと苦労した.できる人から見れば大した事のない細々に引っかかった.
初学者が初学者向けに書くのなら,そういう細々した引っかかりを都度書いたほうがいいのだろう.そうは思うが記事の体を保つためにかなり割愛した.そういう細々はすでにqiitaを含むweb上でたくさんの記事が公開されている.あれらよりも価値ある記事はかけそうにない.また,そういう細々を記事にしたければ,もっと難易度の低い問題を記事にすれば良さそうだ.
それでもこの記事を書いたのは,自分自身の成長の足跡を残すためのものである.数ヶ月,数年後の自分が見て拙い文章とコーディングに恥じることになるはずだ.もちろん,いままさにpythonを使い始めている人に初学者から初学者に向けたテキストにも価値があると思う.わかっている人が書いた記事ではわからないものもあるのだ.
最後になるが,別解の作成に関して,概観をつくり多くの議論をしてくれた隣の席のMさん(先輩)に感謝する.他にも初歩的なpythonやプログラミングの質問に丁寧に対応してくれた同輩先輩諸兄に感謝する.