最近数学を勉強し直したほうがいいかなみたいな話を聞くので私もおさらいがてらとりあえず線形回帰(単回帰)をswiftで実装してみたのでメモしておきます。
線形回帰とは
統計学において、Y が連続値の時にデータに Y = f(X) というモデル(「定量的な関係の構造[1]」)を当てはめる事。
回帰で使われる、最も基本的なモデルは Y = AX + B という形式の線形回帰である。
回帰分析 - Wikipedia
たとえば住宅を売るときに、その住宅の敷地面積がどれくらい広ければいくらくらいになるのか推測したりするのに使えます。
いくつかのサンプルデータ(適当です)があるとして、それを表にプロットします。
なんとなく敷地面積が大きければ価格が高くなるような相関が伺えます。

この敷地面積と価格の関係を表すのに y = ax + b という式を利用すると以下のようになります。
価格 = a \times 敷地面積 + b
このデータセットから上の式の a と b を求めるのに最小二乗法というのを使用します。
最小二乗法とは
測定で得られた数値の組を、適当なモデルから想定される1次関数、 対数曲線など特定の関数を用いて近似するときに、想定する関数が測定値に対してよい近似となるように、 残差の二乗和を最小とするような係数を決定する方法、あるいはそのような方法によって近似を行うことである。
最小二乗法 - Wikipedia
先程の表に y = ax + b の線を引いてみます。
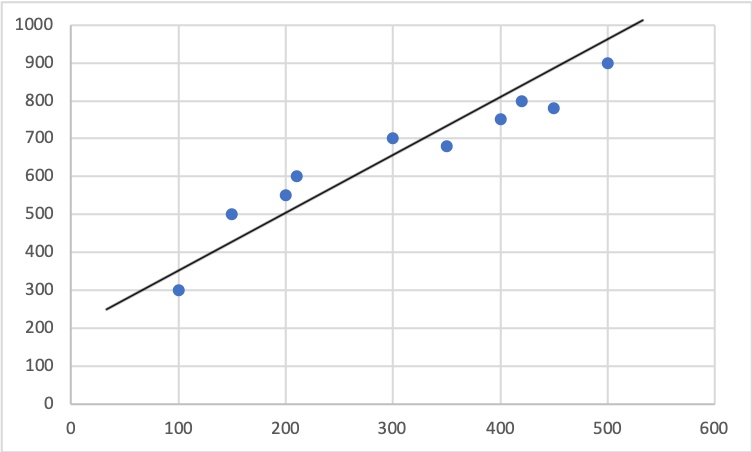
最小二乗法の定義は上に書いてあるとおりですが、図で示すと赤い線(推測された値と実データ間の差)が最小になるような式を求めることになります。

計算式
先程の y = ax + b で a は回帰係数、b は切片となります。
それぞれを求める式は
回帰係数 = \frac{xとyの共分散}{xの分散}\\
切片 = yの平均 - 回帰係数 \times xの平均
共分散と分散って何だっけ…ってなってしまったのでこれもおさらいしておきます。
分散
データの散らばりの度合いを表す数値で「偏差(それぞれの数値と平均値の差)の二乗の平均」で求められます。
\frac{1}{n}\sum_{i=1}^{n} (x_i - \bar{x})^2
共分散
二組の対応するデータの間の関係を表す数値で「xの偏差 × yの偏差 の平均」で求められます。
\frac{1}{n}\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})
これがわかればあとは実装するだけです。
実装してみる
実際のデータを取り込んでとかはめんどくさいので、画面をタップするとプロットされて、それらをデータセットとして最小二乗法により回帰係数と切片を求めて線を描画します。
※ Viewの座標は左上が原点なので左下が原点になるようにy座標は反転します。
それぞれの値の求め方は以下のようになります。
タップされた座標は samples に保持しておくことにします。
var samples: [CGPoint] = []
@IBAction func handleTap(_ tap: UITapGestureRecognizer) {
let location = tap.location(in: view)
samples.append(CGPoint(x: location.x, y: view.frame.height - location.y))
}
let x = samples.map{$0.x}
let y = samples.map{$0.y}
let m = samples.count
// 平均
let plus = { (a: CGFloat, b: CGFloat) -> CGFloat in a + b }
let aveX = x.reduce(0, plus)/CGFloat(m)
let aveY = y.reduce(0, plus)/CGFloat(m)
// XとYの共分散
let sXY = zip(x.map{$0-aveX}, y.map{$0-aveY}).map(*).reduce(0, plus)/CGFloat(m)
// Xの分散
let sX = x.map{pow($0-aveX, 2)}.reduce(0, plus)/CGFloat(m)
// 回帰係数
let a = sXY/sX
// 切片
let b = aveY-a*aveX
以上。
あとは、これらの値を使ってViewに描画すれば完成。
まとめ
昔やったことがあるはずなのですが、結構忘れているものですね…
最小二乗法の計算方法を理解するところが主で、swiftで書いてみる部分に関してはおまけな感じになってしまいましたが、実際に自分で書いてみたことで公式が何をしているのか理解しやすかったです。
どうでも良い話ですが、大学時代に統計学が必須であったのですが、数学選択は難しいクラスで、数学選択以外の人は簡単なクラスにわけられるんですね。
私は数学選択だったのですが、簡単な方のクラスで「サイコロを100回振って実際に1/6の確率になるか試す」みたいな課題が出されていると聞いてそんな簡単な課題があるのかと衝撃を受けたのを思い出しました。
