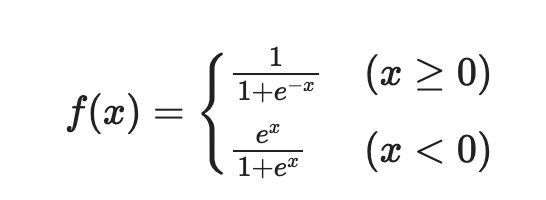シグモイド関数のオーバーフロー対策

Pythonは数値型（整数型や浮動小数点型など）を扱うのが得意で、通常は大きな数値も簡単に扱えます。ただし、指数関数のように急速に増加する値を計算する際には、容易にオーバーフロー（数値が扱える範囲を超えること）が起こることがあります。

では、わざとオーバーフローを起こしてみましょう。

ipynb

import numpy as np

np.exp(1000)

"""出力結果
/opt/anaconda3/lib/python3.7/site-packages/ipykernel_launcher.py:2: RuntimeWarning: overflow encountered in exp
  
inf
"""

このように、$e^{1000}$をPythonに計算させようとするとオーバーフローしてしまいます。この性質に大きく影響してしまうのが、シグモイド関数である。

シグモイド関数は
$$
σ(x) = \frac{1}{1 + e^{-x}}
$$
という風に数式で表された。もし$x$の値が大きな負の値になった時に、先ほどのオーバーフローが発生してしまい計算ができない問題が発生してしまう。シグモイド関数は、ロジスティック回帰やニューラルネットワークの活性化関数で用いられるため、なくてはならない関数であるため、計算できないと非常に困る問題である。

例えば、$x=-100$の場合にシグモイド関数に代入してみると、
$$
σ(-1000) = \frac{1}{1 + e^{1000}}
$$
となってしまいPythonで扱うことができなくなってしまう。

そこで、$x$の値によって関数を場合分けすることで計算できるようにする。

このようにすると$x>=0$の時はを$e^{-x}$計算して$x<0$の場合は$e^x$を計算してくれるため，指数関数の肩の数字がマイナスの値になります。

これでは、指数が大きな負の値になってしまうと思うが、実はPythonは0を返しオーバーフローにはならず計算することができます。

ipynb

import numpy as np
np.exp(-1000)

"""出力結果
0
"""

したがって、$x$の値によって関数を場合分けすることでオーバーフロー対策となり計算ができるようになる訳です。

シグモイド関数を実装するときにこの処理をif文で条件分岐を行なっても良いが、以下のように１行で返り値を書くことができる。

ipynb

import numpy as np

def sigmoid(x):
    return np.exp(np.minimum(x, 0)) / (1 + np.exp(- np.abs(x)))

np.minimum(x_1, x_2)では、引数に指定した値で小さい方を用いることができるので$x$が0より小さい時だけ$x$の値が使われる状態となる。そして、0が選択されたときは内部的にnp.exp(0)となり数式的に$e^0=1$となり、分子が1として成り立つ。