前回の記事では試行的にテンソルネットワーク (MPS) でベイジアンネットワークを表現しました。
本記事では MPS を量子回路に置き換えることによって、ベイジアンネットワークをより浅い量子回路で表現します。量子回路への変換方法については文献 [1] を参考にしました。
ただし、ここで実験した方法では、MPS を完全に量子回路に置き換えることはできず、実機で動かすことも困難という問題があります。
それでも、テンソルネットワークと量子コンピュータの間の関係が見えてくると思います。
元のテンソルネットワーク
前回使用したテンソルネットワークの形式について振り返ります。
上部にある 4 つの矢印 (x1,x2,x3,x4) が入力を、下部にある 1 つの矢印 f(x) が出力を表します。
赤線部分のボンド次元が 2 の場合には、機械的にユニタリ演算子に置き換えることができます。
(以降、ボンド次元 2 を前提とします)

量子回路への置き換え手順
MPS から量子回路への置き換えは機械的に行うことができます。
- 入出力をケットベクトルに置き換える
- 前回と同様のテンソルネットワーク変形によって特異値を D の位置に移動させる(図の左)
- さらに特異値分解を行い、図のように特異値と出力部分を右に追加して ΣV とする(図の右)

- A を 1 量子ビットゲートに置き換える
- B,C,D を 2 量子ビットゲートに置き換える(出力の一方は |0⟩ に固定)
- D の出力を観測する
- 残った ΣV はユニタリ演算子で表現できないので、古典的に計算する
最後の部分で古典計算が必要になるため、この方法では MPS を完全に量子回路に置き換えたことにはなりません。
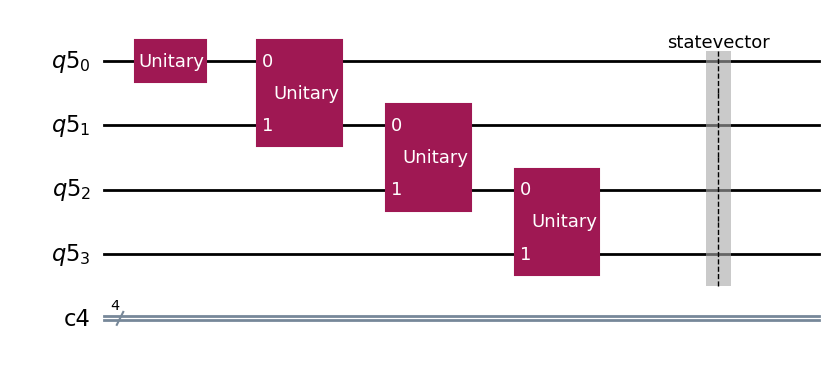
テンソル A,B,C,D をそれぞれ量子ゲート U1,U2,U3,U4 で置き換えたとすると、量子回路は下の図のようになります。

- テンソル A,B,C,D からなる配列 matrices について特異値分解を行い、ΣV を返す関数を次のように実装します。
import numpy as np
def normalize_mps(matrices):
# テンソルA
U, s, V = np.linalg.svd(matrices[0], full_matrices=False)
matrices[0] = U
matrices[1] = np.einsum('ij,jkl->ikl', np.diag(s) @ V, matrices[1])
# テンソル B,C,D
for i in range(1, len(matrices)):
m = matrices[i]
m = m.reshape([2*m.shape[0], m.shape[2]])
U, s, V = np.linalg.svd(m, full_matrices=False)
s = np.diag(s)
matrices[i] = U.reshape(matrices[i].shape)
if i < len(matrices) - 1:
matrices[i+1] = np.einsum('ij,jkl->ikl', s @ V, matrices[i+1])
return s @ V
A の変換方法
テンソル $A$ は特異値分解を行った時点でユニタリ行列になっているため、そのまま量子ゲート $U_1$ になります。
B, C, D の変換方法
テンソル $B^j_{ik}$ はインデックス $i, j, k$ がバイナリになっているテンソルで、8 個の値を持っています。
これをユニタリ表列 $U_2$ に変換します。

まず、添字の位置に注意しながら 8 個の値を表のように配置して、新たな $2 \times 4$ 行列 $X$ を作ります。
その後、$X$ のカーネル ($\mathrm{Ker} X$) の基底を求めて、それを 2, 4 行目に追加することで、$\mathrm{rank}$ $2$ のユニタリ行列を作ることができます。これが $U_2$ になります。
| 00 | 01 | 10 | 11 |
|---|---|---|---|
| $B^0_{00}$ | $B^1_{00}$ | $B^0_{10}$ | $B^1_{10}$ |
| $B^0_{01}$ | $B^1_{01}$ | $B^0_{11}$ | $B^1_{11}$ |
$X$ の 1 行目は出力 $k$ が $|0\rangle$ になるときの入力の分布、2 行目は出力 $k$ が $|1\rangle$ になるときの入力の分布になっています。また、$X$ の各列は入力のインデックス $i, j$ を表しています。
$B$ を $U_2$ に変換する関数を次のように実装します。$C, D$ もこの関数で変換できます。
from scipy.linalg import null_space
# tensorの添字は tensor[j][i][k] の順序
def get_unitary_op(tensor):
U = np.zeros([tensor.shape[2], tensor.shape[0]*tensor.shape[1]])
for (i,j,k) in [(i,j,k) for i in range(tensor.shape[0]) for j in range(tensor.shape[1]) for k in range(tensor.shape[2])]:
U[k, j*2+i] = tensor[i,j,k]
kernU = null_space(U)
return np.array([U[0], kernU.T[0], U[1], kernU.T[1]])
量子回路シミュレータで計算
量子回路を実装する準備ができたので、ベイジアンネットワークを qiskit の量子回路シミュレータで計算します。ベイジアンネットワークを(近似的に)MPS で表現できている状態から始めます。
ここでは MPS を定数で設定してしまいます。
mps = []
mps.append(np.array([[-0.96414437, -0.26537828], [-0.26537828, 0.96414437]]))
mps.append(np.array([[[-0.55841113, 0.27210687], [-0.82144954, -0.18497485]],
[[0.0978425, -0.5045371], [-0.06184265, -0.79823836]]]))
mps.append(np.array([[[-0.61909484, 0.44758962], [-0.62551758, -0.27409111]],
[[0.36071979, -0.36521617], [0.30875648, 0.76886588]]]))
mps.append(np.array([[[-0.69009564, 0.17513174], [-0.7223939, -0.14502367]],
[[0.03635054, 0.8075315], [-0.02436595, 0.54423331]]]))
sigmaV = np.array([[2.34089487, 2.96663868], [-1.02656386, 0.81003395]])
MPS をユニタリ行列に変換します。
unitaries = [mps[0]]
for i in range(1, len(mps)):
unitaries.append(get_unitary_op(mps[i]))
量子回路を構築します。
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit_aer import AerSimulator
from qiskit.circuit.library import UnitaryGate
q = QuantumRegister(4)
c = ClassicalRegister(4)
circ = QuantumCircuit(q, c)
g1 = UnitaryGate(unitaries[0])
circ.append(g1, [0])
g2 = UnitaryGate(unitaries[1])
circ.append(g2, [0, 1])
g3 = UnitaryGate(unitaries[2])
circ.append(g3, [1, 2])
g4 = UnitaryGate(unitaries[3])
circ.append(g4, [2, 3])
circ.save_statevector()
circ.draw('mpl')
検証可能にするために、ステートベクトルを直接参照します。
backend_sim = AerSimulator()
backend_sim.set_option('method', 'statevector')
result = backend_sim.run(circ).result()
statevec = result.get_statevector()
print(statevec)
Statevector([ 0.2609447 +0.j, 0.31955621+0.j, 0.18339716+0.j, 0.39298557+0.j, 0.31819723+0.j, 0.38287479+0.j, 0.19022988+0.j, 0.46688262+0.j, 0.15942316+0.j, 0.16723119+0.j, -0.02563803+0.j, 0.18929075+0.j, -0.11728279+0.j, -0.12496128+0.j, 0.00934952+0.j, -0.14276504+0.j], dims=(2, 2, 2, 2))
観測する量子ビット以外の 3 個の量子ビットの出力は $|0\rangle$ 固定のため、実際に $|0\rangle$ になっている部分のみ着目します。
result = np.array([statevec[0], statevec[8]])
print(result)
[0.2609447 +0.j 0.15942316+0.j]
最後に $\Sigma V$ を古典的に計算して結果を得ます。
out = np.einsum('i,ij->j', result, sigmaV)
print(out**2)
[0.19997536+0.j 0.81589091+0.j]
前回の記事で入力を $(0, 0, 0, 0)$ としたときの結果と一致しました。
もちろん、各量子ビットに $X$ ゲートを追加することで、他の入力に対する結果を計算することもできます。
おわりに
本記事ではボンド次元が 2 の MPS を量子回路シミュレータで扱えることを確認しました。
しかし、冒頭で触れた問題以外にも以下のような問題があります。
- ボンド次元 2 で充分な精度で近似できるデータは限られる。
- 正の実数しか使っていないので、干渉などの量子の強みを活用できていない。
実用を考慮すると近似精度が大きな問題になってくるので、今後テンソルネットワークの表現についてさらに追求していきたいと思います。
参考文献
[1]: Shi-Ju Ran. Encoding of matrix product states into quantum circuits of one- and two-qubit gates. Phys. Rev. A 101, 032310