Project Euler 58「螺旋素数」

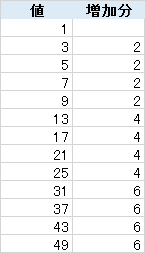
いつものようにジーッと眺めて法則性を探す。

Problem 58 「螺旋素数」

1から始めて, 以下のように反時計回りに数字を並べていくと, 辺の長さが7の渦巻きが形成される.

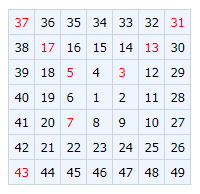
面白いことに, 奇平方数が右下の対角線上に出現する. もっと面白いことには, 対角線上の13個の数字のうち, 8個が素数である. ここで割合は8/13 ≒ 62%である.
渦巻きに新しい層を付け加えよう. すると辺の長さが9の渦巻きが出来る. 以下, この操作を繰り返していく. 対角線上の素数の割合が10%未満に落ちる最初の辺の長さを求めよ

def hoge(num):
    ratio = {True: 0, False: 1}
    n, m = 1, 2
    while True:
        for _ in range(4):
            n += m
            ratio[is_prime(n)] += 1
        if ratio[True] / sum(ratio.values()) * 100 < num:
            break
        m += 2
    return int(n ** 0.5)

def is_prime(n):
    if n < 2: return False
    if n == 2: return True
    if n % 2 == 0: return False
    return all(n % i != 0 for i in range(3, int(n ** 0.5) + 1, 2))

print(hoge(10))

法則性