皆さん,MATLABしてますか??研究で趣味で,MATLABはとっても良いツールですよね! 変数のインデックスが1から始まるところ以外は.
こんなに素晴らしいMATLABは,就活にだって存分にその能力を発揮できちゃうんです!
実際に,私の就活のときに役に立った例をご紹介します.
問題例
以下に示すのは,あるテーマパークの来場者数と飲料の販売量に関するデータである.7月における飲料の販売量を概算せよ.
| 来場者数 [千人] | 最高気温 [度] | 最低気温 [度] | 飲料の販売量 [l] | |
|---|---|---|---|---|
| 4月 | 402 | 23.8 | 6.3 | 260.5 |
| 5月 | 492 | 31.6 | 11.2 | 325 |
| 6月 | 286 | 33.0 | 17.7 | 225.5 |
| 7月 | 195 | 35.6 | 20.1 | ? |
| (上記のデータは架空のものです) |
どこの会社の就活だったかは忘れました.
ただ,世界にその名を轟かせる超大企業のどこかだったと思います.
この会社は,こんな問題をバンバン出して来て,MATLABで解いてもギリギリの時間配分でした.とても手計算じゃ間に合わない.むしろこうすることで,計算ツールを使いこなせる人間だけを抽出しようとしている可能性があると感じました.
解き方
テキトーに仮説を立て,方程式を作ります.
今回は,飲料の販売量が来場者と最高気温と最低気温の関数になっているという仮説を立て,来場者をx,最高気温をy,最低気温をz,飲料の販売量をkとして, ax+by+cz=k と方程式を作りました.4月の場合をあてはめると, 402a + 23.8b + 6.3c = 260.5 になります.ここで,明らかになっている4,5,6月の販売データから,a,b,cの係数を算出できれば,7月の飲料の販売量も算出できるはずです.
さて,4,5,6月の方程式を並べると,以下の行列式ができます.
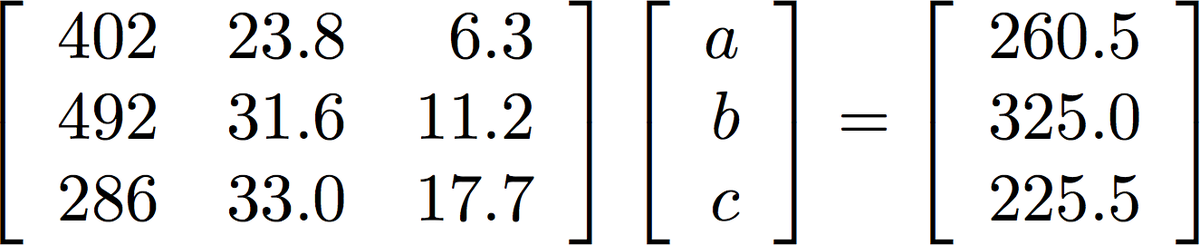
線形代数でやったような気がしますね.左端の大きな行列をA,abcの行列をx,右端の行列をbと置くと, Ax=bとなり,xを求める場合には,両辺に A^-1 を前からかけて, A^-1 Ax = A^-1 b として, x = A^-1 b とすることで,Aの逆行列とbのかけ算の形にして解くんでした.

MATLABによる回答例
まず,以下のようにAとbの行列を入力します.
>> A = [[402 23.8 6.3];[492 31.6 11.2];[286 33.0 17.7]]
A =
402.0000 23.8000 6.3000
492.0000 31.6000 11.2000
286.0000 33.0000 17.7000
>> b = [260.5;325;225.5;231.5]
b =
260.5000
325.0000
225.5000
そして, x = A^-1 b は, A\bと入力します.すると,a,b,cに対応した係数が計算できます.
>> A\b
ans =
0.5000
2.5000
0.0000
計算結果は以上のようになり,来場者数の0.5倍と最高気温の2.5倍と関係した係数が算出されました.結果によると,最低気温については,飲料の販売数とは全く関係しないということが分かりました.この係数を使用すると,7月の飲料の販売数は, 1950.5 + 35.62.5 + 20.1*0.0 で,186.5と試算できます.