単回帰分析から一つづつレベルを上げることでベイズ回帰モデル, 深層学習, 更に深層ベイズに至るまでにどのように繋がているのかについて簡単に解説します. 普段は python の実装を加えますが今回は数式のみを使って解説するので恒久的な内容になります.
もし誤りがあればご指摘よろしくおねがいします.
回帰モデルの定義をここでは
「説明変数 $x$ をインプットとして連続値の目的変数 $y$ を説明するモデルを観測データから作成すること」
とします. つまり観測データを十分に説明できる
y = f(x)
という具体的な関数$f(\cdot)$を求める事ができれば回帰モデルができたとします.
ここでは
- $x$ 説明変数
- $y$ 目的変数
- データを識別する添字を $i = 1,\cdots, N$
- 観測されたデータ $D = (x_{i},y_{i})$
とします.
レベル1:線形単回帰
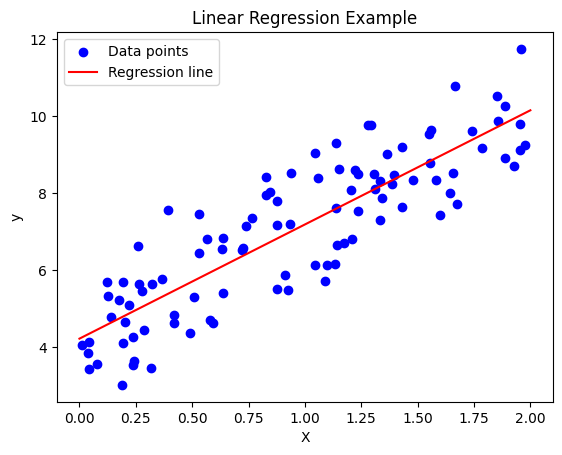
もっとも初歩的で簡単な回帰モデルは $y$ と $x$ の関係を一次関数で回帰するモデルです. このモデルは線形単回帰と呼ばれます.
y =f(x) = ax + b
この場合パラメータ $(a,b)$ を求めることで回帰モデルを作成できたとします. $a$ は傾き, 切片 $b$ はバイアスパラメータと呼ばれます. 単回帰分析は $(x,y)$ の関係を直線で表しこの直線を回帰直線と呼びます.
パラメータを求めるためによく使われるのは最小二乗法を利用する方法で, これは $y-f(x)$ の差分の大きさが小さくなれば観測データをうまく説明できる回帰モデルができるだろうという考え方です.
最小二乗法
すべての観測データ$D$の誤差の二乗和
E = \sum_{i=1}^{N} (y_{i} - (ax_{i}+b))^{2}
を最も小さくする$(a,b)$を求めます. これが最小二乗法と呼ばれる方法で, $E$をモデルのパラメータ$(a,b)$で偏微分して極値を求めれば解が得られます. また, パラメータについて一般解が知られており, 大抵の教科書に書いているのでここでは省略します.
レベル2: 確率モデル
レベルアップ: $y$ を確率変数に格上げする
一般の測定には偶然誤差と呼ばれる確率的に発生する誤差が含まれます. $(x,y)$ の関係に偶然誤差を考慮したモデルが次の確率変数 $\epsilon$ を含んだ回帰式で
y = ax + b +\epsilon
というモデルを考えます. ここで重要なのは確率変数 $\epsilon$ を加えることで観測値 $y$ も確率変数に格上げされていることです. (確率変数+定数=確率変数であることに注意)
確率変数 $\epsilon$ として最もよく使われるのは, 平均が0で分散が $\sigma^2$ のガウス分布, $\epsilon \sim N(0,\sigma)$,に従う場合です. (必ずしもガウス分布に従う必要があるわけではないです.)
ガウス分布に定数を足した確率変数もまたガウス分布に従うという事実から $y$ もまたガウス分布に従い,平均と分散は
E[y] = ax + b ,
V[y] = \sigma^{2}
であるため $y \sim \mathcal{N}(ax + b, \sigma^{2})$ というガウス分布に従うことがわかります.
最尤推定法
$y$を確率変数に格上げしたことでパラメータ$(a,b)$を求める方法の幅が広がり, 最尤推定法が使えます.
まず
- $\boldsymbol{w}$: をモデルのパラメータをまとめた表記とします.
- $p(y|x,\boldsymbol{w})$ を確率モデル とします.
最尤推定法は
L = \prod_{i=1}^{N} p(y_{i}|x_{i},a,b,\sigma)
で定義される尤度関数を最大にする $(a,b,\sigma)$ が現象を最もよく説明できるモデルのパラメータであるという考えから得られる手法です.
それぞれの観測データは確率モデルの分布に従って得られる 独立事象 であるため $p(y_{i}|x_{i},a,b,\sigma)$ の積である尤度関数はデータ $D$ が得られた確率であると解釈できます.
つまり, 尤度関数 $L$ が最大となるときにデータ $D$ が観測される確率は最大であり, そのようなモデルパラメータ $(a,b,\sigma)$ が現象を最もよく説明しているという思想です.
ただし,
- 数式上の使いやすさ
- 数値計算において尤度は非常に小さな値になる
のため, よく利用されるのは対数尤度 $l = \log L$ であり, 対数尤度を最大化する $(a,b,\sigma)$ を計算されます. 対数尤度を最大にする $(a,b,\sigma)$ を求めるには $l$ をそれぞれのパラメーターで偏微分して極値を計算すればできます.
この方法は $\epsilon$ がどのような確率変数であっても使える方法です.
確率モデルから点推定へ
最尤推定を用いて $(a,b,\sigma)$ を決めたとしても, 実は回帰問題は解けていることにはなりません.
なぜならば, $(x,y)$ の関係が $y \sim \mathcal{N}(ax + b, \sigma^{2})$ という確率分布に従っている事がわかっただけで $y=f(x)$ の形で 新しいデータ $x^{}$ に対して決定的に $y^{}$ の値を予測できていないからです.
このように $x$ の値に対して確率変数 $y$ がどのような値を取りうるかを「確率を除外して」一意に決めることを $y$ についての決定論と呼びます. 最も多く用いられる決定論は期待値をそのまま $f(x)$ とすることです.
y^{*} = f(x^{*}) = E[y^{*}]
ガウス分布を利用した場合 $f(x) = E[y] = ax + b$ で与えられ線形単回帰モデルと同じ結果がえられますが, 観測データの偶然誤差とその分散についても考慮しているため線形単回帰よりもレベルが上がっていると解釈できます.
注意
ここで一つ重要なポイントです. 実は $\epsilon$ をガウス分布に従うと仮定した場合の最尤推定法と単回帰分析における最小二乗法で求めるパラメータ $(a,b)$ の結果は同じになります. ガウス分布の対数尤度関数がパラメータの2次に依存しているためです. 逆に最小二乗法を使っているときには偶然誤差としてガウス分布を利用していると考えて問題ないです. (分散を推定しているかどうかの違いはあります)
レベル3:線形重回帰
レベルアップ: $y$ を説明するパラメーターを増やす
レベル2の確率的線形回帰モデルをより一般化して, モデルのパラメータを増やしてみましょう. 説明変数を増やせばそれだけ事象を説明しやすくなります. $x_{\mu} (\mu = 1,\cdots, M)$ を $M$ 個の観測値として, $M$ 次元ベクトルで表します.
y = w_{0} + \sum_{\mu=1}^{M} w_{~\mu}~x_{~\mu} +\epsilon
単回帰分析と同様に,
- $\epsilon$ を入れなければ 最小二乗法
- $\epsilon$ を入れるならば 最尤推定
を用いたパラメーターのフィッティングができ, 単回帰分析とほとんど同じような計算でモデル作成ができます.
注意
線形重回帰モデルでの注意は多重共線性です. これは説明変数の間に強い相関が存在していることです. 多重共線性が存在していると説明変数間の強い相関によってパラメーター$(w_{\mu})$を求めるのに十分な連立方程式が足りなくなってしまい, 解が一意に定まらなくなってしまいます.
$x_{0}=1$として次の節から和の計算を省略する記法を用います:
w_{0} + \sum_{\mu=1}^{M} w_{\mu}x_{\mu}
= \sum_{\mu=0}^{M} w_{\mu}x_{\mu}
= w_{\mu} x_{\mu} = \boldsymbol{w}\cdot\boldsymbol{x}
レベル4:線形回帰モデル(線形基底関数モデル)
レベルアップ:説明変数 $x$ を連続関数に代入して加工する
ここまでは複数の説明変数 $x_{\mu}$ と目的変数 $y$ の関係が線形になるように表現してきました.
しかし, 世の中の現象は複雑で, 例えば時刻 $t$ における物体の落下距離 $x$ は $x=t^2$ のような二次関数で表現されます.
ここではより表現力を持たせるために説明変数 $x_{\mu}$ の非線形な効果も考慮します.
線形重回帰モデルの $\boldsymbol{x}$ を非線形な関数に代入した次の拡張を考えてみましょう.
y = w_{\mu} \phi_{\mu}(\boldsymbol{x}) + \epsilon
= \boldsymbol{w} \cdot \boldsymbol{\phi}(\boldsymbol{x}) + \epsilon
記号について整理します
- $\boldsymbol{x}$ は説明変数で $M$ 次元ベクトル
- 関数 $\phi_{\mu}(\boldsymbol{x})$ は $L$ 次元ベクトルの第 $\mu$ 成分で一般に $\boldsymbol{x}$ の非線形関数で基底関数と呼ばれます
- $\phi$ は $\mathbb{R}^{M} \to \mathbb{R}^{L}$ に送る写像で $\phi_{\mu}(\boldsymbol{x})$ によって記述される空間を特徴量空間と呼ばれます
- $\boldsymbol{w} \cdot \boldsymbol{\phi}(\boldsymbol{x}) = \sum_{\mu=0}^{L} w_{\mu} \phi_{\mu}(\boldsymbol{x}) $
- $w_{\mu}$ はモデルのパラメータで, 特に $\phi_{0}(\boldsymbol{x}) = 1$ のとき $w_{0}$ はバイアスパラメータです
特徴量空間は説明変数として用意したパラメータをよりモデルの説明力を上げるために加工した説明変数の世界と考える事ができます.
注意
線形単回帰と線形重回帰モデルという呼び方はともにパラメータ$x_{\mu}$の一次関数でモデルを作成しているため線形と呼ばれていることに納得できます.
一方で線形回帰モデルは一般に$\phi$が非線形関数であるため線形モデルと呼べないように思えまが, この線形とはモデルパラメーター $w_{\mu}$ と目的変数 $y$ の関係が線形であることから線形回帰モデルと呼ばれています. 実際にモデルを作成するときは $x$ には観測値を入れるため $\boldsymbol{\phi}(\boldsymbol{x})$ には何かしらの値が入っていることを考えれば問題は線形代数で解けます.
(たまに線形基底関数モデルのことを非線形回帰モデルと呼ばれていたりしますが正しくないです. むしろ一般化線形回帰モデル(レベル5)が非線形回帰モデルの一部であるとみなすべきです. )
一般型とパラメータの推定
レベル4までは全て線形回帰モデルとして統一的な記述ができます:
- $ X_{n,\mu} = x_{n,\mu} $ ($N\times M$行列)
- $\Phi_{n,\nu}(X) = \phi_{\nu}(\boldsymbol{x}_{i})$ ($N\times (L+1)$行列)
- $\boldsymbol{w} = (w_{1},\cdots,w_{L})^{T}$ ($L+1$次元ベクトル)
- $\boldsymbol{y} = (y_{1},\cdots,y_{i})^{T}$ ($N$次元ベクトル)
- $\boldsymbol{\epsilon} =(\epsilon_{1},\cdots,\epsilon_{i})^{T}$ ($N$次元ベクトル)
とすると
\begin{align*}
\boldsymbol{y} &= \Phi(X) \boldsymbol{w} + \boldsymbol{\epsilon}\\
y_{i} &= \phi_{\nu}(\boldsymbol{x}_{i})w_{\nu} + \epsilon_{i}
\end{align*}
で記述することができ, 注意でも述べたように $\Phi_{n,\nu}(X)$ は何かしらの実数値が入っている行列で計画行列と呼ばれます.
ガウス分布に従う誤差を考えている場合 $\boldsymbol{w}$ についての方程式
\Phi(X)^{T} \Phi(X) \boldsymbol{w}= \Phi(X)^{T}\boldsymbol{y}
が得られ, これを正規方程式と呼びます. $\Phi(X)^{T} \Phi(X)$ が逆行列を持つとき一般解が得られ $\boldsymbol{w} = \left(\Phi(X)^{T} \Phi(X)\right)^{-1}\Phi(X)^{T}\boldsymbol{y}$ として得られます.
$\epsilon$ がガウス分布に従っている限り, 線形回帰モデルでも結局は $
y \sim \mathcal{N}(\boldsymbol{w} \cdot \boldsymbol{\phi}(\boldsymbol{x}), \sigma^{2})$ であるため, 最尤推定(もしくは最小二乗法)を用いて 線形重回帰と同様に一般解を厳密に求めることができます.
具体例:
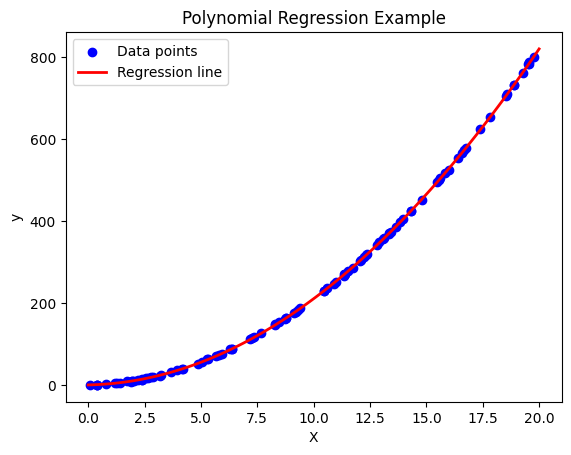
例1:多項式回帰
$M=1$とする. 基底関数 $\phi(x)_{\nu} = x^{\nu}$ という冪乗にすると,
y = w_{0} + w_{1}x + w_{2}x^{2} + w_{3}x^{3} + \cdots w_{L} x^{L} +\epsilon
= \sum_{\nu=0}^{L} w_{\nu} x^{\nu} +\epsilon
という多項式回帰モデルが得られます.
たとえば$x^2$までに従うモデルを作成してみると次のような回帰曲線が得られます.
例2:動径基底関数・ガウス基底関数
また別の例で, $M=1$として, 規格化されていないガウス分布を基底関数とするものも用いられる.
\phi_{j}(x) = e^{- \frac{(x-\mu_{j})^2}{2s^{2}}}
これはガウス分布をパラメータの重み付けで重ね合わせるモデルになります.
$\mu_{j}, s^2$ は事前に手で与えるパラメータです. この特徴量関数を用いたモデルは実はガウス過程回帰と関連しています.
レベル5:一般化線形回帰モデル(GLM)
レベルアップ: $y$ の従う分布を一般化し,パラメータ$w$との関係を非線形化する
ここまでのモデルはすべて $y$ と $w$ の間に単純な線形関係があり, $y$ の従う確率変数も連続値で考えやすいものだけでした. そのため モデルのパラメータに対して厳密な解を構築できました. ここでは更に一般化して, その線形性を無くし, より広い確率分布に従うように拡張することで, モデルの表現力を向上させます.
ここまでの線形回帰モデルでは $ \epsilon $ として連続値で値域には制限ではありませんでしたが, 一般化線形回帰モデルを考えることで $Y$ として例えば 0,1の二値の離散値しか取らないときにも適応できるモデルを考える事ができるようになります.
一般化線形回帰モデルは目的変数の平均値と説明変数を非線形関数でつなげるモデルです.
\begin{align}
\text{確率モデル}:\, & E[Y] = f\left(\sum_{\mu=0}^{L} w_{\mu} ~ \phi(\boldsymbol{x})_{\mu} \right)
\end{align}
このように表されるモデルを一般化線形回帰モデルと呼びます. 目的変数 $y$ の期待値とパラメータ $ w_{\mu}$ の間を非線形な関数 $f(a)$ で結びつけるのが特徴です.
ここで用語の整理です:
- 線形予測子もしくは活性:$ a := \boldsymbol{w} \cdot \phi(\boldsymbol{x})$
- 活性化関数:$f(a)$
- リンク関数:逆関数 $f^{-1}$
と呼ばれます.
ここで注意ですが, 活性化関数は自由には選べません. 確率変数 $Y$ の値域(正確には $E[Y]$ の値域)であったり, 活性の定義域なども考慮する必要があります.
一般化線形回帰の仮定
一般化線形回帰モデルでは観測データ $D = \lbrace(x_{i},y_{i})| i = 1,\cdots, N\rbrace $ として, 説明変数を活性化関数に入れた値を $z_{i} = f(a_{i}) = f( \boldsymbol{w} \cdot \phi(\boldsymbol{x_{i}}))$ とします.
一般化線形回帰の仮定は2つです:
- 確率変数 $Y$ は指数型分布族 $ p(y|\eta,s) = \frac{1}{s}h\left(\frac{y}{s}\right) g(\eta) \exp(\frac{\eta y}{s})$ に従う.
- $Y_{i}$の期待値に対して $E[Y_{i}] = z_{i} = f(a_{i})$ を仮定とします.
注意:指数型分布族はガウス分布を含む広いクラスの分布です
一番最後の仮定が重要で, 目的変数の確率変数 $Y$ の期待値が活性化関数を通じて説明変数 $x$ と結びついていることを表しています.
この仮定によって $y_{i} = f(a_{i}) + \epsilon $ のような単純な確率変数の足し算で得られるモデルを拡張しています. 例えば2値分類モデルなどが最も有名な具体例になります.
パラメータの最尤推定
指数型分布族の期待値と一般化線形回帰の仮定から $E[Y]= -s\frac{d}{d\eta} \ln{g(\eta)}=z$ であるため $z,\eta$ には関係があり, それを $\psi(z)=\eta$ としておきます.
パラメータ $w$ の最尤推定を行うために, 対数尤度の $\ln p(\boldsymbol{y}|\eta,s) = \sum_{n=1}^{N}\ln p(y_{i}|\eta,s) $ を $\boldsymbol{w}$ で微分してみましょう. $\eta_{i} =\psi(z_{i}) = \psi(f(a_{i})) = \psi(f(\boldsymbol{w} \cdot \phi(\boldsymbol{x_{i}}))) $ に注意して連鎖微分を行うと
\begin{align}
\nabla_{w}\ln p(\boldsymbol{y}|\eta,s)
&= \sum_{n=1}^{N} \nabla_{w}\left( \ln{g(\eta_{i})} + \frac{y_{i}}{s}\right)\\
&= \sum_{n=1}^{N} \left( \frac{d}{d\eta}\ln{g(\eta_{i})} + \frac{\eta_{i} y_{i}}{s}\right)\frac{d\eta_{i}}{dz_{i}}\frac{dz_{i}}{da_{i}}
\nabla_{w} a_{i}
\end{align}
となります. 計算するために,
- $-s\frac{d}{d\eta} \ln{g(\eta)}=z_{i}$ (一般化線形回帰の仮定)
- $\frac{d\eta_{i}}{dz_{i}} = \psi'(z_{i})$, $\frac{dz_{i}}{da_{i}} = f'(a_{i}) $
- 仮定として $f^{-1}(z) = \psi(z) = \eta = a$ つまり, $f(\psi(y))=y$ とします. これから $ \psi'(z)f'(a) = 1$ が得られます
これらを使うと対数尤度 $l$ の $\boldsymbol{w}$ の微分は
\begin{align}
- \nabla_{w} l
&= -\nabla_{w}\ln p(\boldsymbol{y}|\eta,s) =\frac{1}{s}\sum_{n=1}^{N} \left(y_{i}-z_{i} \right) \boldsymbol{\phi(x_{i})} \\
&= \frac{1}{s}\sum_{n=1}^{N} \left(y_{i}-f(\boldsymbol{w} \cdot \phi(\boldsymbol{x_{i}})) \right)\boldsymbol{\phi(x_{i})}
\end{align}
で得られます. これはよく見ると最小二乗法で目的関数をパラメータで微分したときの式に似ており, 例えば $f$ が恒等関数であるときにこれは最小二乗法と同じ式になります.
(※ただし $Y$ の従う分布がガウス分布とは限らないことに注意)
注意
$y$ と $w$ の関係が非線形になってしまうため線形回帰モデルのように厳密な解を求めるのは難しく, 何かしらの近似手法・近似アルゴリズムで求める必要があります. そこでよく使われるのがラプラス近似です. 一般の書籍だとラプラス近似についてページを割いている事が多いですが, これは飽くまでも近似的に解を求める方法を語っているだけでモデルの本質を語っているわけではないので切り分けて考えることが必要です.
具体例
例1:ロジスティック回帰
よくある例がロジスティック回帰で指数型分布族に対して,
- $s = 1$
- $h(t)= 1$
- $g(\eta) = \sigma(-\eta) = \frac{e^{-\eta}}{1+e^{-\eta}}$
- $\eta=a$
とすると
p(y|\eta) = \sigma(-\eta)\exp(t\eta)
= (1-\theta)\left(\frac{\theta}{1-\theta}\right)^{y}
= \theta^{y}(1-\theta)^{1-y}
が得られ, $y$は $0,1$の2値を取るベルヌーイ分布です. ただし $\eta = \ln(\frac{\theta}{1-\theta})$であり, $\sigma(a)$ はロジスティック関数です.
活性関数を $f(a) = \frac{1}{1+e^{-a}}$とすると
E[y] = \frac{1}{1+ e^{-\left(w\cdot \phi(\boldsymbol{x}) \right)}}
で表されるモデルつまり ロジスティック回帰が得られます. ロジスティック回帰では $y$ の観測値を $[0,1]$ の間に制限することができるため2値分類と相性がよいです. またこの場合は $z=f(a)$ は $y=1$ となる確率を表しています.
二値分類のロジスティック回帰だとこのような画像が得られると思います.

例2:プロビット回帰モデル
ロジスティック回帰モデルの確率分布の仮定は同じで活性化関数を別の関数に選んでみましょう.
$ f(a) $ として正規分布の累積分布関数とするとプロビットモデルになります. 名称の由来は 正規分布の累積分布関数の逆関数がプロビット関数と呼ばれるためです.
プロビット回帰モデルは $Y$ の従う確率分布は同じですが, 活性化関数が異なっているという違いがあります. 一般に確率変数の値域をみて活性化関数を選ぶ必要があります.
例3:線形回帰モデル
ちなみに$Y$の従う分布をガウス分布として, 活性関数$f(a)$を恒等関数つまり,
E[t] = f(a) = a = w\cdot \phi(\boldsymbol{x})
としたとき線形回帰モデルが得られ, 一般化であるとわかります.
注意
一般化線形回帰には等分散性が存在しません.
レベル6: 最大事後確率推定(MAP推定)
レベルアップ:モデルのパラメーター$w$を確率変数に格上げする
ここまでは $y$ のみが観測誤差のために確率変数として扱われていました. またこれまでの回帰モデルでは全て「事象を説明する真のモデルがただ一つ存在している」という仮定のもとで行われてきました.
さらに $w$ を確率変数に格上げすることで, 「モデルのパラメータもその時その時で変わるもの」だという仮定を行うのが今回のレベルアップ内容です. このレベルアップによりモデルの パラメータ$w$を確率変数に格上げする ことで
- 正則化を行うことができたり
- パラメータについての自身の仮説を反映させたり
- 次のベイズ回帰モデルへの準備ができる
ようになります.
ここまでのモデルは $y$ が確率変数であり, $x,w$ はパラメーター(確定値)であったため, $p(y|x,w)$ で表すことができました. これは $x,w$ を決めたという条件のもとで $y$ の値が出力される確率, つまり条件付き確率であるということを表していました.
事前分布と事後分布
今回のレベルアップではこのパラメータ $w$ は何かしらの確率分布 $p(w)$ に従っていると仮定することでとにかく確率変数であると仮定します.
条件付き確率の定義から
p(y|x,w) p(w) = p(y,w|x)
を通じて $w$ と $y$ の同時確率分布を考える事ができる様になります.
$p(w)$ は事前分布と呼ばれ, この選び方はモデルパラメータに関する何かしらの知見が反映されます. よく用いられるのはガウス分布です. また, 事前分布としてガウス分布を用いたときにその分散を無限大にすることで全くなんの知見もないという仮定を入れていると解釈することも可能で, これを無情報事前分布と呼びます. 事前分布を一意に定める数学的な取り決めは存在しないため客観的でないことから $w$ は主観確率と呼ばれます.
回帰分析では観測データからモデルのパラメータ $w$ を求める必要があります. モデルのパラメータ $w$ を確率変数に持ち上げたときどのようにパラメータを推定すればよいでしょう?
少し復習です. 最尤推定では
L = \prod_{i=1}^{N} p(y_{i}|x_{i},w)
が観測した説明変数と目的変数 $(x,y)$ のデータが得られる尤もらしいパラメータとして $L$ が最大になるような $w$ が得られるのでした.
これは目的変数 $y$ だけが確率変数であったのでこのような処置をしていたのです. しかし, 今は $w$ も確率変数であるためベイズの定理
P(A,B)=P(B|A)P(A) = P(A|B)P(B)
を利用して, 尤度関数ではなく,
p(w|D) = \frac{p(w)\prod_{i=1}^{N} p(y_{i}|x_{i},w)}{\prod_{i=1}^{N}p(y_{i})}
\propto p(w) \prod_{i=1}^{N} p(y_{i}|x_{i},w) = p(w)L
が最大になるような $w$ 直接計算することができます. ここで, $p(w|D)$ を $w$ についての事後分布と呼びます.
事後分布は事前分布と観測データ $D$が得られたときに尤もらしいパラメータ $w$ が得られる確率そのものです.
事後分布の計算
事後分布を計算するための準備:
- 事前分布: $w$を出力する確率分布 $p(w)$を導入する.
- 目的変数 $y$ を説明する確率モデル $p(y|x,w)$ の仮定
- 観測データ: $ D = (\boldsymbol{x},y)_{i} , (i= 1,\cdots,N )$
- 尤度関数: $L=p(D|W)= \prod_{i=1}^{N} p(y_{i}|x_{i},w) $
以上の準備のもとで事後分布
p(w|D) = \frac{p(w) L}{p(y)} = \frac{p(w)\prod_{i=1}^{N}p(y_{i}|x_{i},w)}{p(y)}
で与えられ, 最大事後確率推定はそのままの通り事前分布が最大となる点 $w^{*}$ によってモデルパラメータを推定することになります.
ただし, $p(y) = \int dw p(D|W)p(w) $で周辺分布と呼ばれますが最大事後確率推定においては無視して問題ないです.
この事後分布を最大化するには$p(w|D)$を$w$で偏微分すれば良いですが, 分母の $p(y)$ は $w$ に依存していないため無視できます. 計算しやすいのは対数事後分布 $-\log p(w)$ で極値の計算をすると
-\frac{\partial}{\partial w}\log p(w|D) = -\frac{\partial}{\partial w} l -\frac{\partial}{\partial w} \log p(w)
ですが, 例えば $p(w) = \mathcal{N}(0,\sigma)$ としてガウス分布を選んでおくと
-\frac{\partial}{\partial w} \log p(w) = \frac{1}{ \sigma^{2}} w
となり, $\lambda = \frac{1}{\sigma^{2}}$ とするとこれは最尤推定に正則化項を付け足した形になっています.
モデルパラメータの事後分布が最大になる $w^{*}$
w^{*} = \text{argmax}_{w}\log p(w|D)
をMAP推定解と呼びます. このモデルは正規化項を導入した一般化線形回帰モデルとしても考えることができ, 過学習を極力避ける事ができるモデルとして解釈ができます.
(注意)
MAP推定で行ったのはモデルのパラメータを点推定しただけであり, ベイズ的なモデルとは言えないです. まれにMAP推定を指してベイズ回帰モデルという記述を見ますがそれは誤りです.
レベル7-A: ベイズ回帰モデル
レベルアップ:モデルのパラメーターの事後分布で重みづけて $y$ のモデルを推定
最大事後確率推定(MAP推定)では
- モデルパラメータ $w$ に事前分布を導入して確率変数に格上げ
- 観測値から $w$ の事後分布を推定
- 事後分布が最大となるパラメータ $w$ を点推定
として予測分布 $p(y^{*}|x^{*},D)$ を作成しました. 最大事後確率推定では, 事前分布をガウス分布とすると正規化を行っており過学習をできる限り回避する事ができるモデルとして解釈できるのでした.
ベイズ回帰モデルでは, モデルのパラメータを点で推定するのではなく分布そのもの(事後分布)を推定し, その事後分布に対して仮定しているモデルを平均化することですることで, 一点ではなくパラメータの広がりを表す分布の情報をまんべんなく拾ってくることで予測に活かすことを目指します.
例えば、
のような事後分布が得られているとします。このような多峰な分布であるとMAP推定では一つの峰しか選択されませんが、ベイズ推定では別の峰のパラメータも考慮したモデルが作成されます。
そのため $p(w|D)$の事後分布そのものを求めることが重要になりますが, 一般の場合において解析的に求めることは難しいです. これらを計算アルゴリズムで求める方法の一つがMCMC(マルコフチェーンモンテカルロ)などになります. 多くの教科書ではMCMCなどの説明に多くのページを割いていますが, ここでは割愛して回帰モデルとしてどのようにMAP推定と異なっているのかを議論します.
ベイズ回帰モデル
MAP推定では事後分布が最大になる $w$ を求めることが最終目的でしたが, ベイズ回帰モデルは $w$ を生成する $p(w|D)$ そのものを求めることが目的に変わりました.
そして回帰モデルでは説明変数$x$の値から目的変数$y$を求めることでした. モデルパラメータ$w$の事後分布を求めた後に, 新しい次に予測したい説明変数$x^{*}$に対して$y^{*}$を推定する確率モデルとして
p(y^{*}|x^{*},D)= \int dw ~ p(y^{*}|x^{*},w)p(w|D)
で与えられるのが予測分布となります. この予測分布の記法はこれまで観測してきたデータ $D$ と予測したい観測データの説明変数をもとに $y^{*}$ の予測分布を求める事ができました.
しかしこのままでは回帰モデルとしては不十分で, $y^{*}$ の予測分布はわかりましたが $y^{*}$ の予測値を決定できていません. そこでよく用いられるのは平均値で,
y^{*} = f(x^{*}) = E[y^{*}] = \int dy^{*} ~ y^{*} ~ p(y^{*}|x^{*},D)
とすることで回帰モデルとして完成しました.
補足
ベイズ回帰モデルのメリットは次のようなものが挙げられます
- 一般にパラメータの点推定を行っているわけではないので過学習を回避しやすくなります.
- 観測したデータから得られる予測分布において, 分散を評価することによって精度が不安定なデータ点が明示的になる. このような点の学習データを得ることでよりモデルの精度向上につながります. これを能動学習と呼びます.
レベル7-B: 深層学習モデル
レベルアップ:特徴量空間への射影を複数回行う
一般化線形回帰モデルでは説明変数とモデルパラメータの線形結合(線形予測子$ a = w\cdot \phi(\boldsymbol{x})$)を非線形関数に代入することで目的変数を回帰していました
y = f(a) = f( w\cdot \phi(\boldsymbol{x}))
深層学習では活性化関数に代入することを多段階で行うことにより複雑なモデルを作成できるモデルです.
$\boldsymbol{x} \in \mathbb{R}^{H^{(0)}} $ から2層を経て $L$次元のベクトル $\boldsymbol{y} \in \mathbb{R}^{L}$を予測するモデルを考える.
\begin{align}
a_{j}^{(1)} &= \left(W^{(1)} \cdot \boldsymbol{x}\right) =
\sum_{i=1}^{H^{(0)}}w_{ji}^{(1)}x_{i} \,, \quad \boldsymbol{a}^{(1)}\in \mathbb{R}^{H^{(1)}}\\
z_{j}^{(1)} &= \phi^{(1)}\left(a_{j}^{(1)}\right)\,, \quad \boldsymbol{z}^{(1)}\in \mathbb{R}^{H^{(1)}}\\
a_{j}^{(2)} &= \left(W^{(2)} \cdot \boldsymbol{z}^{(0)}\right) =
\sum_{i=1}^{H^{(1)}}w_{ji}^{(2)}z_{j}^{(1)} \,, \quad \boldsymbol{a}^{(2)}\in \mathbb{R}^{H^{(2)}}\\
z_{j}^{(2)} &= \phi^{(2)}\left(a_{j}^{(2)}\right)\,, \quad \boldsymbol{z}^{(2)}\in \mathbb{R}^{H^{(2)}}\\
y_{j} &= z_{j}^{(2)}+\epsilon_{j} \,
\end{align}
各変数の肩の添字$(1),(2)$は階層を表しています.
深層学習での用語をまとめます:
- 活性: $a_{j}^{(1)},a_{j}^{(2)}$
- 活性関数のベクトルの次元 : $H^{(1)},H^{(2)}$
- 隠れユニット : $z_{j}^{(1)},z_{j}^{(2)}$
- 活性化関数 : $\phi^{(1)},\phi^{(2)}$
と呼びます.
活性化関数は必ず非線形関数です. もし線形関数ならば線形回帰モデルと等価なモデルとなります. これは恒等写像を含める線形写像の場合は $x$ から $y$ までのパラメータの関係が適切な置き換えのもとで線形写像として表現できるからです. 活性化関数としては, シグモイド関数, $\tanh$ 関数や標準正規分布の累積分布関数などが用いられる事が多いです.
ここで一つ注意をしておきます. 上記の表式を見ると階層を一つだけに絞り $y_{j} = z_{j}^{(1)} +\epsilon_{j}$ とすると,
- $\boldsymbol{a}^{(1)} = \sum_{i=1}^{H^{(0)}}w_{ji}^{(1)}\phi(\boldsymbol{x})_{i}$ をリンク関数
- $y_{i} = z_{i}^{(1)} + \epsilon_{j}= f(a_{i}^{(1)})+\epsilon_{i}$
で考えると, 確率変数 $y$ をガウス分布に従うと仮定したときの, 一般化線形回帰と等価であることがわかります. この意味で深層学習もまた一般化線形回帰モデルを拡張しただけであると考えることができます.
深層学習ではパラメータと目的変数の間の関係を非線形関数にして, 更に層化させることで表現力を高めているモデルになります.
より$L$段階の階層を考えて一般に第$l$層目の隠れユニットと活性を
\begin{align}
a_{j}^{(l)} &= \sum_{i=1}^{H^{(l-1)}}w_{ji}^{(l)}z_{j}^{(l-1)} \,,\\
z_{j}^{(l)} &= \phi^{(l)}\left(a_{j}^{(l)}\right) \,,\\
\end{align}
で定義して
y_{j} = z_{j}^{(L)}+\epsilon_{j}
とすればよいです.
モデルを決定するためには最小二乗法でもよいし, $\epsilon$を 一般の確率変数であると仮定して最尤推定を用いても良いです.
- 最小二乗法: $E = \sum_{n=1}^{N}\left(\boldsymbol{y} - \boldsymbol{z}^{(L)}\right)^2$ を$w^{(l)}_{ij}$について最小化する
- 平均が$\mu =y_{j} = z_{j}^{(L)}$となるような $\epsilon$ の分布 $p(\boldsymbol{y}|\boldsymbol{x}, w_{ij}^{(l)})$ に対して対数尤度
$l = \sum_{n=1}^{N}p(\boldsymbol{y}|\boldsymbol{x},w_{ij}^{(l)})$ を最大化する
特に $\epsilon$ がガウス分布に従っているときは最尤推定と最小二乗法の結果は一致します.
回帰モデルとしてはレベル5一般化線形回帰でも議論したように, $y_{j} = z_{j}^{(L)}$ とするか, $E[y] = y_{j} = z_{j}^{(L)}$ とすれば良いです.
レベル8: 深層ベイズモデル
レベルアップ:ベイズモデルと深層学習を組み合わせる
ここまでのレベルアップのダイジェストにまとめると
- 説明変数 $x$ を多次元に拡張し, 非線形関数に代入して$\Phi(X)$ として扱った
- 目的変数 $y$ を確率変数として取り扱った
- $E[Y] = f(X)$ のように目的変数の期待値と説明変数の間を非線形関数で繋ぐことでより一般の確率変数として扱った
- モデルパラメータ $w$ も事前分布によって確率変数として扱った
- 観測データ $D$ をもとにモデルパラメータ $w$ の従う分布(事後分布)を推定して, 回帰に応用してきた.
- 活性化関数を多段階化することで深化し表現力を向上させた
です. これらを全てまとめたものが深層ベイズモデルになります.
深層ベイズモデルのセットアップを行います
- $W$ を全ての階層のパラメータ $w_{ij}^{(l)}$ をまとめたパラメータとします
- $\boldsymbol{y} = f(X)$ の $f(\cdot)$ として深層学習モデルを利用します. つまり, 以下のようにします
\begin{align*}
\boldsymbol{y} = f(X)
&= \phi^{(L)}(\boldsymbol{w}^{(L)}\cdot\phi^{(L-1)}(\cdots (\boldsymbol{w}^{(2)}\cdot\phi^{1}(\boldsymbol{w}^{(1)}\cdot\boldsymbol{x})))) \\
&= \phi^{(L)}\circ (\boldsymbol{w}^{(L)}\cdot\phi^{(L-1)}) \circ \cdots \circ( \boldsymbol{w}^{(2)}\cdot\phi^{(1)})(\boldsymbol{w}^{(1)}\cdot\boldsymbol{x})
\end{align*}
- $y$の従う確率分布は $y \sim \mathcal{N}(f(Z),\sigma)$ という平均が深層学習であるとする
- 全てのパラメータ $w_{ij}^{(l)}$ の従う分布(事前分布)はガウス分布である
とします.
すると レベル7-A で議論したのと全く同様に モデルパラメータ$W$の事後分布を求めた後に, 新しい次に予測したい説明変数$x^{*}$に対して
p(y^{*}|x^{*},D)= \int dw ~ p(y^{*}|x^{*},w)p(w|D)
で与えられるのが予測分布となります. 回帰モデルも同様に
y^{*} = f(x^{*}) = E[y^{*}] = \int dy^{*} ~ y^{*} ~ p(y^{*}|x^{*},D)
で与えられます.
結局$y,x$の予測分布をガウス分布として, その平均に深層学習$f(X)$
となるように調整するだけでベイズ回帰モデルと同様のロジックでモデルの作成が可能となります.
更にここでは確率モデルとしてガウス分布に従うと仮定しましたが, 一般化線形回帰の仮定と同様に
E[Y] = f(X)
として 一般化線形回帰+深層学習+ベイズ回帰モデルを作成することができます.
メリット
過学習を抑える
一般に深層学習ではその高い表現力から十分なデータが無い限り過学習におちいってしまします.そこで、正則化やドロップアウト法などによって過学習を抑える方法が様々に考えられます.
ベイズ回帰モデルの過学習を抑える性質を用いて, パラメータの点推定ではなくパラメータの事後分布をもとにした重み付けをからモデルの予測分布を作成できます.
能動学習
画像認識の世界では大量の学習データが必要でネット上には大量の画像が存在しますが、それぞれなんのラベルも与えられておらず、学習データとするためには人の手でラベル付与を行う必要があります. しかし人の手が必要なので効率的にラベル付きのデータを準備する必要があります.
不確実性を考慮するモデルでは予測の不確実性が大きくなるようなものを選択してラベルを付与することで効率的に学習データを準備できるようになります.
このようにモデルの予測の不確実性が大きくなる点のデータをモデル自身に申告させることを能動学習と呼びます.
まとめ
以上のようにこれら全てのモデルは解釈次第では一本道で理解できる事がわかりました.
今回は計算アルゴリズムや高速化手法、メリット・デメリットについては触れる事ができませんでしたが参考文献などにそういった内容がまとまっているので興味がある方はぜひ本を取って見ると良いと思います.