UMAP: 次元削減アルゴリズム

uMap

Last updated at 2024-08-15Posted at 2024-08-15

UMAP（Uniform Manifold Approximation and Projection）は、データの次元削減と可視化のための強力なアルゴリズムです。t-SNEと同様にデータの可視化に使用できますが、一般的な非線形次元削減にも適用可能です。UMAPは以下の3つの仮定に基づいています：

データはリーマン多様体上に一様に分布している
リーマン計量は局所的に一定（または近似的に一定）である
多様体は局所的に連結している

リーマン多様体（リーマン・マニフォールド）について

UMAPは元のデータの構造を「ファジー・トポロジー」として捉えます。これは、データ点間の関係を厳密な二値（つながっている/つながっていない）ではなく、連続的な度合いで表現するものです。この表現により、データの微妙な構造や関係性を柔軟に捉えることができます。次に、UMAPはこのファジー・トポロジー構造を可能な限り保持しながら、データを低次元空間に射影します。つまり、元のデータの複雑な関係性を、より単純な空間でも再現しようと試みるのです。この過程で、UMAPは局所的な構造と大域的な構造の両方を考慮します。局所的な構造とは近くのデータ点同士の関係を指し、大域的な構造はデータ全体の分布や傾向を指します。結果として、UMAPは高次元データの重要な特徴を保持しつつ、人間が理解しやすい2次元や3次元の表現を生成します。これにより、複雑なデータセットの視覚化や分析が容易になります。

UMAPの特徴：

高速な処理：大規模なデータセットでも効率的に動作します
局所構造と大域構造の保持：データの局所的な関係性と全体的な構造を同時に維持します
理論的裏付け：数学的に堅牢な基礎を持っています
柔軟性：さまざまなデータタイプや距離メトリックに適用可能です
スケーラビリティ：近似最近傍探索アルゴリズムを利用し、数百万のデータポイントまでスケールできます

UMAPは、以下のようなさまざまな用途に活用できます：

高次元データの可視化
特徴量エンジニアリング
クラスタリングの前処理
異常検知
時系列データの分析

Python: umap-learn

Pythonでは、umap-learnライブラリを使用してUMAPを簡単に実装できます。インストールは以下のコマンドで行えます：

pip install umap-learn

UMAPの基本的な使用方法は以下の通りです：

2次元版

import numpy as np
import matplotlib.pyplot as plt
import umap
from sklearn.datasets import load_digits

# データ(手書き文字データセット)の読み込み
digits = load_digits()
data = digits.data
target = digits.target

# UMAPの適用
fit = umap.UMAP(random_state=42)
u = fit.fit_transform(data)

# プロットの作成
plt.figure(figsize=(12, 8))

# 各数字ごとに異なる色でプロット
scatter = plt.scatter(u[:, 0], u[:, 1], c=target, cmap='tab10', s=5)

# 凡例の作成
legend_elements = [plt.Line2D([0], [0], marker='o', color='w', label=str(i), 
                   markerfacecolor=plt.cm.tab10(i/10), markersize=10)
                   for i in range(10)]
plt.legend(handles=legend_elements, title="Digits", loc="center left", bbox_to_anchor=(1, 0.5))

plt.title('UMAP embedding of the Digits dataset')
plt.xlabel('UMAP1')
plt.ylabel('UMAP2')

# レイアウトの調整
plt.tight_layout()
plt.show()

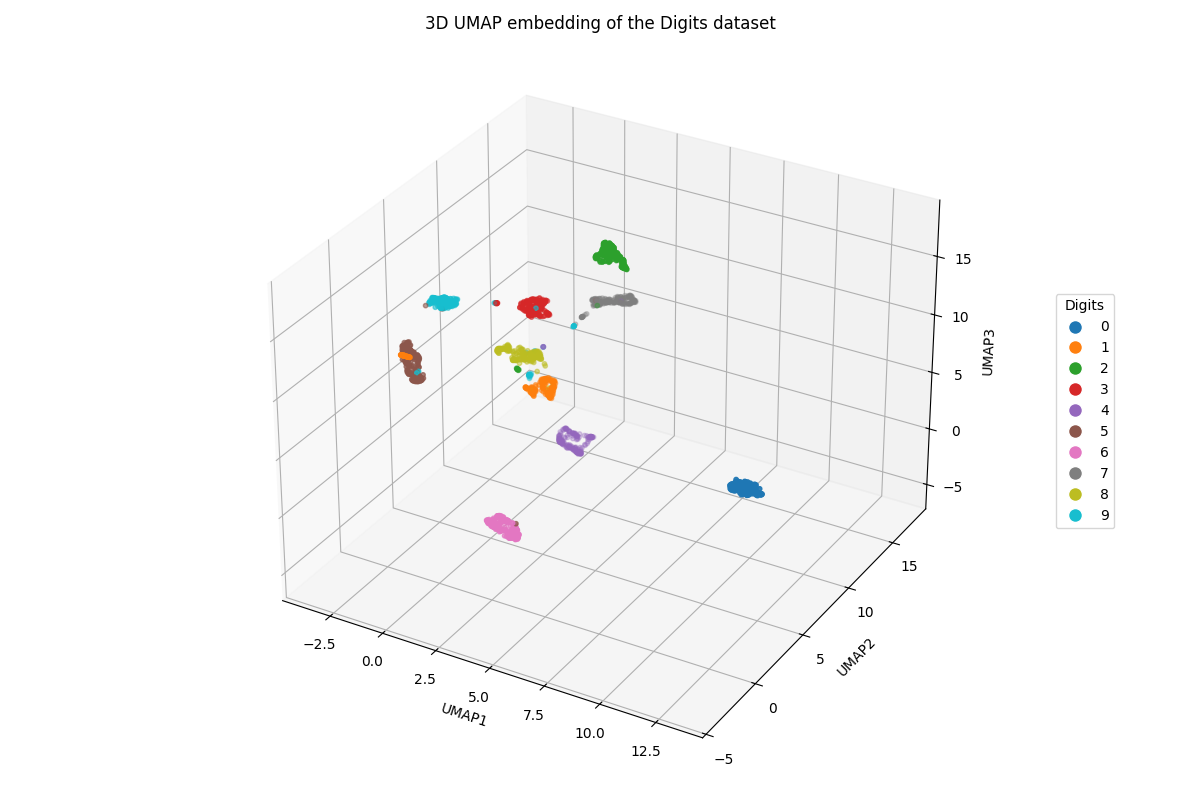
3次元版

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import umap
from sklearn.datasets import load_digits

# データの読み込み
digits = load_digits()
data = digits.data
target = digits.target

# 3次元UMAPの適用
fit = umap.UMAP(n_components=3, random_state=42)
u = fit.fit_transform(data)

# 3Dプロットの作成
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 各数字ごとに異なる色でプロット
scatter = ax.scatter(u[:, 0], u[:, 1], u[:, 2], c=target, cmap='tab10', s=10)

# 凡例の作成
legend_elements = [plt.Line2D([0], [0], marker='o', color='w', label=str(i), 
                   markerfacecolor=plt.cm.tab10(i/10), markersize=10)
                   for i in range(10)]
ax.legend(handles=legend_elements, title="Digits", loc="center left", bbox_to_anchor=(1.1, 0.5))

ax.set_title('3D UMAP embedding of the Digits dataset')
ax.set_xlabel('UMAP1')
ax.set_ylabel('UMAP2')
ax.set_zlabel('UMAP3')

# レイアウトの調整
plt.tight_layout()
plt.show()

UMAPクラスには、以下のような重要なパラメータがあります：

n_neighbors: 局所的な多様体構造の近似に使用される近傍点の数を決定します。大きな値を設定すると、より大域的な構造が保持されますが、詳細な局所構造が失われる可能性があります。一般的に5から50の範囲で設定し、10から15が適切な値とされます。
min_dist: 埋め込み時に点がどれだけ密集できるかを制御します。大きな値を設定すると埋め込まれた点がより均等に分布し、小さな値を設定すると局所構造に関してより正確に最適化できます。0.001から0.5の範囲が適切で、0.1が妥当な値とされます。
n_components: 出力の次元数を指定します。デフォルトは2で、2次元の可視化に適していますが、必要に応じて3次元以上に設定することも可能です。
metric: 入力空間での距離測定に使用するメトリックを決定します。多様なメトリックが既にコード化されており、numbaによってJIT（Just-In-Time）コンパイルすれば、ユーザー定義の関数も渡すことができます。

これらのパラメータを調整することで、データの特性に応じた最適な次元削減を行うことができます。例えば、n_neighborsを大きくすると大域的な構造がより保持され、min_distを小さくすると局所的な構造がより強調されます。

UMAPは、データサイエンスや機械学習の分野で強力なツールとして注目されており、複雑なデータセットの解析や可視化に大きな貢献をしています。

Javascript: umap-js

JavaScriptでもUMAPを利用できます。umap-jsというnpmパッケージが公開されており、ブラウザ上でUMAPを実行することが可能になりました。これにより、Webアプリケーションやインタラクティブな可視化ツールにUMAPを組み込むことができます。

umap-jsの基本的な使用方法は以下の通りです：

import { UMAP } from 'umap-js';

const umap = new UMAP();
const embedding = umap.fit(data);

umap-jsは非同期処理にも対応しており、大規模なデータセットを処理する際に進捗状況を確認することができます：

import { UMAP } from 'umap-js';

const umap = new UMAP();
const embedding = await umap.fitAsync(data, epochNumber => {
  // 進捗状況の確認やユーザーへのフィードバック
});

また、umap-jsでは教師あり投影やデータの変換など、Pythonのumap-learnと同様の機能が提供されています。これにより、JavaScriptを使用する開発者も高度な次元削減と可視化の手法を利用できるようになりました。

R: umap

R言語でも利用可能です。CRANで公開されているumapパッケージを通じて、RユーザーもUMAPの機能を活用できるようになりました。このパッケージは、McInnesとHealyによって2018年に発表されたUMAPアルゴリズムの2つの実装を提供しています：

スクラッチから書かれた実装：最近傍探索と埋め込みのためのコンポーネントを含みます。
Pythonの'umap-learn'パッケージのラッパー：別途インストールが必要です（詳細はパッケージのvignetteを参照）。

Rでの基本的な使用方法は以下の通りです：

library(umap)

# データの準備
data <- # your high-dimensional data

# UMAPの実行
umap_result <- umap(data)

umap-learnと同様のパラメータを設定できます：

n_neighbors: 近傍点の数
n_components: 出力の次元数
metric: 距離メトリック
min_dist: 埋め込み時の最小距離

クラスタリングへの応用

UMAPは、クラスタリングの前処理ステップとしても効果的に使用できます。密度ベースのクラスタリングアルゴリズムの性能を向上させるのに役立ちます。ただし、UMAPはt-SNEと同様に、密度を完全に保持するわけではないため、注意が必要です。

クラスタリングにUMAPを使用する際は、以下の点に注意してください：

UMAPは密度を完全に保持しないため、結果の解釈には慎重になる必要があります。
クラスタ内の偽の「裂け目」を作成する可能性があります。
得られたクラスタの妥当性を評価することが重要です。

派生: densMAP

densMAPアルゴリズムは、データのトポロジー構造に加えて局所密度情報も保持するようにUMAPを拡張したものです。この手法は、生物学の分野で、単一細胞の転写変動の評価に有用との報告があります。

まとめ

UMAPは、その理論的基礎と実用的な性能により、データ分析や機械学習の分野で重要なツールとなっています。Python、JavaScript、Rなど、複数のプログラミング言語でサポートされていることで、より多くの研究者や開発者がUMAPを活用できるようになりました。

UMAPは、高次元データの可視化や分析において強力なツールであり、その応用範囲は機械学習、生物情報学、金融分析など多岐にわたります。今後も、UMAPの理論的な発展や新しい応用分野の開拓が期待されます。

参考文献

UMAP: Uniform Manifold Approximation and Projection - GeeksforGeeks (アクセス日: 2024-08-15)
UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction — umap 0.5 documentation
McInnes, L, Healy, J, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, ArXiv e-prints 1802.03426, 2018
UMAP GitHub repository
umap-learn · PyPI (アクセス日: 2024-08-15)
umap-js - npm (アクセス日: 2024-08-15)
Narayan, A, Berger, B, Cho, H, Assessing Single-Cell Transcriptomic Variability through Density-Preserving Data Visualization, Nature Biotechnology, 2021
CRAN - Package umap (アクセス日: 2024-08-15)
Basic UMAP Parameters — umap 0.5 documentation (アクセス日: 2024-08-15)

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up