1. はじめに
沢山の実験データを一括でフィッティング処理することを目的に書きました。ひとつひとつデータを開いて、フィッティングして、結果のパラメータを記録して、とやっていると面倒くさいので…。ローレンチアンを例に進めますが、ファイルリストの作成→フィッティングという流れ自体は他にも応用が効くんじゃないかと思います。
2. 簡単にローレンチアンの話(飛ばしてOK)
ローレンチアン(ローレンツ関数)はこんな関数です。
$$ f(x) = A\frac{d^2}{(x - x_0)^2 + d^2}$$
グラフを描くと $x=x_0$ で極値 $A$ を取る山になります。$d$ は山の半値半幅(HWHM)です。なので半値全幅(FWHM)は $2d$ になります。電磁波の共鳴吸収曲線が丁度この形で書けるため、物理・工学の分野でよくでてきます。
3. サンプルデータ
実際にデータをいじった方がわかりやすいと思うので、サンプルデータを作ります。
import numpy as np
# パラメータの定義
intensity = 50 #強度
HWHM = 5 #半値半幅
a = 10 #データのばらつきの大きさ
# データファイルの作成
for X0 in range (-30, 31, 10):
filename = 'X0=' + str(X0) + '.dat'
with open(filename, 'w') as file:
file.writelines('X' + '\t' + 'Y' +'\n')
for X in range (-100,101):
Y = intensity * HWHM**2 / ((X-X0)**2 + HWHM**2) + a * np.random.rand() - 5
file.writelines(str(X) + '\t' + str(Y) + '\n')
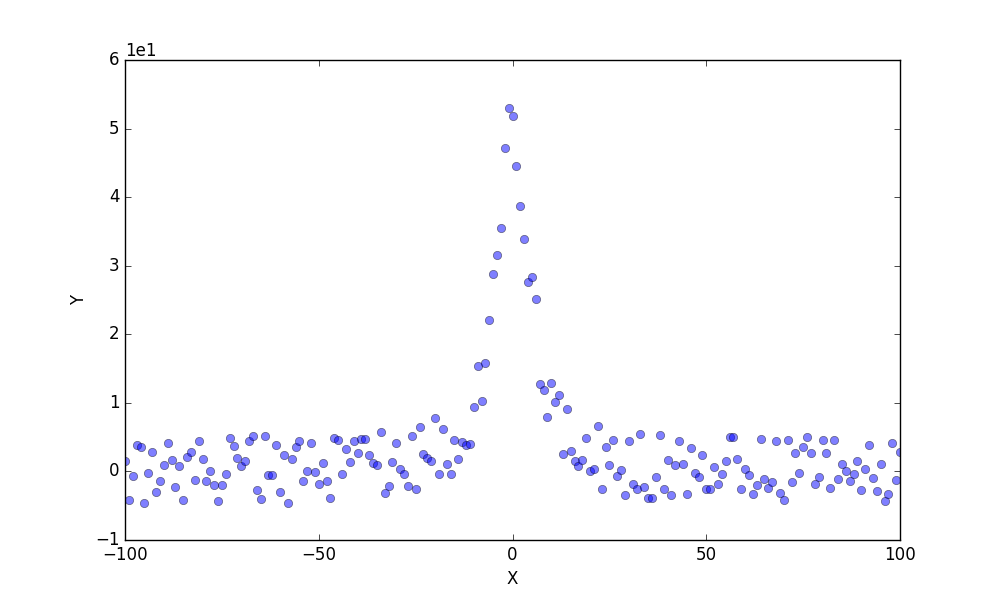
実行するとディレクトリ内に X0=-30〜30 まで、10区切りで7つのdatファイルができます。それぞれタブ区切りで (X, Y) 2列の数値データです。一行目にはインデックスとして X, Y (文字列)を書き込んでいます。中身はさっきのローレンツ関数で、Y=$f($X$)$ です。Yには乱数で若干ばらつきを与えています。例として「X0=0.dat」をプロットすると下のような感じです。
これからこの7つのdatファイルを一括でローレンチアンフィッティングして、各結果のグラフと、収束したパラメータを一つにまとめたdatファイルを作成したいと思います。
4. 一括でローレンチアンフィッティング
以下本題になります。作成した7つのdatファイルを一括でフィッティングして結果だけ貰いましょう。手順が追いやすいようにjupyterを使いたいと思います。ここからの大まかな流れを先に書いておくと、
- フィッティングするファイルのリストを作成
- イテレーションでリスト内のファイルを逐一フィッティング
- グラフを描画、収束したフィッティングパラメーターを別ファイルに書き出す
になります。
4.1 フィッティングするファイルのリストを作成する
イテレータで処理するために、globモジュールを用いて、これからフィッティングするファイルのリストfilelistを作成します。ここではワイルドカード*を使ってフォルダ中のX0=○○.datという名前のファイルだけリスト化します。ということで、jupyterでやりますが、
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ptick
import scipy.optimize
import glob, re
from functools import cmp_to_key
filelist = glob.glob('X0=*.dat')
filelist2 = []
for filename in filelist:
match = re.match('X0=(.*).dat', filename)
tuple = (match.group(1), filename)
filelist2.append(tuple)
def cmp(a, b):
if a == b: return 0
return -1 if a < b else 1
def cmptuple(a, b):
return cmp(float(a[0]), float(b[0]))
filelist = [filename[1] for filename in sorted(filelist2, key=cmp_to_key(cmptuple))]
filelist
['X0=-30.dat',
'X0=-20.dat',
'X0=-10.dat',
'X0=0.dat',
'X0=10.dat',
'X0=20.dat',
'X0=30.dat']
参考:Python: ファイル名の番号でソートする(外部サイト)
を実行します。In[2]でやっているのはリストの作成とリスト内のファイルソートです。globで捕まえるだけだと、文字列で並び替えられるため、数字の小さい順に並びません。それで大して困ることもないのですが、後々気持ち悪さも残るので、ここで数字の小さい順に並び替えています。
4.2 初期パラメータの推定とフィッティング
どうしてもループの中が少し長くなってしまうのですが…、こんな感じです。(後ろで説明します。)
result = open('fitting_result.dat', 'w')
result.writelines("filename\tA\tA_err\tX0\tX0_err\tHWHM\tHWHM_err\n")
for filename in filelist:
print(filename)
match = re.match('(.*).dat', filename)
name = match.group(1)
with open(filename, 'r') as file:
X, Y = [], []
for line in file.readlines()[1:]:
items = line[:-1].split('\t')
X.append(float(items[0]))
Y.append(float(items[1]))
# 初期値の推定(強度と中心値)
max_Y = max(Y)
min_Y = min(Y)
if np.abs(max_Y) >= np.abs(min_Y):
intensity = max_Y
X0 = X[Y.index(max_Y)]
else:
intensity = min_Y
X0 = X[Y.index(min_Y)]
# 初期値の設定
pini = np.array([intensity, X0, 1])
# フィッティング
def func(x, intensity, X0, HWHM):
return intensity * HWHM**2 / ((x-X0)**2 + HWHM**2)
popt, pcov = scipy.optimize.curve_fit(func, X, Y, p0=pini)
perr = np.sqrt(np.diag(pcov))
# 結果の表示
print("initial parameter\toptimized parameter")
for i, v in enumerate(pini):
print(str(v)+ '\t' + str(popt[i]) + ' ± ' + str(perr[i]))
# datファイルへのフィッティング結果の書き込み
result.writelines(name + '\t' + '\t'.join([str(p) + '\t' + str(e) for p, e in zip(popt, perr)]) + '\n')
# フィッティング曲線描画用の配列を作成
fitline = func(X, popt[0], popt[1], popt[2])
# 結果のプロットと画像の保存
plt.clf()
plt.figure(figsize=(10,6))
plt.plot(X, Y, 'o', alpha=0.5)
plt.plot(X, fitline, 'r-', linewidth=2)
plt.xlabel('X')
plt.ylabel('Y')
plt.ticklabel_format(style='sci',axis='y',scilimits=(0,0))
plt.savefig(name + ".png")
plt.close()
result.close()
X0=-30.dat
initial parameter optimized parameter
52.8746388447 52.1363835425 ± 1.37692592137
-29.0 -30.2263312447 ± 0.132482308868
1.0 5.01691953143 ± 0.187432386079
・・・
(中略)
・・・
X0=30.dat
initial parameter optimized parameter
50.0825336071 50.5713312616 ± 1.54634448135
31.0 30.1170389209 ± 0.149532401478
1.0 4.89078858649 ± 0.211548017933
ひとつひとつ説明したいと思います。まず、コメントアウトした# 初期値の推定より上ですが、始めに最後の結果を書き出すファイルの用意(ファイルの作成とインデックスの書き込み)をしています。そして、for文以下でデータファイルのリストを使ってイテレーションを開始しています。
match = re.match('(.*).dat', filename)
name = match.group(1)
のところは、最後に画像を書き出す時のファイル名用に.datの拡張子前の文字列をnameで抜き出しています。
次は# 初期値の推定のところです。今回のフィッティングで初期パラメータ(pini)として必要なのは、ピーク強度(intensity)、ピークを取るときのX(X0)、半値半幅(HWHM)です。どのくらいの精度で推定しておくかというのが難しいんですが、ここではそれぞれ以下のように推定しています。
推定していく順番に、
intensity:Yの最大値・最小値を取り出し、絶対値が大きい方を採用
X0:採用したintensityが出るときのXの値を採用
HWHM:推定してません。とりあえず1にしています。上2つのパラメータはだいぶ正確なのでここは妥協して良さそうです。
そして、# フィッティングのところ。推定した初期パラメータを用いてフィッティングします。ここはSciPyのフィッティング手順に沿ってフィッティングをしています。収束したパラメーターはpoptに格納されます。perrは標準誤差です。フィッティングパラメーターの共分散pcovの対角成分のルートを取っています。
参考:
・Pythonで非線形関数モデリング
・scipy.optimize.curve_fit(SciPyの公式ドキュメント)
最後は# 結果の表示と# datファイルへのフィッティング結果の書き込み、# フィッティング曲線描画用の配列を作成、# 結果のプロットと画像の保存です。# 結果の表示と# datファイルへのフィッティング結果の書き込みはそのままなので省略します。# フィッティング曲線描画用の配列を作成は、収束したパラメーターを使って定義した関数にデータのXを代入した結果です。なのでここではフィッティングラインのデータを元データと同じ点数で用意しています。# 結果のプロットと画像の保存もそのままなので省略します。
plt.savefig(name + ".png")
一応このようにして最初のre.matchの結果であるnameを使っています。
5. 結果
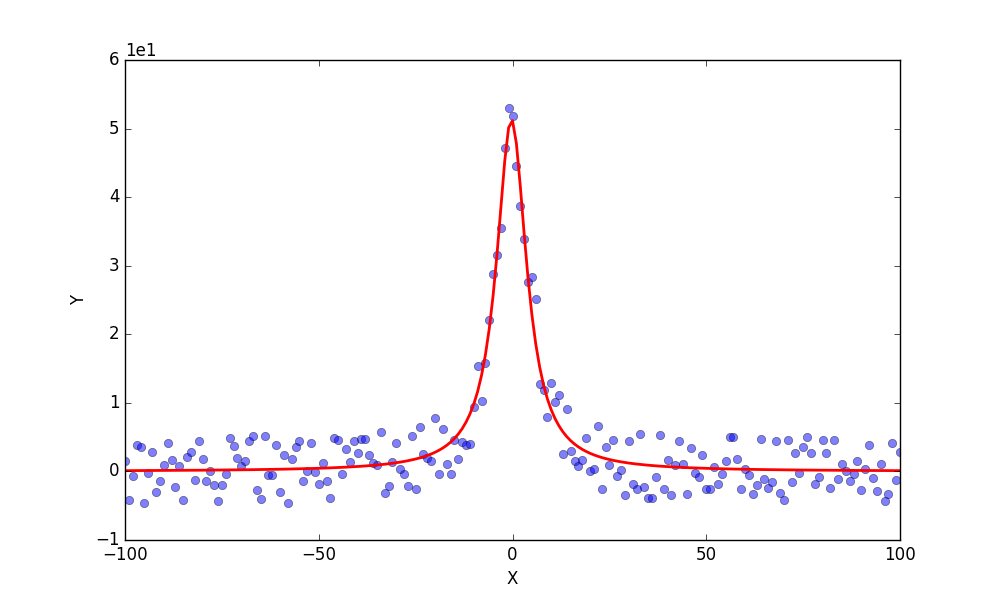
フィッティング結果の画像の方はこんな感じです。
そして、数値としての結果(収束したフィッティングパラメータと標準誤差をタブ区切りでまとめたもの)はfitresult.datに書き出されます。
6. おわりに
ということで、めでたく7つのファイルを一括でフィッティングすることができました。今回は簡単のため7つでしたが、まあ実験をやっていると数十から場合によっては百を超えるようなデータをフィッティングしないといけない時もあるので、そういう時には力を発揮すると思います。
7. 補足
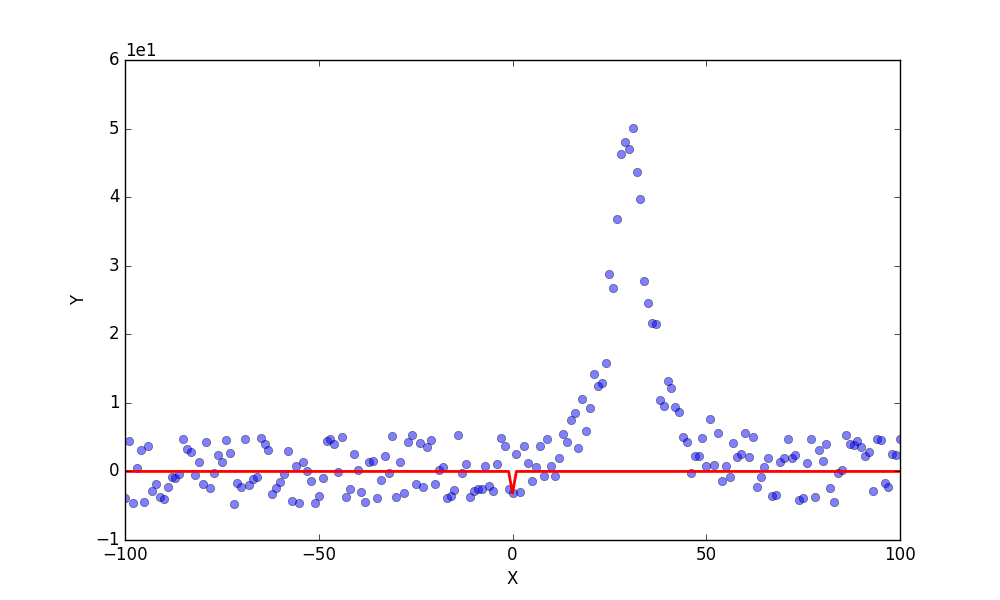
このくらいピークが明瞭なら、初期パラメータなんて全部適当に固定してしまってもうまくやってくれるんじゃないの?って思う人もいると思います。ただ、初期パラメータにオーダーレベルでずれがあると、
みたいなことになるのが実情です。線形フィッティングとかだと初期値の推定は必要ないと思いますが、やや関数が複雑になれば、ある程度(オーダーを見積もる程度でいいので)初期値を推定させた方が良さそうです。
Jupyterに馴染みがない方もいるかもしれないので、最後に.pyの形にしたものも置いておきます。
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize
import glob, re
from functools import cmp_to_key
filelist = glob.glob('X0=*.dat')
filelist2 = []
'''
/////////////////////////////////
データファイルのソート
/////////////////////////////////
'''
for filename in filelist:
match = re.match('X0=(.*).dat', filename)
tuple = (match.group(1), filename)
filelist2.append(tuple)
def cmp(a, b):
if a == b: return 0
return -1 if a < b else 1
def cmptuple(a, b):
return cmp(float(a[0]), float(b[0]))
filelist = [filename[1] for filename in sorted(filelist2, key=cmp_to_key(cmptuple))]
'''
/////////////////////////////////
解析(ローレンチアンフィッティング)
/////////////////////////////////
'''
result = open('fitting_result.dat', 'w')
result.writelines("filename\tA\tA_err\tX0\tX0_err\tHWHM\tHWHM_err\n")
for filename in filelist:
print(filename)
match = re.match('(.*).dat', filename)
name = match.group(1)
with open(filename, 'r') as file:
X, Y = [], []
for line in file.readlines()[1:]:
items = line[:-1].split('\t')
X.append(float(items[0]))
Y.append(float(items[1]))
# 初期値の推定(強度と中心値)
max_Y = max(Y)
min_Y = min(Y)
if np.abs(max_Y) >= np.abs(min_Y):
intensity = max_Y
X0 = X[Y.index(max_Y)]
else:
intensity = min_Y
X0 = X[Y.index(min_Y)]
# 初期値の設定
pini = np.array([intensity, X0, 1])
# フィッティング
def func(x, intensity, X0, HWHM):
return intensity * HWHM**2 / ((x-X0)**2 + HWHM**2)
popt, pcov = scipy.optimize.curve_fit(func, X, Y, p0=pini)
perr = np.sqrt(np.diag(pcov))
# 結果の表示
print("initial parameter\toptimized parameter")
for i, v in enumerate(pini):
print(str(v)+ '\t' + str(popt[i]) + ' ± ' + str(perr[i]))
# datファイルへのフィッティング結果の書き込み
result.writelines(name + '\t' + '\t'.join([str(p) + '\t' + str(e) for p, e in zip(popt, perr)]) + '\n')
# フィッティング曲線描画用の配列を作成
fitline = []
for v in X:
fitline.append(func(v, popt[0], popt[1], popt[2]))
# 結果のプロットと画像の保存
plt.clf()
plt.figure(figsize=(10,6))
plt.plot(X, Y, 'o', alpha=0.5)
plt.plot(X, fitline, 'r-', linewidth=2)
plt.xlabel('X')
plt.ylabel('Y')
plt.ticklabel_format(style='sci',axis='y',scilimits=(0,0))
plt.savefig(name + ".png")
plt.close()
result.close()