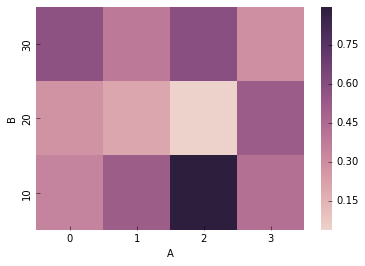More than 5 years have passed since last update.

Python / pandasのDataFrameで実験データ解析（物理屋さん、工学屋さん向け）

Last updated at 2019-10-24Posted at 2017-11-19

入門的内容ですが、Pythonを使った実験データ解析で役立ちそうなことをまとめます。
ひとまず、この記事では .DAT（タブ区切テキスト）と .CSV（カンマ区切りテキスト）のデータ形式を想定しています。
Jupyter Notebookというデータ分析ツールを使って、その中でPythonを実行します。

##使うデータ

A	B	C	D	E	F
0	10	100	0.3397403	0.271961552	0.81641005
0	20	100	0.279387916	0.044766148	0.697225701
0	30	100	0.571652671	0.285617692	0.426593025
1	10	100	0.51857147	0.420683546	0.660718825
1	20	100	0.198629043	0.008840571	0.080974462
1	30	100	0.382744217	0.522728466	0.676155085
2	10	100	0.89595261	0.723349138	0.230220379
2	20	100	0.03734517	0.956693623	0.008328477
2	30	100	0.587849709	0.171905051	0.31492908
3	10	100	0.425369125	0.008548215	0.590672961
3	20	100	0.520533453	0.77229485	0.647684286
3	30	100	0.290317035	0.608319517	0.8632759

A, B, C が測定条件、D, E, F が測定値（ここではただの乱数ですが…）みたいなイメージです。このデータをタブ区切りで保存したものをtable.dat、カンマ区切りで保存したものをtable.csvとします。

##ライブラリの読み込み

In[1]

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize
%matplotlib inline

##データの読み込み

CSVの場合

In[2]

df = pd.read_csv('table.csv')
df

DATの場合

In[2]

df = pd.read_table('table.dat')
df

読み込んだ結果

Out[2]

	A	B	C	D	E	F
0	0	10	100	0.339740	0.271962	0.816410
1	0	20	100	0.279388	0.044766	0.697226
2	0	30	100	0.571653	0.285618	0.426593
3	1	10	100	0.518571	0.420684	0.660719
4	1	20	100	0.198629	0.008841	0.080974
5	1	30	100	0.382744	0.522728	0.676155
6	2	10	100	0.895953	0.723349	0.230220
7	2	20	100	0.037345	0.956694	0.008328
8	2	30	100	0.587850	0.171905	0.314929
9	3	10	100	0.425369	0.008548	0.590673
10	3	20	100	0.520533	0.772295	0.647684
11	3	30	100	0.290317	0.608320	0.863276

データがpandasのDataFrameというオブジェクトで、名前はdfとして読み込まれました。
Jupyter内ではdfと打つことで、データが表として表示されます。
ヘッダーなど読み飛ばしたい行があるときは、オプションskiprowを付けて下のようにやります。

df = pd.read_table('table.dat', skiprows=5) #先頭5行読み飛ばし

他にも読み込み時のオプションは沢山用意されているので、詳しくはpandasの公式ドキュメントをどうぞ。
（上手く使えばファイルから必要なデータだけ効率的に読み込むことができます。）
https://pandas.pydata.org/pandas-docs/stable/api.html#flat-file

※ 以降の作業を辿りたい方は、次のコードで同じDataFrameを作ってください。

読み込みの代わりに実行

df = pd.DataFrame({'A': [0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3],
                   'B': [10, 20, 30, 10, 20, 30, 10, 20, 30, 10, 20, 30],
                   'C': [100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100],
                   'D': [0.3397403, 0.2793879, 0.5716526, 0.5185714, 0.1986290, 0.3827442, 0.8959526, 0.0373451, 0.5878497, 0.4253691, 0.5205334, 0.2903170],
                   'E': [0.2719615, 0.0447661, 0.2856176, 0.4206835, 0.0088405, 0.5227284, 0.7233491, 0.9566936, 0.1719050, 0.0085482, 0.7722948, 0.6083195],
                   'F': [0.8164100, 0.6972257, 0.4265930, 0.6607188, 0.0809744, 0.6761550, 0.2302203, 0.0083284, 0.3149290, 0.5906729, 0.6476842, 0.8632759]})

##カラムの指定

DataFrame の中でカラム（列）を指定する方法は大きく２つあります。
例えば今のデータでA列を指定したいときには、df.A もしくは、df['A'] と書きます。
カラム名に半角スペースなどが入っている時には、前者の記法は使えないので、後者で書くことになります。
また、DataFrameに新しくカラムを作成するときにも前者の記法は使えません。

##データ解析いろいろ

###指定した条件でデータを取り出し、プロットしてみる
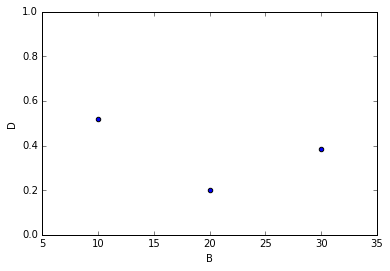
● 例えば A=1 の時の結果は・・・？

In[3]

df[df.A == 1]

Out[3]

	A	B	C	D	E	F
3	1	10	100	0.518571	0.420684	0.660719
4	1	20	100	0.198629	0.008841	0.080974
5	1	30	100	0.382744	0.522728	0.676155

A=1 の行はこうやって取り出せるので、次のようにして

In[4]

df[df.A == 1].plot(kind='scatter', x='B', y='D', logy=False, ylim=[0, 1], marker='o')

A=1 の時の B vs D の関係をプロットできます。
もちろん条件式のところは不等式でも構いません。
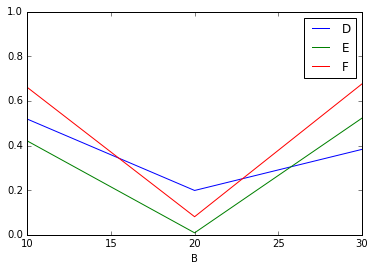
他にも、A=1 の時のデータから複数列選択して、

In[5]

df[df.A == 1].plot(x='B', y=['D', 'E', 'F'], logy=False, ylim=[0, 1])

B に対する D, E, F の変化を比較したり。色々できます。
グラフの詳しい説明については Pandas の公式ドキュメントをどうぞ。
https://pandas.pydata.org/pandas-docs/stable/visualization.html#plotting-directly-with-matplotlib

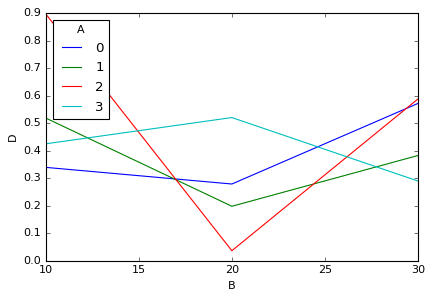
A の値で系列分けして B vs D をプロット

B に対して A = 0, 1, 2, 3 の時の D をそれぞれ別系列でグラフ化したい時は、

In[6]

df_pivot = pd.pivot_table(data=df, values='D', columns='A', index='B', aggfunc=np.mean)
df_pivot

Out[6]

A	0	1	2	3
B				
10	0.339740	0.518571	0.895953	0.425369
20	0.279388	0.198629	0.037345	0.520533
30	0.571653	0.382744	0.587850	0.290317

このようにピボットテーブルを作成すれば、

In[7]

df_pivot.plot()
plt.ylabel('D')

A の値で系列分けできます。
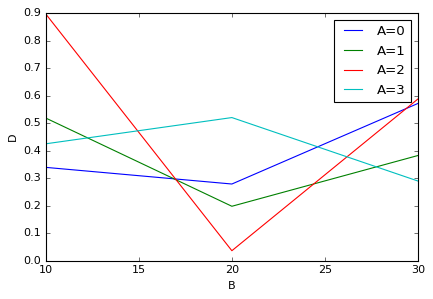
でも、レジェンドがいまいちだな…。「A=0, A=1,...」と書きたいなと思ったら、下のようにカラム名を書き換えます。

df_pivot.columns = ['A=' + str(A) for A in df_pivot.columns.tolist()]

###フィッティングしてみる
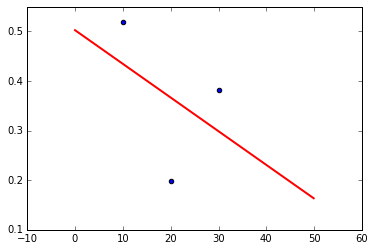
● 例えば先程の A=1 の時の B vs D を一次関数でフィッティングするには・・・

In[8]

def func(x, a, b):
    return a * x + b

pini = np.array([1, 1]) #パラメータa, bの初期値
popt, pcov = scipy.optimize.curve_fit(func, df[df.A == 1].B, df[df.A == 1].D, p0=pini)
perr = np.sqrt(np.diag(pcov))

# 結果の出力
print('initial parameter\toptimized parameter')
for i, v  in enumerate(pini):
    print(str(v)+ '\t' + str(popt[i]) + ' ± ' + str(perr[i]))

#グラフの表示
X = np.arange(0, 50, 0.1)
fit_line = func(X, popt[0], popt[1])
plt.plot(X, fit_line, 'r-', linewidth=2)
plt.scatter(df[df.A == 1].B, df[df.A == 1].D)

Out[8]

initial parameter	optimized parameter
1	-0.0067913626522 ± 0.0145508894248
1	0.502475496332 ± 0.314335138397

ここでは初期のパラメータpiniと、収束したパラメータpoptを書き出しています。
標準誤差perrは共分散pcovの対角成分のルートです。
書き出し方は適当にアレンジしてみてください。

###データを演算してみる
● 例えば新しく列 G を G = D + 2 * E + exp(F) として作りたい時は・・・

In[9]

df['G'] = df['D'] + 2 * df['E'] + np.exp(df['F']) 
df

Out[9]

	A	B	C	D	E	F	G
0	0	10	100	0.339740	0.271962	0.816410	3.146027
1	0	20	100	0.279388	0.044766	0.697226	2.377094
2	0	30	100	0.571653	0.285618	0.426593	2.674917
3	1	10	100	0.518571	0.420684	0.660719	3.296122
4	1	20	100	0.198629	0.008841	0.080974	1.300653
5	1	30	100	0.382744	0.522728	0.676155	3.394504
6	2	10	100	0.895953	0.723349	0.230220	3.601528
7	2	20	100	0.037345	0.956694	0.008328	2.959096
8	2	30	100	0.587850	0.171905	0.314929	2.301822
9	3	10	100	0.425369	0.008548	0.590673	2.247668
10	3	20	100	0.520533	0.772295	0.647684	3.976233
11	3	30	100	0.290317	0.608320	0.863276	3.877871

とやります。一番右に列 G ができました。
関数についての詳しい話は、numpyの公式ドキュメントをどうぞ。
https://docs.scipy.org/doc/numpy-1.13.0/reference/routines.math.html

何度も使うような処理の場合は関数を定義してやると見通しがよくなります。

In[9]と同じ処理

def cal_G(d, e, f):
    g = d + 2 * e + np.exp(f)
    return g

df['G'] = cal_G(df['D'], df['E'], df['F'])
df

差分を取る

● 後退差分
新しくカラム diff_A を diff_A[i] = A[i] - A[i-1] として定義、追加したい時は、DataFrame の diff メソッドを使います。

df['diff_A'] = df.A.diff() #次の前進差分と対応付けるため明示的に書くと、これは df.A.diff(1) です。

定義から明らかですが、diff_A[0]はA[-1]が存在しないので定義できません。NaNになります。

● 前進差分
diff_A を diff_A[i] = A[i+1] - A[i] として定義、追加したい時は、同じく diff メソッドを使って、

df['diff_A'] = df.A.diff(-1)

と書きます。この場合は最後の要素が定義されず、NaNになります。

● 中心差分
diff_A を diff_A[i] = A[i+1] - A[i-1] として定義、追加したい時はカラムをシフトさせて計算します。

df['diff_A'] = df.A.shift(-1) - df.A.shift(1)

この場合は最初と最後の要素が定義されず、NaNになります。

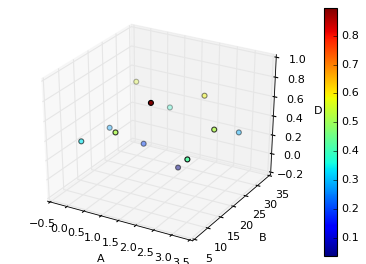
A, B vs D で 3D プロットを作ってみる

In[10]

from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
scatter = ax.scatter(df.A, df.B, df.D, c=df.D)
plt.colorbar(scatter) 
ax.set_xlabel('A')
ax.set_ylabel('B')
ax.set_zlabel('D')

今回のデータ構造だと 3D プロットはそのまますぐに作れます。
3D プロットは他にも色々種類があるので、詳しくはmatplotlibの公式ドキュメントをどうぞ。
https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html

A, B vs D でカラープロットを作ってみる

上の方で作ったピボットテーブルからカラープロットも作ることができます。
一部繰り返しになりますが、もう一度書くと、

In[11]

df_pivot = pd.pivot_table(data=df, values='D', columns='A', index='B', aggfunc=np.mean)
plt.pcolor(df_pivot)
plt.yticks(np.arange(0.5, len(df_pivot.index), 1), df_pivot.index)
plt.xticks(np.arange(0.5, len(df_pivot.columns), 1), df_pivot.columns)
plt.colorbar()
plt.xlabel('A')
plt.ylabel('B')

カラープロットができました。
色とかデザインがダサいと思った時には、

In[12]

import seaborn as sns
sns.heatmap(df_pivot[::-1], cmap=sns.cubehelix_palette(as_cmap=True))
plt.xlabel('A')
plt.ylabel('B')

seabornっていうパッケージを使うと、お洒落なグラフになったりします。
seabornの詳しい話は公式ドキュメントをどうぞ。
http://seaborn.pydata.org/examples/index.html

結果の保存

DataFrame を csv として保存するには・・・

df.to_csv('table2.csv')

.to_csv()という DataFrame のメソッドを使います。
書き出したい DataFrame にくっつけてください。

グラフを画像として保存するには・・・

plt.savefig('image.png')

これ単独では意味が無いので、グラフを表示させたセルの最後に追記してください
（例えばIn[11]の最後とか）。拡張子は png, jpg, eps, pdf などが使えます。
書き出し時のファイル名で指定すれば勝手にその形式で書き出されます。

おまけ：イテレーションで楽する

ここまで簡単なデータ解析とグラフ化について書いてきましたが、これらの作業を複数のファイルに渡って繰り返し実行する場合、次のようなイテレーションを組むと便利です。

こんな感じでデータがあったとき、globモジュールを使うことで、
（ここからJupyterは離れます）

>>> import glob
>>> filelist = glob.glob('*.dat')
>>> print(filelist)
['data_0.dat', 'data_1.dat', 'data_10.dat', 'data_11.dat', 'data_12.dat', 'data_13.dat', 'data_14.dat', 'data_15.dat', 'data_16.dat', 'data_17.dat', 'data_18.dat', 'data_19.dat', 'data_2.dat', 'data_20.dat', 'data_21.dat', 'data_22.dat', 'data_23.dat', 'data_24.dat', 'data_25.dat', 'data_26.dat', 'data_27.dat', 'data_28.dat', 'data_29.dat', 'data_3.dat', 'data_30.dat', 'data_31.dat', 'data_32.dat', 'data_33.dat', 'data_34.dat', 'data_35.dat', 'data_36.dat', 'data_37.dat', 'data_38.dat', 'data_39.dat', 'data_4.dat', 'data_40.dat', 'data_41.dat', 'data_42.dat', 'data_43.dat', 'data_44.dat', 'data_45.dat', 'data_46.dat', 'data_47.dat', 'data_48.dat', 'data_49.dat', 'data_5.dat', 'data_50.dat', 'data_6.dat', 'data_7.dat', 'data_8.dat', 'data_9.dat']

ワイルドカードを使ったファイルの検索とファイルのリスト化ができます。
よって、このリストを使ってイテレーションを組めば、

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize
import glob

filelist = glob.glob('*.dat')
for file in filelist:
    df = pd.read_table(file)
    #これまでに書いてきたような処理・・・

リストの中のファイルに対して順繰りに一定の処理を加えることができます。
globモジュールではパスごと引っ張ってこれるので、カレントディレクトリのフォルダ以下を

filelist = glob.glob('./*/*.dat')

のようにして検索することも可能です。同じようなグラフを何枚も描かないといけない、同じようなフィッティングを何度も行わないといけない、そういう時にはこの方法がとても有効です。

＊＊＊

学生実験にしろ研究にしろ、実験データの解析には面倒なことが多々ありますが、一度解析の方向性が決まれば、ほとんどのことは Python で自動化できます。Excelを開いてデータをペチペチ整形したり、ひたすら同じようなグラフを作ったり、そんな人間味のないルーチンワークからは是非開放されましょう！

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up