【地理空間データ】同時自己回帰モデルの概要と選択方法

はじめに

地理空間データの勉強を始めようとして、村上大輔さんの「Ｒではじめる地理空間データの統計解析入門」(2022年4月6日発売)を読み初めました。まだ半分しか読んでないですが、間違い無く良書なので、本の中で紹介されていた手法を使い手を動かしてみました。なお、書いているコードの9割は本書に記載されている物を使います。今回は同時自己回帰モデル(Simultaneous Autoregressive; SAR)と呼ばれる空間相関をモデルを紹介すると同時に、そのモデルの取捨選択方法に触れてみます。

同時自己回帰モデル(Simultaneous Autoregressive; SAR)

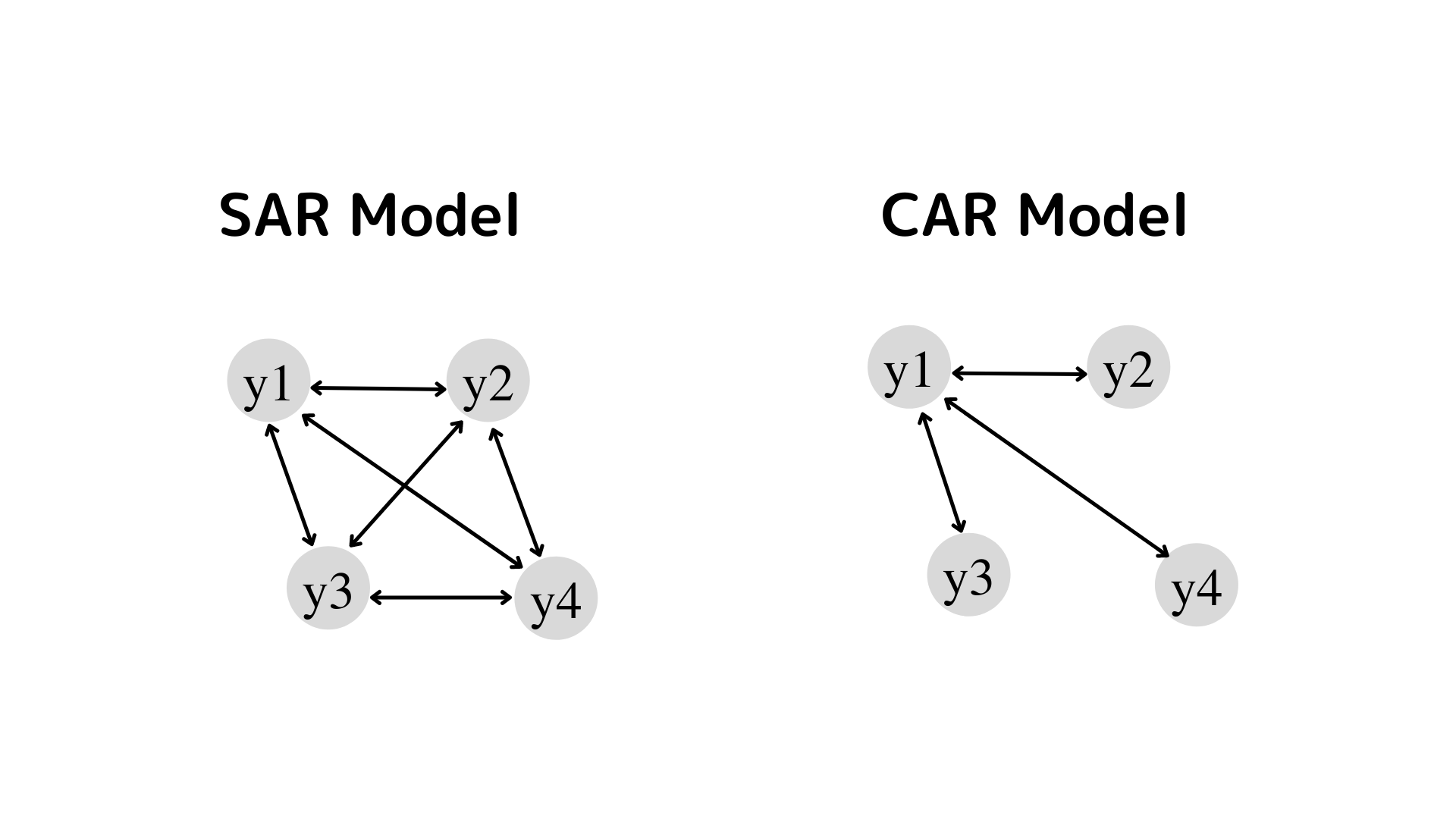
同時自己回帰モデル(Simultaneous Autoregressive; SAR)とはエリア間の空間相関関係を同時にモデル化するもので、同時多発的に各エリア同士が影響しあう空間相関性を仮定するものです。また、条件付き自己回帰モデル(Conditional Autoregressive; CAR)とは１エリアの観測値が周りのエリアの影響を受けていると仮定します。エリア同士の同時多発的相互作用は考慮されません。

式

$\boldsymbol{W}$ は空間の相関の強さを表し、空間重み行列(Spatial Weight Matrix) と呼ばれます。

$$
y_i = \rho \boldsymbol{Wy} + \beta_01 + \epsilon \qquad \epsilon \sim N(0,\boldsymbol{I})
$$
$$
y =
\begin{bmatrix}
y_1 \\
y_2 \\
\vdots \\
y_N \\
\end{bmatrix} \qquad \boldsymbol{W}=
\begin{bmatrix}
0 & w_{1,2}& \dots & w_{1,N} \\
w_{2,1} &0&\dots & w_{2,N} \\
\vdots & \vdots & \ddots & \vdots \\
w_{N,1} & w_{N,2} & \dots & 0 \\
\end{bmatrix} \qquad \boldsymbol{1}=
\begin{bmatrix}
1 \\
1 \\
\vdots \\
1 \\
\end{bmatrix} \qquad \epsilon=
\begin{bmatrix}
\epsilon_1 \\
\epsilon_2 \\
\vdots \\
\epsilon_N \\
\end{bmatrix}
$$

直接効果・間接効果

同一エリア内での説明変数の影響を表すのが 直接効果（direct effect) で、上記式中のマトリックスの対角要素になります。「エリア$i$の説明変数$x_{i,k}$が１単位増加した時のエリア$j$の目的変数の変化量」である$\dfrac{\partial y_j}{\partial x_{i,k}}$は間接効果（indirect effect） と呼ばれます。上記式中のマトリックスの非対角要素になります。

モデル

SARモデルはどれに空間相関を仮定するかで使うモデルが違います。以下の表を参照して見てください。

モデル	目的変数	説明変数	誤差項($\epsilon$)
空間ラグモデル(SLM)	○
SLXモデル		○
空間エラーモデル(SEM)			○
空間ダービンモデル(SDM)	○	○
空間ダービンエラーモデル(SDEM)		○	○
SARARモデル	○		○
Manskiモデル	○	○	○

実装

上記で説明しただけでは、どのモデルを使うと良いか、いまいちピントきにくいかもしれません。そこで、spatialregライブラリを用い、どのモデルを使えばいいかを検定してみたいと思います。
ここでも「Ｒではじめる地理空間データの統計解析入門」(2022年4月6日発売)で紹介された例を用いRで実装していきます。

データ

使うデータはおなじみ、ボストン住宅価格データを使用します。データの概要はこのようになっています。目的変数はMEDV（住宅価格の中央値）になります。

モデル

必要ライブラリをインストールします。

setup

library(spatialreg)
library(spdep)
library(car)
data(boston)

boston.soiは同データセットをnb型（neighboursの略称で空間近接情報のデータ型）にしたものです。これを以下のコマンドで空間重み行列に変換します。

w = nb2listw(boston.soi)

モデル式を生成、前回の記事でモデルに大きな影響を与えるとされた3つの説明変数に指定します。

formula = CMEDV ~ LSTAT + RM + CRIM

回帰モデル

まず、回帰モデルを作成し、空間相関を仮定したモデルとの優位性を測定します。

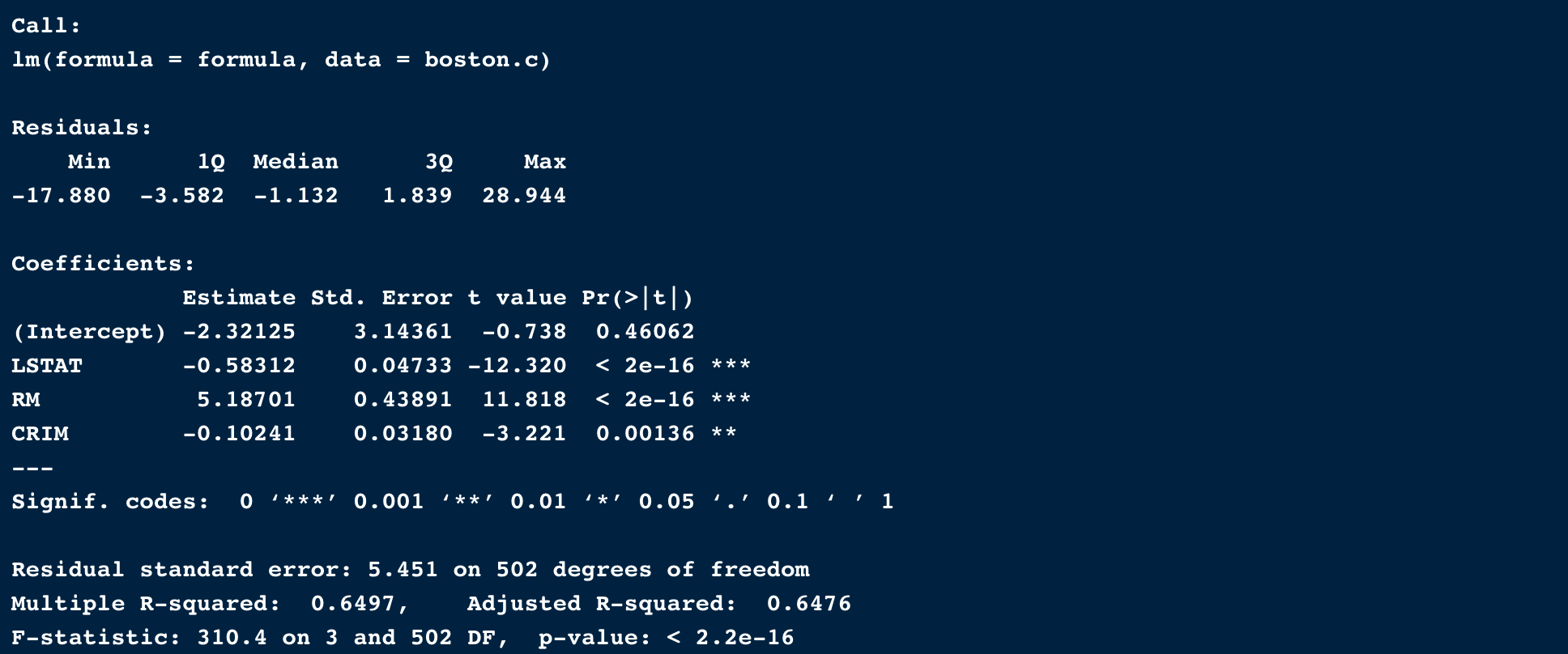
lmod = lm(formula, data = boston.c)
summary(lmod)

取捨選択

さて、いよいよ、最適な空間相関モデルを選択していきます。今回は目的変数と誤差項に空間相関を仮定するので空間ラグモデル(SLM)か空間エラーモデル(SEM)のどちらを使うべきか検証していきます。どちらも使うべきではないとされた場合は、空間相関が無いものとし、上記の回帰モデルが適用されます。具体的には以下のような手順で進めていきます。

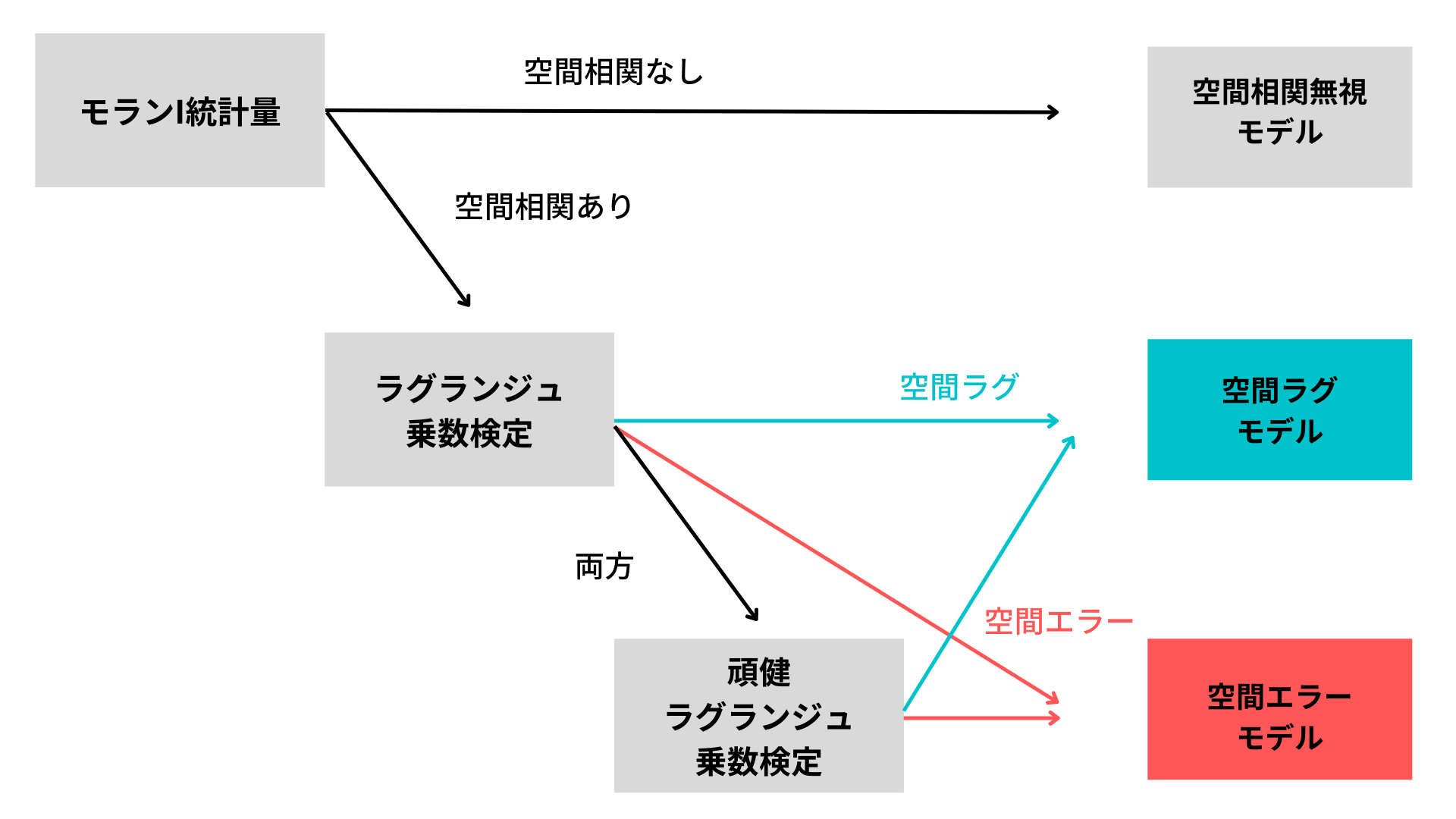
モランI統計量

モランI統計量で回帰モデルと、空間相関を仮定したモデルとの優位性を測定します。

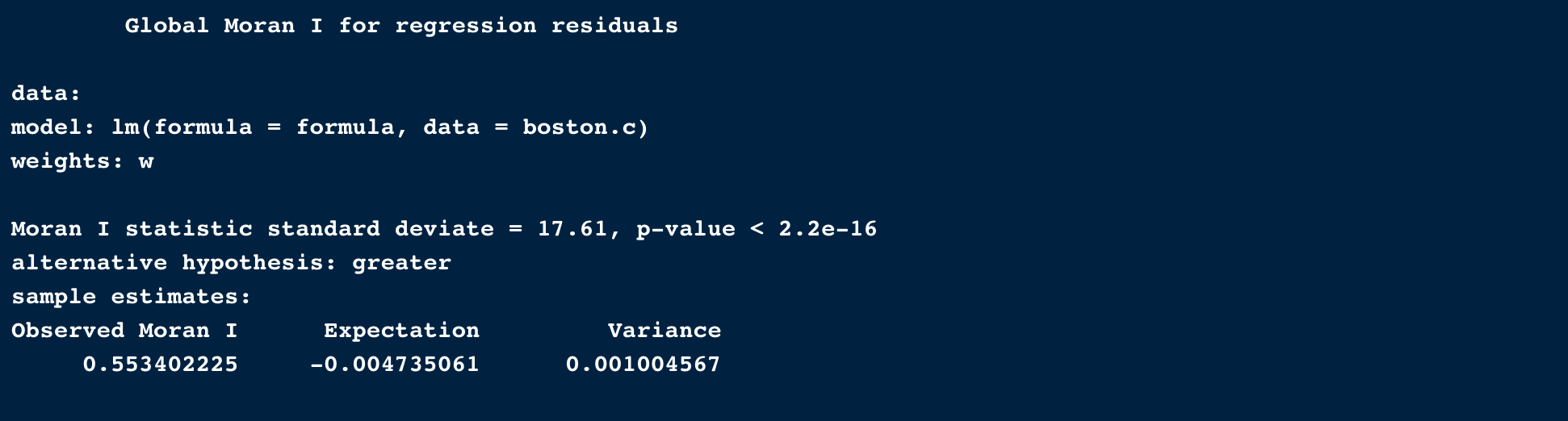
lm.morantest(lmod, w)

Moran I statistic standard deviate のp値が0.05以下なので、5%の水準で空間相関が残差に存在することが証明されました。つまり、「空間相関を加味したモデルを使うべき」 との事です。

ラグランジュ乗数検定（Lagrange Multiplier Tests）

ラグランジュ乗数検定（Lagrange Multiplier Tests）は空間ラグモデル(LMlag)と空間エラーモデル(LMerr)に対する有意差検定を行うものでlm.LMtestsメソッドで実行できます。

lm.LMtests(lmod, w, test = c('LMlag', 'LMerr')) %>% 
  summary()

上記の結果より、空間ラグモデル(LMlag)と空間エラーモデル(LMerr)の両方が回帰モデルより支持されている事がわかります。（p値が両方水準以上だった場合は空間相関を仮定しないモデルが支持されることになります）

頑健ラグランジュ乗数検定（Robust Lagrange Multiplier Tests）

頑健ラグランジュ乗数検定（Robust Lagrange Multiplier Tests）とは空間ラグモデルで仮定する目的変数(RLMlag)と空間エラーモデル(RLMerr)で仮定する誤差項のうち、片方の空間相関を無視し検定する事で、両モデルの優位性を検定するものです。これもlm.LMtestsで実行できます。

lm.LMtests(lmod, w, test = c('RLMlag', 'RLMerr')) %>% 
  summary()

両モデルが0.05水準で支持されていますが、パラメーターを確認すると、空間エラーモデル(RLMerr)が強く支持されている事がわかります。よって、空間エラーモデルを使いモデルを組む立てると良いとされます。

おわりに

村上大輔さんの「Ｒではじめる地理空間データの統計解析入門」で紹介されている、空間相関モデルの紹介とモデルの選択の仕方についてまとめました。今回はモデルの特性上、目的変数と誤差項に空間相関を想定したため、モランI統計量、ラグランジュ乗数検定、頑健ラグランジュ乗数検定を用い、空間相関モデルの取捨選択方法についてまとめました。

参考文献