二分探索木
- 二分探索を木構造でやる
- 配列を用いた二分探索だと,探索は$O(\log_2 n)$で実行できるが,データの挿入・削除は配列の性質から,$O(n)$かかってしまう
- (左右にバランスのとれた)二分木を用いた二分探索だと,探索・挿入・削除全て$O(\log_2 n)$で行うことができる
探索・挿入
- 二分木の再帰的な構造を利用する
削除
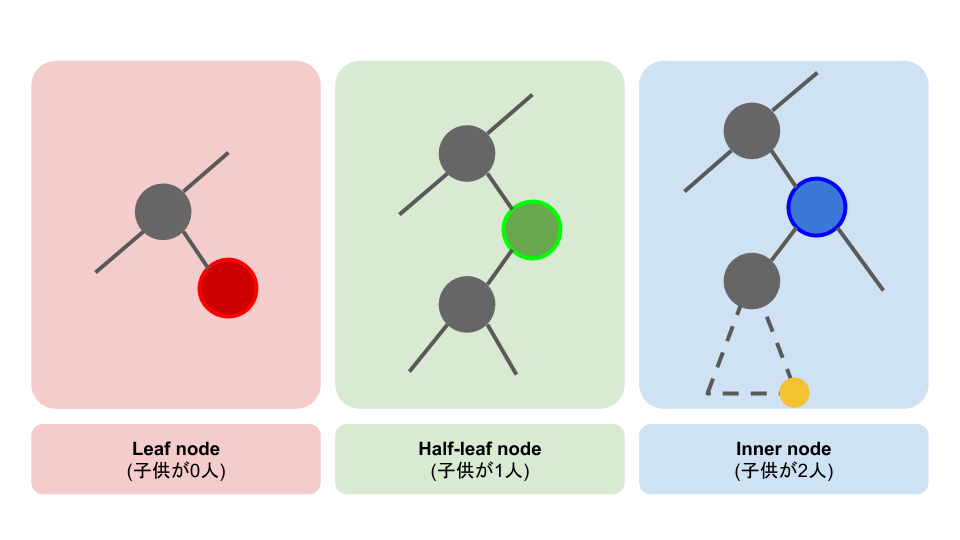
- 削除したいノードがいくつ子供を持っているかによって変わってくる
実装
package main
import (
"errors"
"fmt"
"log"
)
type Node struct {
Value string
Data string
Left *Node
Right *Node
}
// `Insert()` inserts a new data into the tree, at the position which is determined by the inserted value.
//
// 1. Start at the root node.
// 2. Compare the new value with the current node's value...
// - If it is the same, stop. We have that value already.
// - If it is smaller, repeat 2. with the left child node. If there is no left child node, then add a new one with the new value and stop.
// - If it is greater, repeat 2. with the right child node. If there is no right child node, then add a new one with the new value and stop.
func (n *Node) Insert(value, data string) error {
if n == nil {
return errors.New("Cannot insert a value into a nil tree")
}
switch {
case value == n.Value:
return nil
case value < n.Value:
if n.Left == nil {
n.Left = &Node{Value:value, Data:data}
return nil
}
return n.Left.Insert(value, data)
case value > n.Value:
if n.Right == nil {
n.Right = &Node{Value:value, Data: data}
return nil
}
return n.Right.Insert(value, data)
}
return nil
}
// `Search()` searches the given data from the tree.
func (n *Node) Search(s string) (string, bool) {
if n == nil {
return "", false
}
switch {
case s == n.Value:
return n.Data, true
case s < n.Value:
return n.Left.Search(s)
default:
return n.Right.Search(s)
}
}
// `findMax()` finds the maximum element in a (sub-)tree and returns the node itself and its parent node.
func (n *Node) findMax(parent *Node) (*Node, *Node) {
if n == nil {
return nil, parent
}
if n.Right == nil {
return n, parent
}
return n.Right.findMax(n)
}
// `replace()` replaces the `parent`'s child pointer to `n` with a pointer to the `replacement`node.
func (n *Node)replace(parent, replacement *Node) error {
if n == nil {
return errors.New("`replace()` is not allowed on a nil node")
}
if n == parent.Left {
parent.Left = replacement
return nil
}
parent.Right = replacement
return nil
}
// `Delete()` deletes the given element from the tree.
// It is an error to try deleting an element that does not exist in the tree.
// In order to remove an element properly, `Delete` needs to know the to-be-deleted node's parent.
//
// Delete
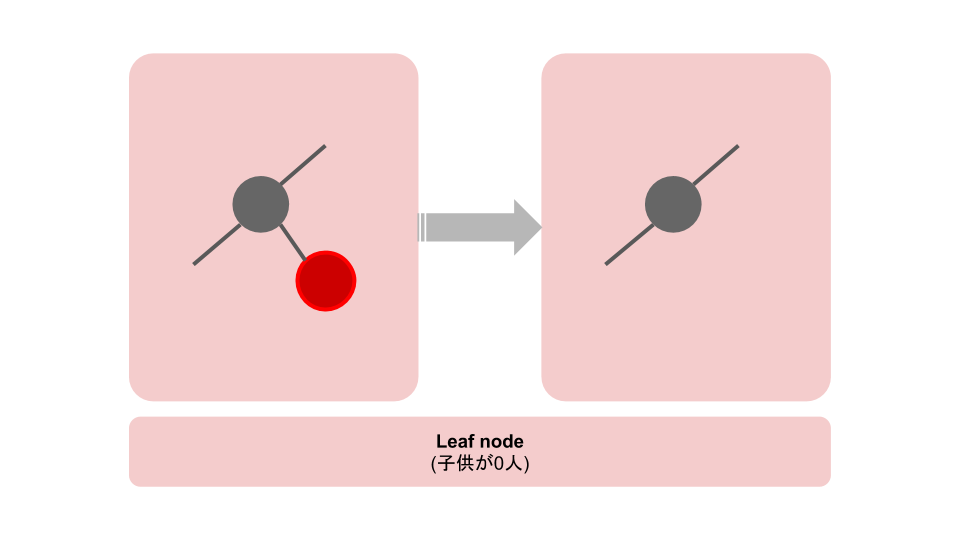
// 1. Delete a leaf node.
// - Just set the parent's child pointer to `nil`
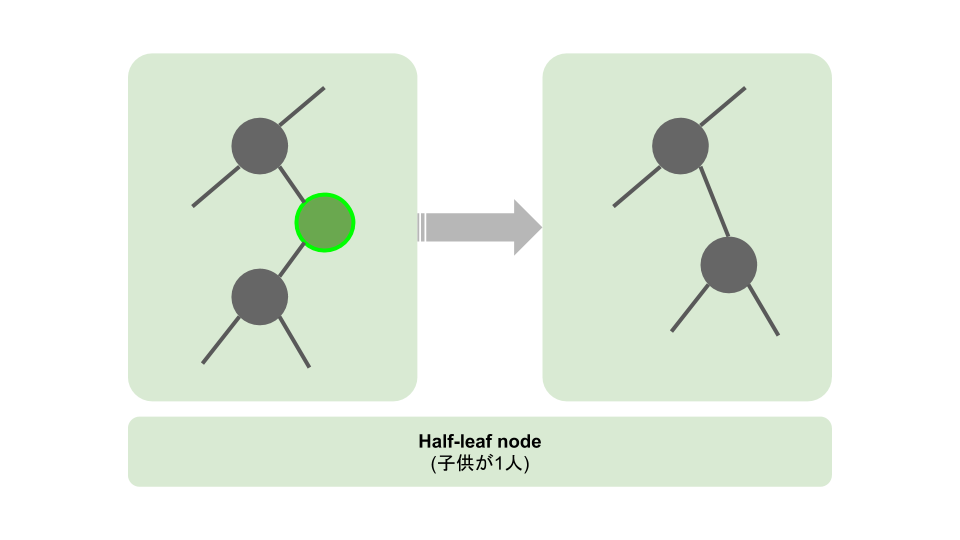
// 2. Delete a half-lead node.
// - Just replace the node by its child node.
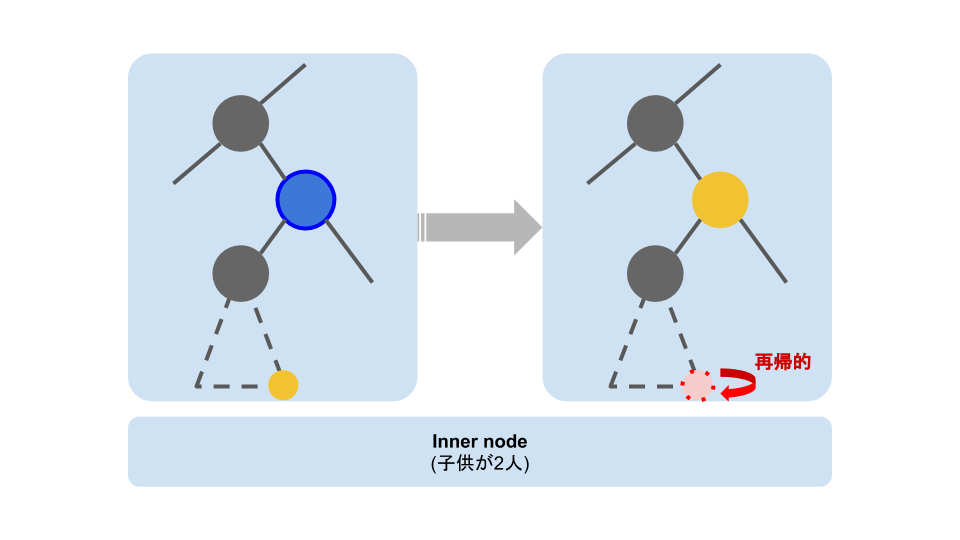
// 3. Delete an inner node.
// - The to-be-deleted node has two children, and we cannot assign both to the to-be-deleted node's parent node.
// - In the to-be-deleted node's left subtree, find the node with the largest value. Let me call this "Node A"
// - Replace the to-be-deleted node's value with A's value.
// - If A is a leaf node or a half-leaf node, delete Node A as described above for the leaf and half-leaf cases.
// - If A is an inner node, recursively call this `Delete()` on this node.
func (n *Node) Delete(s string, parent *Node) error {
if n == nil {
return errors.New("Value to be deleted does not exist in the tree")
}
switch {
case s < n.Value:
return n.Left.Delete(s, n)
case s > n.Value:
return n.Right.Delete(s, n)
default:
// We find the to-be-deleted node.
// If the node has no children, just remove it from its parent.
if n.Left == nil && n.Right == nil {
n.replace(parent, nil)
return nil
}
// If the node has one children, replace the node with its child.
if n.Left == nil {
n.replace(parent, n.Right)
return nil
}
if n.Right == nil {
n.replace(parent, n.Left)
return nil
}
// If the node has two children, we have to find the node which has the maximum value, in the left subtree of the to-be-deleted node.
replacement, replParent := n.Left.findMax(n)
// Replace the node's value.
n.Value = replacement.Value
n.Data = replacement.Data
// Remove the replaced node.
return replacement.Delete(replacement.Value, replParent)
}
}
type Tree struct {
Root *Node
}
func (t *Tree) Insert(value, data string) error {
if t.Root == nil {
t.Root = &Node{Value:value, Data:data}
return nil
}
return t.Root.Insert(value, data)
}
func (t *Tree) Search(s string) (string, bool) {
if t.Root == nil {
return "", false
}
return t.Root.Search(s)
}
func (t *Tree) Delete(s string) error {
if t.Root == nil {
return errors.New("Cannot delete from an empty tree")
}
// We have to call `Delete()` with fake node in order to avoid having to treat the root node as a special case.
fakeRoot := &Node{Right: t.Root}
err := t.Root.Delete(s, fakeRoot)
if err != nil {
return err
}
// If the root node is the only node in the tree and if it is deleted, `t.Root` still points to the old node, so we have to rectify this by setting `t.Root` to `nil`.
if fakeRoot.Right == nil {
t.Root = nil
}
return nil
}
func (t *Tree) PreorderTraverse(n *Node, f func(*Node)) {
if n == nil {
return
}
f(n)
t.PreorderTraverse(n.Left, f)
t.PreorderTraverse(n.Right, f)
}
func (t *Tree) InorderTraverse(n *Node, f func(*Node)) {
if n == nil {
return
}
t.InorderTraverse(n.Left, f)
f(n)
t.InorderTraverse(n.Right, f)
}
func (t *Tree) PostorderTraverse(n *Node, f func(*Node)) {
if n == nil {
return
}
t.PostorderTraverse(n.Left, f)
t.PostorderTraverse(n.Right, f)
f(n)
}
func main() {
values := []string{"d", "b", "c", "e", "a"}
data := []string{"delta", "bravo", "charlie", "echo", "alpha"}
// Create tree
tree := &Tree{}
for i := 0; i < len(values); i++ {
err := tree.Insert(values[i], data[i])
if err != nil {
log.Fatal("Error inserting value `", values[i], "`: ", err)
}
}
// Inorder traverse from root
fmt.Print("Sorted values: | ")
tree.InorderTraverse(tree.Root,
func(n *Node) {
fmt.Print(n.Value, ": ", n.Data, " | ")
})
fmt.Println()
// Search
s := "d"
fmt.Print("Find node '", s, "': ")
d, found := tree.Search(s)
if !found {
log.Fatal("Cannot find '" + s + "'")
}
fmt.Println("Found " + s + ": '" + d + "'")
// Delete
err := tree.Delete(s)
if err != nil {
log.Fatal("Error deleting "+s+": ", err)
}
fmt.Print("After deleting '" + s + "': ")
tree.InorderTraverse(tree.Root,
func(n *Node) {
fmt.Print(n.Value, ": ", n.Data, " | ")
})
fmt.Println()
}
末尾再帰の除去
- よく見ると,二分探索木の
Search()とInsert()には末尾再帰がある - 末尾再帰は,必ず反復で書き下すことができる
- 末尾再帰とは「再帰の一形態」で,「再帰呼び出しの結果をそのまま返す」ような再帰を末尾再帰という
- ただの再帰で書かれた処理は,制御が呼び出し側に戻ってきた時点で行う計算を呼び出され側に押し込むように書き直すことができるならば,末尾再帰の形で書き改めることができて,これもこれで最適化の一つ
- さらに,末尾再帰で書かれた処理は,必ず反復で書き下すことができて,これを末尾再帰最適化(要するに末尾再帰の除去)と呼ぶ
- 言語処理系によって末尾再帰最適化が施されることがある.
- 参考:末尾再帰による最適化
procedure P(x);
begin
....
if ....
P(α) // Here is tail recursion!
else
....
end
procedure P(x);
label 1;
begin
1:
....
if ....
x := α
goto 1
else
....
end
-
例えば合計を計算する
sum()を(1)ただの再帰(2)末尾再帰(3)末尾再帰を除去していてレーティブに書いたやつ,でやってみる. -
ただの再帰
func sum(n int) int {
if n == 1 {
return 1
}
return sum(n-1) + n
}
- 末尾再帰
func sum(n, result int) int {
if n < 1 {
return result
}
return sum(n-1, result + n) // 計算自体を再帰的に呼ばれる次の関数(正体は自分自身)に委託してしまう
}
- 末尾再帰を除去してイテレーティブに
func sum(n, result int) int {
LOOP:
if n < 1 {
return result
}
result += n
n -= 1
goto LOOP
}
末尾再帰を除去した実装(Search()とInsert()だけ抜粋)
func (n *Node) Search(s string) (string, bool) {
var result, p *Node
p = n
for p != nil {
if s == p.Value {
result = p
p = nil
} else {
if s < p.Value {
p = p.Left
} else {
p = p.Right
}
}
}
if result == nil {
return "", false
} else {
return result.Data, true
}
}
- ここでいう
for p != nilに戻ってくることが,「再帰的に呼び出された関数の先頭にジャンプする」ことに対応する
func (n *Node) Insert(value, data string) error {
var parent *Node
current := n
if current == nil {
return errors.New("Cannot insert a value into a nil tree")
}
for current != nil {
parent = current
if value < current.Value {
current = current.Left
} else {
current = current.Right
}
}
if value < parent.Value {
parent.Left = &Node{Value:value, Data:data}
} else {
parent.Right = &Node{Value:value, Data:data}
}
return nil
}
- 入れるべき場所までポインタを降ろしていってそこに挿入する