概要
- 線形回帰モデルの最尤推定を実装する場合に、正規方程式を書くと思います(PRML3章など)
- 正規方程式を実装した場合に、(たぶん)逆行列の精度が悪く、推定結果の精度が悪い場合がある
- そこで、ムーア-ペンローズの擬似逆行列を使うと良いよ という話
正直なところ、何が原因かはっきりと理解できていないので、詳しい方教えてください。
[2021/11/30 追記]
速攻でコメントいただきましたし、Twitterでもご指摘いただきました。
以下に簡単にまとめておきますが、当たり前すぎて恥ずかしいす。
- 正規方程式で期待した解が得られない理由
- 実験の条件では、モデルの次数よりもデータが少ない
- そのため、逆行列がない
- だから正規方程式で解を求めようというのがそもそも間違い
- 疑似逆行列では期待したよな解が得られた
- 疑似逆行列ではコメントで頂いた通り、最小二乗法を利用して数値的に計算しているため、逆行列を求めるというようなことをしていない。
- そのため、合理的な解が得られた。
- 正規方程式で求めようとしていた逆行列は何?
- これはよくわかっていません(numpyでの逆行列の解法を調べておりません。。。)
わかってしまえば至極当然なので、ものすごく恥ずかしいわけですが、悩んでた時は考えが至らなかったんですよね。
そもそも、逆行列計算できてしまっていたので、逆行列が計算できない問題設定になっていることが頭から抜け落ちておりました。。。
環境
- ハード
- macOS Big Sur (11.4)
- Mac mini (M1, 2020)
- チップ Apple M1
- Python
- Python 3.9.5
- numpy 1.21.0
線形回帰の最尤推定解
モデルとしては以下の通り、普通の線形回帰モデルを考えます。
$$
y = \mathcal{N}(y | \mathbf{w}^{\top}\mathbf{\phi}(\mathbf{x}), \sigma^2)
$$
ここで今回は、特徴抽出関数$\phi_i(x)$は$x^{i}$の多項式を扱います。
導出は省きますが、計画行列$\Phi$を利用すると、最尤推定解は以下の通りとなります。
$$
\mathbf{w}_{MLE} = \left( \Phi^{\top} \Phi \right)^{-1} \Phi^{\top} \mathbf{y}
$$
これが正規方程式として知られているものです。
ここで、上記の正規方程式での以下の部分を行列$\Phi$のムーア-ペンローズの擬似逆行列(Moore-Penrose pseudo-inverse matrix)です。(本に書いてました)
$$
\Phi^{\dagger} \equiv \left( \Phi^{\top} \Phi \right)^{-1} \Phi^{\top}
$$
この$\Phi^{\dagger}$はnumpy.linalg.pinvとしてnumpyにて提供されています。
ということで、線形回帰のパラメータの最尤推定解は擬似逆行列を使って次のようにも書けます。
$$
\mathbf{w}_{MLE} = \Phi^{\dagger} \mathbf{y}
$$
numpyを使ってこの二つの挙動を確認してみます。
実装の詳細は、notebookを貼り付けておくのでご確認いただけたらと思います。
トイデータ
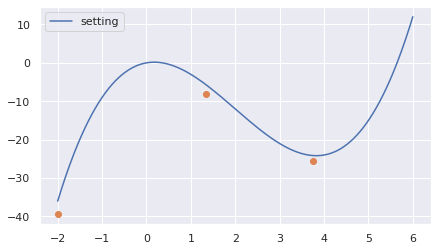
今回実験を行うにあたって、下図のデータを生成しました。
設定関数として、3次の多項式関数を仮定しています(青線)。サンプルデータは3点だけとします(オレンジ点)。
設定関数の係数は以下の通りとしました。
w_set = [0, 2, -6, 1]
実装(正規方程式)
正規方程式は以下のように実装しました。
pp = np.dot(Phi.T, Phi)
ppi = np.linalg.inv(pp)
ppp = np.dot(ppi, Phi.T)
w_ml1 = np.dot(ppp, y_sample)
ここで、Phiは計画行列を表します。
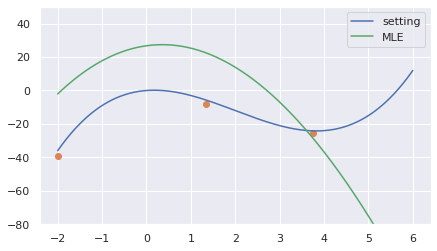
推論結果は下図の通りです。緑線が推定した関数です。
3点のデータで3次の多項式なので完全にデータ点を通って欲しいのですが全然値がずれています。
推定結果としての係数ベクトルは以下の通りとなりました。
[26.74957281 3.67629247 -5.20741295 0.08003123]
実装(擬似逆行列)
擬似逆行列を使った場合は以下の通りです。
pim = np.linalg.pinv(Phi)
w_ml2 = np.dot(pim, y_sample)
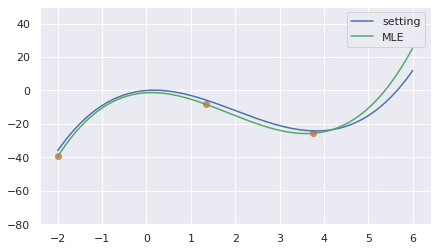
推論結果はこうなりました。
こっちは期待通り、サンプルデータを全て通る関数が推定されました。
係数ベクトルはこうなりました。
[-1.36044521 1.46444715 -6.47618665 1.16327901]
正規方程式を素直に書いた場合と値が全然違っています。
どこが悪さをしているのか?
正規方程式における逆行列の計算がまずそうです。
> np.allclose(np.dot(pp, ppi), np.eye(pp.shape[0]))
False
いくつか試してみていたところ、データ数よりもモデルの次数の方が大きい場合にこのような問題が発生しそうです。
線形モデルもライブラリに実装されているはずなので、実用上はあまり問題にならないと思います。
ですが、線形回帰は学習用によく使われているとも思うので、同じような問題にぶつかる方もいるのかなと思って書きました。
実装
実装したnotebookは以下のリンクで確認してください。
そして、何か問題を見つけていただけたら優しく教えていただけると泣いて喜びます。