決定性有限オートマトンの状態最小化アルゴリズム (Moore's algorithm)

決定性有限オートマトン(Deterministic Finite Automaton: DFA)という種類のオートマトンについて、最小の状態数を持つ等価なオートマトンを得ることを**DFA最小化(DFA minimization)**という。
この記事では、DFA最小化を行うアルゴリズムの一つであるMoore's algorithmの解説と、C++での実装例を示す。

Deterministic Finite Automaton とは

（有限）オートマトンは大きく分けると「認識機械（acceptor, recognizer）」と「順序機械（transducer）」の２種類に大きく分類される。acceptorは入力の文字列を受け取った結果としてaccept/rejectの二値を返すもの、transducerは出力の文字列を返すものである。
acceptorはさらにDeterminisitc Finite Automaton (DFA), Non-determinisitc Finite Automaton (NFA), epsilon-NFA などに分類できるが、相互に変換できることも知られている。また、transducerもMoore machine, Mealy machineの二つに分類できるが、この二つも相互に変換できる。

この記事で扱う対象はacceptorの一つであるDFAである。

DFAは $M=(Q,\Sigma,\delta,q_0,F)$ のタプルとして定義され、下のような図で図示される。

• $Q$ は状態集合（下図の例で言えば`$\{a,b,c,d,e,f\}$）
• $\Sigma$ は文字集合(下図の例では$\{0,1\}$)
• $\delta$は遷移関数 (写像$\delta : Q \times \Sigma \to Q$、下図の例でいう状態を繋ぐ矢印)
• $q_0$は始状態($a$)
• $F$は受理状態の集合($F \subseteq Q$, 下図の例では$\{c,d,e\}$, 二重丸で囲まれた状態で表される)

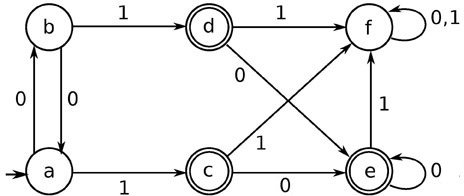
(https://en.wikipedia.org/wiki/DFA_minimization#/media/File:DFA_to_be_minimized.jpg より)

DFA minimization

DFA minimizationは、オートマトンの挙動を維持しつつオートマトンの内部状態の数を最小化することである。
「あらゆる入力文字列に対して同じ結果をもたらす２つの状態」があればそれらは「等価」であるといえ、互いに区別する必要がないための一つの状態とみなすことができる。
このような等価な状態を最小の数にまとめていくことによって最小限のオートマトンを構築することができる。このように最小化したオートマトンは一意に定まる。

上図の例について考えよう。

• 上の状態のうち、状態$\{c, d\}$ はいずれも、0の入力に対して$e$に遷移し、1の入力に対して$f$に遷移する。よってこの２つの内部状態は等価である。
• また、状態$\{c,d\}$ を一つの状態とみなすと状態$a$,$b$も等価とみなせる。(入力0によって$\{a,b\}$に遷移し、入力1によって$\{c,d\}$に遷移するため)
• さらに同様に考えることによって、状態$\{c,d\}$と$e$も等価であることがわかる。
  よって最終的な最小化されたオートマトンは下の図のようになる。

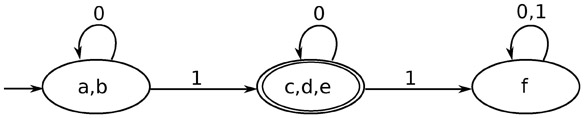
(https://en.wikipedia.org/wiki/DFA_minimization#/media/File:Minimized_DFA.jpg より)

このような最小化されたオートマトンを求めるアルゴリズムはいくつか存在する。(Hopcroft's algorithm, Moore's algorithm, Brzozowski's algorithm)
ここでは最も基本的なMoore's algorithmについて解説する。

Moore's algorithm

Moore's algorithmをざっくりというと、「まず状態を受理状態（二重丸ノード）と拒否状態（一重丸ノード）に大きく分割し、その分割をより細かく分けていくことを繰り返し、それ以上細かく分けられないところまで続ける」という手法である。

英語だが、こちらの動画はとてもわかりやすい。
解説動画 : https://youtu.be/hOzc4BUIXRk

ここで用語を定義しておく。ここではある状態のペアが n-equivalent である状態というのを、長さnの任意の文字列を受け取った時に同じ結果を返す状態と定義する。ただし、0-equivalentは、その状態自身のaccept/rejectが同じ状態であることと定義する。
DFA最小化は $|Q|$-equivalentであるような状態のセットに分割するという作業に他ならない。
$i$-equivalentは、$(i-1)$-equivalentかどうかがわかっていれば判定しやすい。なぜなら、ある状態$n_i$,$n_j$が、任意の一文字の入力を受け取った時に到達した先が$(i-1)$-equivalentならば、それ以後任意の$(i-1)$個の入力を受け取った時に到達する結果が同じということを意味し、すなわち$i$-equivalentであると判断できるからである。

このアルゴリズムでは0-equivalent, 1-equivalent, 2-equivalent, ...という分割を順次作っていく方法である。
本来ならば$|Q|$回（状態数の数だけ）実行する必要があるが、
以下の疑似コードのようなアルゴリズムで構築できる。

p_i = Q.group_by {|q| F.include?(q) }           # p_0 = [ [a,b,f], [c,d,e] ]  0-equivalentかどうかで分割する
i = 0
while true
  p_next = [ [a],[b],[c],[d],[e],[f] ]          # p_i から p_{i+1} (=p_next) を求める
  p_i.each do |g|
    for_each_pairs_in(g) do |ni, nj|            # g におけるノードペア(ni,nj)について
      if equivalent(ni, nj, p_i)                # niとnjが i-equivalent ならば
        p_next.merge(ni, nj)                    # p_nextにおけるniとnjをマージ
  break if p_i == p_next                        # 変化がなければ、それ以上探索する必要がないので打ち切る
  p_i = p_next
  i += 1
end

C++ implementation

上記のアルゴリズムをC++で実装すると以下のようになる。
(gistはこちら)

# include <iostream>
# include <utility>
# include <vector>
# include <set>
# include <cassert>

class DFA {
  public:
  DFA(int n, int z, std::set<int> f, std::vector<std::vector<int>> _delta) :
  N(n), Z(z), F(std::move(f)), delta(std::move(_delta)) {
    // validity check
    for (int i: F) { assert(i < N); }
    assert(delta.size() == N);
    for (const auto& a: delta) {
      assert(a.size() == Z);
      for (const int i: a) { assert(i < N); }
    }
  };
  int N;  // number of internal states
  int Z;  // number of alphabets
  std::set<int> F;  // set of final states
  std::vector< std::vector<int> > delta; // state-transition function.
  // represented by NxZ two-dim vector. delta[q][s] = transition from state-q by input s
};

bool Equivalent(const DFA& dfa, int i, int j, const std::vector<int>& partition_0) {
  for (int z = 0; z < dfa.Z; z++) {  // for input z
    int dest_i = dfa.delta[i][z];
    int dest_j = dfa.delta[j][z];
    if (partition_0[dest_i] != partition_0[dest_j]) return false;
  }
  return true;
}

std::vector<int> Minimize(const DFA& dfa) {
  const int N = dfa.N;

  std::vector<int> partition_0(N, -1);
  // initialize grouping by the final state
  int accept_idx = *dfa.F.begin(), reject_idx = -1;
  for (int i: dfa.F) {
    partition_0[i] = accept_idx;
  }
  for (int i = 0; i < N; i++) {
    if (partition_0[i] < 0) {
      if (reject_idx < 0) reject_idx = i;
      partition_0[i] = reject_idx;
    }
  }

  while (true) {
    std::vector<int> partition(N, -1);
    int i = 0;
    while (i < N) {
      partition[i] = i;
      int i_next = N;
      for (int j = i+1; j < N; j++) {
        if (partition[j] >= 0) continue;  // skip if j is already merged
        if (partition_0[i] == partition_0[j] && Equivalent(dfa, i, j, partition_0)) {
          partition[j] = i;   // merge i & j
        }
        else if (i_next == N) { i_next = j; }  // keep the first unmerged node
      }
      i = i_next;
    }
    if (partition_0 == partition) break;
    partition_0 = partition;
  }

  return partition_0;
}

int main(int argc, char* argv[]) {
  DFA dfa1(6, 2, {2,3,4}, {{1,2}, {0,3}, {4,5}, {4,5}, {4,5}, {5,5}});
  auto m1 = Minimize(dfa1);
  std::vector<int> ans = { 0,0,2,2,2,5 };
  for (auto x: m1) {
    std::cerr << x << ", ";
  }
  assert(m1 == ans);

  return 0;
}

まず最初のDFAクラスは、DFAオートマトンを表すクラスである。
そのDFAのインスタンスに対して、Minimize関数を呼ぶと最小化されたクラスの分割が返される。分割はstd::vector<int>で返され、$i$番目の状態が属するグループのIDが格納されている。

分割の状態は長さNのstd::vector<int>で保持しているが、初期化時に値を-1で初期化している。std::vector<int> partition(N, -1);
-1という数字は、その状態がまだどのグループにも属していないという意味で使っている。