graph-toolを使ってSBM
参考:
SBMとは
Stochastic Block Model とはネットワークを確率的に生成するモデルの1つ。「ノードがいくつかの集合(ブロック)に分類され、そのブロック$r$内のノード$i$から別のブロック$s$のノード$j$にリンクを持つ確率は、$r$と$s$に依存して決まる」ということを仮定しているモデル。
つまり、あるノードがどのノードとつながりやすいかというのは所属するブロックにのみ依存する。
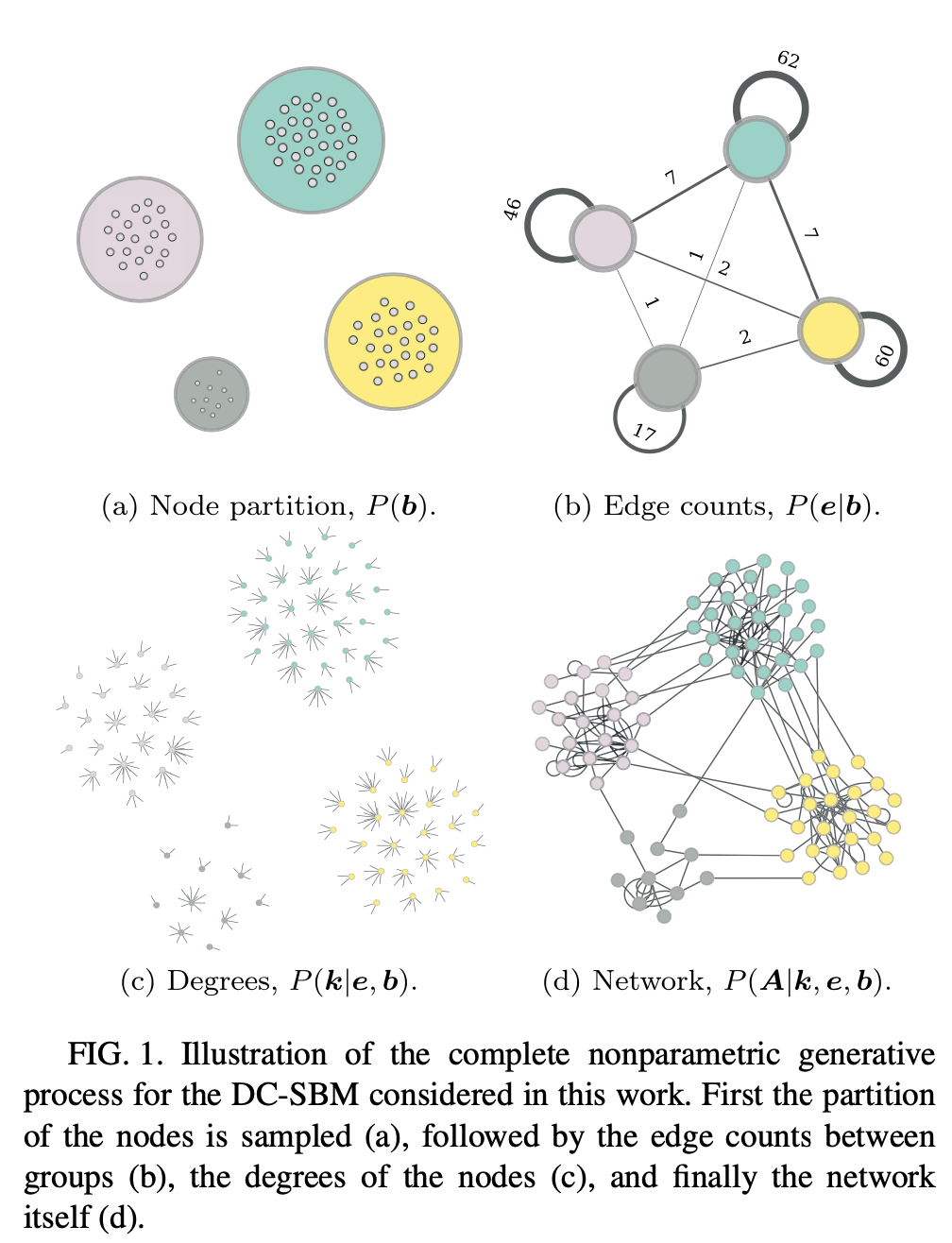
ノード$i$の所属するブロック$b_i$ を決めて、またブロックのペア$(r,s)$がリンクを持つ本数 $e_{rs}$ を指定するとネットワークが確率的に構築される。
つまりこのモデルのパラメータは $\mathbf{\theta} = \{ e_{rs} \}$ と $\mathbf{b} = \{b_i \}$ と書くことができる。
ブロック数が一つの特殊な場合としてErdos-Renyiランダムグラフを含むモデルである。
非常にシンプルなモデルなので、ある隣接行列 $A$を持つグラフが与えられたときに、それがパラメータ $(\mathbf{\theta}, \mathbf{b})$のSBMから生成される条件付き確率(尤度)を解析的に閉じた形で計算できる。
P(A | \theta, \mathbf{b})
これを使うと、ある$A$が与えられたときにブロック分割 $\mathbf{b}$の事後分布を求めることができる。
P( \mathbf{b} | A ) = \frac{ \sum_{\theta} P(A| \theta, \mathbf{b}) P(\theta, \mathbf{b}) }{ P(A) }
ここで $P(A) = \sum_{\theta, \mathbf{b}} P(A|\theta,\mathbf{b}) P(\theta, \mathbf{b})$ である。
以上は最も基本的なタイプのSBMだが、ブロック間にリンクを作る"確率"ではなく、"本数"をパラメータとして指定するようなタイプのSBMだと(microcanonical ensemble)、$A$と矛盾しない$\theta$は一通りしか存在しなくなる。そうすると上記の式はさらに簡略化され、
P( \mathbf{b} | A ) = \frac{ P(A| \theta, \mathbf{b}) P(\theta, \mathbf{b}) }{ P(A) }
つまり上記の尤度を最大化する問題(あるいは事後分布からサンプリングする問題)としてグラフのブロック分割問題を定式化できる。
degree-corrected SBM (DCSBM)
通常のSBMで生成されるネットワークの次数分布はPoisson分布(の重ね合わせ)になる。
一方で世の中の複雑ネットワークの多くはべき分布の次数分布を持つことが多いため、通常のSBMはこうしたネットワークを記述するのには適さない。
そこで各ノードの次数は制約としていれてしまうモデル $\{ k_i \}$ も考えられている。
configuration model のSBMバージョンと思えば良い。次数列もパラメータとなるため、通常のSBMよりは複雑なモデルで $\{ \mathbf{k}, \mathbf{b}, \theta \}$ がモデルのパラメータとなる。
nested stochastic block model
SBMにはdetectability limitが存在し、巨大なネットワークになると細かいブロック構造が原理的に推定できなくなる。[Tiago P. Peixoto, “Parsimonious module inference in large networks”, Phys. Rev. Lett. 110, 148701 (2013).]
細かい部分では確率的な揺らぎをシステマティックな構造から区別できなくなるため。つまり構造があるはずなのに検出できないという問題が起きてくる。
この問題を解決するために提案された手法の一つがnested stochastic block model という階層的なSBMである。(Peixoto PRX 2014)
まず最下層(layer 0と呼ぶ)では、通常のSBMのようにノードをブロックに分割する。そのlayer 0でのblock自体を一つノードとしてlayer 1のノードとしてネットワークを構築する。
このときエッジの本数は維持され、layer 1より上ではmultigraphになる。上記の階層構造を繰り返していく。
このとき、階層の深さもnonparametricに推定する方法を提案している。
これを行うことによりunderfitの問題を解決してより細かい構造をみられるようになるだけでなく、階層的なブロック構造はデータの解釈にも役に立つ。上の階層でノードを大きな分類で分割し、より細かい構造は下層の分類でみられるようになる。
モデル選択
SBMのブロック数$B$自体もnon-parametric にデータから推定する方法も提案されている。
$B$が任意の数で良いのであれば、$B$をノード数まで増やしたモデルが常に尤度最大になるが、これは明らかにoverfitしている。
ではどのように$B$(あるいはモデル自体)を選択すれば良いだろうか?
一つの方法がminimum description length (MDL) principle である。
これは「観測されたネットワーク$A$を記述するために必要な(情報論的な)情報量」を最小化するという原理である。
モデルを何を仮定しなければ$A$を明示的に$N^2$-bit で記述すればネットワークの情報を記述できる。しかしネットワークがブロック構造を持っていることがわかれば、その情報をうまく使うことで必要な情報量を少なくすることができる。
description lengthは以下のように書くことができ、
\Sigma = - \ln P(A | \mathbf{b}, \theta) - \ln P(\mathbf{b}, \theta)
第1項は対数尤度、第2項はモデルを定義の複雑さに対応する。
あるモデルを決めれば、second termは一定なので、最尤推定することは$\Sigma$を最小化することに対応する。
複雑さの異なる2つのモデルを比較する際は、2つのモデルでそれぞれ尤度を最大化して、そのときの尤度を用いてdescription lengthを評価し、description lengthが小さい方のモデルを採用する。
つまり、モデルのfitの良さと複雑さのトレードオフの関係を表した式になっており、$\Sigma$の小さいモデルを選択することによって、同じくらいフィットが良いモデルが会った際によりシンプルなモデルを選択することができる。(オッカムの剃刀)
weighted graph
上記のフレームワークを重み付きのネットワークに拡張する。
[Tiago P. Peixoto, “Nonparametric weighted stochastic block models”, Phys. Rev. E 97, 012306 (2018)]
重み付きグラフは隣接行列 $A = \{A_{ij}\}$ に加えて、各リンクの重み discrete or real edge covariates $\mathbf{x} = \{ x_{ij} \}$ によって表されている。
さらに、エッジが存在するかどうかは重みと関連していないと仮定する。つまり、「エッジが存在しない」という事象は「重み0のエッジが存在する」という事象とは異なる。
ここでは以下のようなSBMを考える
- ノードが$B$のグループ $b_i \in \{1 \dots B \}$ に属する
- エッジの配置だけでなく、重みも両端のブロックからサンプルされる
つまり、エッジの配置も重みもそれぞれブロックの所属情報にのみ依存してサンプルされるということ。重みの分布を特徴付けるパラメータを$\gamma$とすると
P( A, \mathbf{x} | \theta, \gamma, \mathbf{b}) = P(x | A, \gamma, \mathbf{b}) P(A | \theta, \mathbf{b})
ただし、covariate $x$ は存在するエッジにのみサンプルされる。
P( \mathbf{x} | A, \gamma, \mathbf{b} ) = \prod_{r \leq s} P( \mathbf{x}_{rs} | \gamma_{rs} )
where $\gamma_{rs}$ is a set of parameters that govern the sampling of the weights between blocks $r$ and $s$.
graph-tool でのブロックの推定方法
では実際にgraph-toolでどのようにブロック推定をすればよいのかという方法について解説する。
以下では前提条件として次のモジュールをインポートした状態であるとし、またサンプルデータとしてC.Elegansの神経系のデータを利用する。
import graph_tool.all as gt
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
g = gt.collection.data["celegansneural"]
最小限の実行方法
基本的にnested block modelの方がより詳細にブロック構造を推定することができるため、以下では基本的にnested SBMを使った推定について解説する。
単純に推定するだけであれば非常に簡単である。minimize_nested_blockmodel_dl を呼ぶだけ。
state = gt.minimize_nested_blockmodel_dl(g)
Degree-corrected SBM (DCSBM)を使って推定したい場合はdeg_corrをパラメータとして渡す。
state = gt.minimize_nested_blockmodel_dl(g, deg_corr = True)
返り値としてNestedBlockStateのインスタンスが返る。drawメソッドを呼ぶと階層的なブロック構造をかっこよく描画してくれる。
state.draw()
fitした状態のdescription length を求めるには次のようにする。
state.entropy() # => 8251.84
当然ながら最適なblockはMonte Carloで推定しているので実行するたびに結果は多少揺れる。何回か実行して結果が安定していることを確認する方がよいだろう。
(最尤推定だけでなく、事後分布からサンプリングする方法も提供されている。詳しくはドキュメント を参照していただきたい。)
各ノードのブロックのラベルを得たい場合は get_bsメソッドを呼ぶ。
state.get_bs()
# =>
[PropertyArray([ 0, 0, 1, 1, 1, 0, 2, 0, 3, 3, 4, 0, 1, 2, 0,
5, 0, 5, 5, 5, 5, 5, 5, 6, 6, 6, 5, 5, 4, 5,
5, 5, 5, 5, 6, 6, 6, 6, 5, 0, 5, 5, 7, 6, 8,
5, 6, 6, 6, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 3, 6, 0, 5, 3, 5, 5, 5, 5, 3, 6, 6,
6, 5, 6, 6, 6, 6, 6, 5, 5, 1, 3, 1, 3, 6, 3,
3, 5, 0, 7, 6, 3, 9, 9, 10, 0, 0, 0, 0, 0, 3,
0, 3, 4, 0, 0, 0, 10, 3, 4, 0, 4, 0, 1, 1, 10,
0, 0, 4, 10, 4, 1, 4, 4, 4, 0, 3, 3, 3, 8, 4,
4, 4, 7, 4, 4, 4, 4, 8, 4, 4, 10, 4, 4, 10, 10,
4, 11, 9, 9, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11,
9, 9, 9, 11, 11, 12, 13, 1, 11, 12, 9, 9, 9, 11, 11,
11, 11, 11, 9, 12, 13, 12, 1, 11, 14, 7, 8, 11, 7, 12,
7, 11, 14, 10, 10, 14, 0, 10, 10, 10, 10, 7, 10, 4, 6,
3, 3, 3, 13, 3, 10, 3, 13, 13, 14, 12, 9, 3, 3, 0,
3, 12, 9, 12, 12, 11, 14, 11, 14, 14, 3, 3, 14, 14, 3,
5, 3, 6, 6, 10, 14, 9, 12, 12, 9, 9, 9, 12, 9, 9,
12, 12, 12, 12, 12, 6, 13, 11, 11, 11, 11, 11, 11, 9, 14,
14, 14, 14, 9, 9, 14, 14, 9, 9, 14, 9, 9, 14, 10, 9,
6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6],
dtype=int32),
PropertyArray([0, 1, 2, 0, 0, 0, 2, 3, 3, 4, 3, 4, 4, 2, 4], dtype=int32),
PropertyArray([0, 0, 0, 0, 0], dtype=int32)]
例えば、ノード$i$のブロックは state.get_bs()[0][i] で取得できる。
重み付きネットワークのブロック推定
先ほどと同様にminimize_nested_blockmodel_dlメソッドを使えば良いが、オプション引数として以下のように指定する。
state = gt.minimize_nested_blockmodel_dl(g, state_args=dict(recs=[g.ep.value],
rec_types=["real-normal"]))
ここでは、エッジの重みがg.ep.valueのEdgePropertyとして格納されているため、それをrecsのパラメータとして指定する。
また、フィットする分布としてここでは正規分布を指定している。他に利用可能な値は "real-exponential", "discrete-geometric", "discrete-binomial", "discrete-poisson" がある。
また重みだけでなく他のエッジの属性も同様にフィッティングすることができ、複数の属性を指定することもできる。
どの分布がよいモデルになっているのかの評価は、やはりminimum description length principleに基づいて行えばよい。つまり、state.entropyが最小になるものを選択する。
重みが幅広い分布の場合、例えばlog-normalでフィットしたい場合は重みをlogで変数変換して"real-normal"でフィッティングすればよい。
y = g.ep.value.copy()
y.a = log(y.a)
state = gt.minimize_nested_blockmodel_dl(g, state_args=dict(recs=[y], rec_types=["real-normal"]))
ただし、変数変換の分も考慮に入れたdescription length(を負符号にしたもの)は以下のようになる。複数のモデルを比較する場合、この値が小さい方を選ぶ。
state.entropy() + log(g.ep.value.a).sum()
Merge-Split Monte Carlo法で最適化を改善する
blockの推定にはMCを使うので、必ずしも最適な状態を得られているとは限らないし、実際ほとんどの場合局所最適になっているだろう。
それでも実用上十分によく推定できていると思われるが、さらに改善したい場合はMerge-Split MCMCのアルゴリズムを使って最適化をすると、もう少し改善した結果が得られることが多い。
state = gt.minimize_nested_blockmodel_dl(g, state_args=dict(recs=[g.ep.value], rec_types=["real-normal"]))
# improve solution with merge-split
state = state.copy(bs=state.get_bs() + [np.zeros(1)] * 4, sampling=True)
for i in range(100):
ret = state.multiflip_mcmc_sweep(niter=10, beta=np.inf)
上のようにすることでMerge-Split MCMCを使って解を改善することができる。
最初にstate.copyしている箇所では、ネストが深くなったり浅くなったりすることも許容するために、事前にblock数1でネストを深くしている。
これで分割を推定することはできるのだが、ここで得られた状態を描画すると以下のようになり、冗長なネストが残ったままになっていることがわかる。
そこで、以下のように冗長なネストを削除する。
# minimize level
def minimize_state_nest(state):
i = 0
while True:
ls = state.get_levels()
if i + 2 >= len(ls): # keep the top-most level
break
if ls[i].get_nonempty_B() == ls[i+1].get_nonempty_B():
state.delete_level(i+1)
else:
i += 1
minimize_state_nest(state)
すると、以下のように中間の冗長なレベルの分割を取り除くことができる。
この冗長なネストが残る問題は重みつきネットワークの場合のみ起きるようだ。
重みつきグラフのブロック状態の描画
重みにもとづいてエッジの色や太さを変えて描画するには以下のようにする。
state.draw(
edge_color=gt.prop_to_size(g.ep.value, power=1, log=True),
ecmap=(matplotlib.cm.inferno, .6),
eorder=g.ep.value,
edge_pen_width=gt.prop_to_size(g.ep.value, 1, 4, power=1, log=True),
edge_gradient=[])
他にもグラフ描画のメソッドgt.drawと同じように引数を渡すことができる。
ノードの名前を描画する
これらのように円形に配置したあとでノードの名前を描画するには以下のようにする。
def draw_nested_with_node_names(state):
b = state.g.new_vertex_property("int")
b.a = state.get_bs()[0]
pos,t,t_pos = state.draw(vertex_text = b, vertex_text_position=0,vertex_font_size = 12)
x_pos = [pos[v][0] for v in g.vertices()]
y_pos = [pos[v][1] for v in g.vertices()]
angle = g.new_vertex_property("double")
angle.a = np.arctan2(y_pos,x_pos)
state.draw(
pos=pos,
edge_color=gt.prop_to_size(g.ep.weight, power=1, log=True),
ecmap=(matplotlib.cm.inferno, .6),
eorder=g.ep.weight, edge_pen_width=gt.prop_to_size(g.ep.weight, 1, 4, power=1, log=True),
edge_gradient=[],
vertex_text = g.vp.name,
vertex_text_position=0,
vertex_text_offset=[0,0],
vertex_font_size=20,
vertex_text_rotation = angle,
output_size=(2000,2000))
return pos,t,t_pos
pos,t,t_pos = draw_nested_with_node_names(state)
このように放射状に名前を表示するには、state.drawを2回呼ぶ必要がある。
1回目は放射状に配置して、その戻り値pos にノードの位置情報が入っている。その情報を使って文字の角度を計算し、vertex_text_rotationのパラメータで文字の角度を指定している。
ブロック間のリンク数を計算する
分割したブロックの意味合いを解釈するために、ブロック間で実際に何本程度のリンクが貼られているのかを計算する。
def calc_eij_wij(g, bs0, weight):
B = int(bs0.max()) + 1
eij = np.zeros((B,B))
wij = np.zeros((B,B))
for ni in g.vertices():
for e in ni.out_edges():
nj = e.target()
i = g.vertex_index[ni]
j = g.vertex_index[nj]
bi = bs0[i]
bj = bs0[j]
eij[bi][bj] += 1
wij[bi][bj] += weight[e]
wij_avg = np.divide(wij, eij, out=np.zeros_like(wij), where=eij!=0)
return eij, wij, wij_avg
bs0 = state.get_bs()[0] # the lowest-level partition
eij,wij,wij_avg = calc_eij_wij(g, bs0, g.ep.value)
eij,wij,wij_avg
eij がblock $i$-$j$間のリンクの本数の総和、wijが重みの総和、wij_avgが1本のエッジあたりの重みの平均値。
エッジが存在しない場合に0割りが発生しないようにnp.divideを使って計算している。
描画する際には plt.matshow を使うと手軽に描画できる。
plt.matshow(eij_null)
plt.colorbar()
平均重みをlog-scaleでプロットする
plt.matshow(np.log(wij_avg))
plt.colorbar()
また、Degree-Corrected SBMを使用した場合は、対応するconfigurationモデルと比較したくなるだろう。以下のようにすると対応する次数を維持したnull modelと比較できる。
def calc_eij_null(g, bs0):
B = int(bs0.max()) + 1
out_deg_sum = [0] * B
in_deg_sum = [0] * B
for i,v in enumerate(g.vertices()):
bi = bs0[i]
in_deg_sum[bi] += v.in_degree()
out_deg_sum[bi] += v.out_degree()
null_ij = np.zeros((B,B)) # initialize BxB matrix
E = sum(in_deg_sum)
for i in range(B):
for j in range(B):
null_ij[i][j] = out_deg_sum[i] * in_deg_sum[j] / E
return null_ij
eij_null = calc_eij_null(g, bs0) # calculation of the null model
def plot_diff(eij, eij_null):
dij = np.divide( eij - eij_null, np.sqrt(eij_null), out=np.zeros_like(eij), where=eij_null!=0)
scale = max( abs(dij.max()), abs(dij.min()))
plt.matshow(dij, vmin = -scale, vmax = scale, cmap = matplotlib.cm.RdBu)
plt.colorbar()
plot_diff(eij, eij_null)