SpatiaLiteで再帰クエリを使ってポリゴンを半分に分割してみた

今年も FOSS4G Advent Calendar 2016 に参加します！

こんにちは。昨年に引き続いて、SpatiaLiteでがんばることにしました。
（´-`）.｡oO（あとでその2にも何か（どうでもいいものを）書きたいな

さて、今日のネタは、再帰クエリを使ってポリゴンを半分に分割してみたというお話。

最近、ベクタデータの作業は何でもかんでもSpatiaLiteに頼りっぱなしなのですが、そんなある日、
「このエリアのポリゴンが全体的に大きすぎるから、とりあえず半分に分割できない？」
というご依頼をいただきました。

聞けば、面積が等分になるなら、東西でも南北でもなんでもよいらしく、とにかく半分に
してちょうだい、ということでした。

「きっとPythonか何かでスクリプト書いて、ループを使って切断する線の位置を少しずつ
ずらしながら、半分になる位置を探せばできるかなー？」と思ったのですが、
そこをあえてSQLだけでできないかしらと、挑戦してみました。

ニッチなネタで需要は全然ないような気もしますが笑、やってみたネタとして投稿します。

ポリゴンの分割（SpatiaLite）

ポリゴンを分割する、またはポリゴンの一部を抽出するには、

• Split（ST_Split）を使う
• SplitRight（ST_SplitRight） or SplitLeft（ST_SplitLeft）を使う
• Intersection（ST_Intersection）を使う

などの方法があります。

Split（ジオメトリを他のジオメトリによって分割する）

名前の通り、あるジオメトリ geom_0 を、切断に使用するジオメトリ geom_blade で切断するものです。

Split( -- ST_Split も可
    geom_0, geom_blade
)

切断後に複数の地物になる場合は、マルチポリゴンなどのマルチジオメトリになります。

SplitRight（Splitで切断されたジオメトリの一部分を返す）

SplitRight( -- ST_SplitRight も可
    geom_0, geom_blade
)

この空間関数は、常にシングルポリゴンなどのシングルジオメトリが返ります。
切断によって片側に複数のジオメトリが生成される場合にも、そのうちの一つだけが選択されるため、注意が必要です。

さらに、名前にはRightとありますが、そもそも何をもって右なのか、よくわかりません^^;
仮にノースアップにした際の右側だとしても、 geom_0 と geom_blade の組み合わせによって結果が右側だったり左側だったりするようです。

SplitLeft（Splitで切断されたジオメトリの左側を除外したジオメトリを生成する）

SplitLeft( -- ST_SplitLeft も可
    geom_0, geom_blade
)

SplitRightの対をなすような空間関数です。
ただし、SplitLeftはSplitRightで選択された残りのすべてが返るため、
SplitRightと違って、場合によっては結果がマルチジオメトリで返ります。

Intersection（二つのジオメトリの交差を返す）

Intersection( -- ST_Intersection も可
    geom_1, geom_2
)

複数のジオメトリの交差を返すIntersectionは、ジオメトリの一部を抽出する機能として
利用することもできます。

いろいろ試してみた結果 Intersectionを利用するのが一番シンプルでよさそう という
ことになったので、ここではそのクエリを紹介します。

まず、ざっくり分割してみる

ということで、とあるポリゴンAを持ってきました。（去年の記事のとおなじものです^^;）

SELECT
    GeomFromText(
        'POLYGON((
            139.72798347473145 35.743795434320500,
            139.71708297729492 35.733763275056724,
            139.72987174987793 35.725889931646370,
            139.73201751708984 35.721569713458500,
            139.73459243774414 35.721569713458500,
            139.74343299865723 35.728398337919580,
            139.73648071289062 35.735226377009106,
            139.72798347473145 35.743795434320500
        ))', 4612
) AS geom_0 -- ポリゴンAの形状
;

こんなの。

これを、「東半分と西半分に切断」したいと思います。

まず、ジオメトリを包含する長方形ポリゴン（SpatiaLiteでは、MBRと呼びます）を生成して、その半分に含まれるポリゴンの部分を抽出します。
*MBR：Minimum Bounding Rectangle

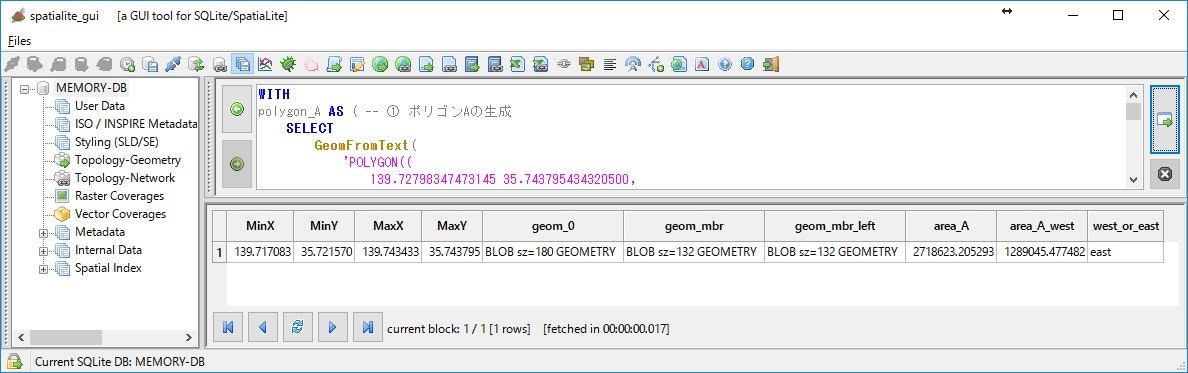
まず、ポリゴンのMBRと、その西側半分の長方形を生成してみます。

MBRの生成

WITH
polygon_A AS ( -- ① ポリゴンAの生成
    SELECT
        GeomFromText(
            'POLYGON((
                139.72798347473145 35.743795434320500,
                139.71708297729492 35.733763275056724,
                139.72987174987793 35.725889931646370,
                139.73201751708984 35.721569713458500,
                139.73459243774414 35.721569713458500,
                139.74343299865723 35.728398337919580,
                139.73648071289062 35.735226377009106,
                139.72798347473145 35.743795434320500
            ))', 4612
    ) AS "geom_0" -- ポリゴンAの形状
),
select_mbr_coord AS ( -- ② ポリゴンAのMBRの端点座標を得る
    SELECT
        MbrMinX("geom_0") AS "MinX",
        MbrMinY("geom_0") AS "MinY",
        MbrMaxX("geom_0") AS "MaxX",
        MbrMaxY("geom_0") AS "MaxY",
        "geom_0"
    FROM polygon_A
)
SELECT
    *,
    BuildMbr("MinX","MinY","MaxX","MaxY") AS "geom_mbr",
    BuildMbr("MinX","MinY","MinX"+("MaxX"-"MinX")/2,"MaxY") AS "geom_mbr_left"
FROM select_mbr_coord
;

上記のSQLについて、簡単に解説します。

• まず、はじめにポリゴンAを生成し、 geom_0 と名前をつけます。（コメント①の部分： サブクエリ polygon_A）

• 次に、ポリゴンAの端点座標をそれぞれ MinX, MinY, MaxX, MaxY というそのままな関数で取得します。（②の部分： select_mbr_coord）

• これをもとに、geom_0 を包含する長方形と、さらに西側半分の長方形を生成します。
  BuildMbr というのが、長方形を生成する空間関数です。これに端点座標を与えるのですが、西側半分の長方形はX座標の最大値が MinXとMaxXの中間になるので、 "MinX"+("MaxX"-"MinX")/2 という形に置き換わっています。
  （実は、ジオメトリを包含する長方形を直接取得する Extent という空間関数もあるのですが、こちらは「集計関数」として機能するため、複数のジオメトリをまとめて処理する場合、ジオメトリ全体を包含する長方形を生成してしまいます。）

なお、X方向の領域の中点を得る "MinX"+("MaxX"-"MinX")/2 は ("MaxX"+"MinX")/2 と整理できるので、以下はそのように表記します。

さて、それでは、西側半分の長方形でポリゴンAの西側部分を抽出して、面積を比べてみましょう。

WITH
polygon_A AS ( -- ① ポリゴンAの生成
    SELECT
        GeomFromText(
            'POLYGON((
                139.72798347473145 35.743795434320500,
                139.71708297729492 35.733763275056724,
                139.72987174987793 35.725889931646370,
                139.73201751708984 35.721569713458500,
                139.73459243774414 35.721569713458500,
                139.74343299865723 35.728398337919580,
                139.73648071289062 35.735226377009106,
                139.72798347473145 35.743795434320500
            ))', 4612
    ) AS "geom_0" -- ポリゴンAの形状
),
select_mbr_coord AS ( -- ② ポリゴンAのMBRの端点座標を得る
    SELECT
        MbrMinX("geom_0") AS "MinX",
        MbrMinY("geom_0") AS "MinY",
        MbrMaxX("geom_0") AS "MaxX",
        MbrMaxY("geom_0") AS "MaxY",
        "geom_0"
    FROM polygon_A
),
build_mbrs AS (
    SELECT
        *,
        BuildMbr("MinX","MinY","MaxX","MaxY") AS "geom_mbr",
        BuildMbr("MinX","MinY",("MaxX"+"MinX")/2,"MaxY") AS "geom_mbr_left"
    FROM select_mbr_coord
) -- ここまでほぼ同じ
SELECT
    *,
    ST_Area("geom_0",1) AS "area_A", -- ポリゴンAの面積
    ST_Area(ST_Intersection("geom_0","geom_mbr_left"),1) "area_A_west", -- MBRの西側半分で抽出したポリゴンAの部分の面積
    CASE -- 半分に分割する本来の位置はどちら側にあるか？
        WHEN ST_Area(ST_Intersection("geom_0","geom_mbr_left"),1) > ST_Area("geom_0",1)/2 THEN 'west'
        WHEN ST_Area(ST_Intersection("geom_0","geom_mbr_left"),1) < ST_Area("geom_0",1)/2 THEN 'east'
        WHEN ST_Area(ST_Intersection("geom_0","geom_mbr_left"),1) = ST_Area("geom_0",1)/2 THEN 'half'
        ELSE 'unknown'
    END AS "west_or_east"
from build_mbrs
;

上記の最後のSELECT文の説明です。
（前述のクエリ（MBRの生成）の最後のSELECT文の部分を build_mbrs としてサブクエリに変更した他は、WITH構文内はほぼ同じです。）

• ST_Area は、ジオメトリの面積を得る関数です。二番目の引数（＝1）は、曲面近似で面積を算出するオプションです。（緯度経度の場合のみ指定可能）
• ST_Intersection は上述のとおり交差を得る関数なので、西半分のMBRでポリゴンAの部分を抽出していることになります。
• 最後の case-end 文は、「面積を2分割するxの位置は西と東のどちらにあるか？」を判定しています。もしポリゴンAをMBRの西側半分で抽出した部分の面積がポリゴンAの面積の1/2よりも大きければ、ポリゴンAを等分する正しいxはMBRの中点より西側にある（＝MBRの中点よりもさらに西にスライドする必要がある）ということになります。

クエリの実行結果は以下のようになります。

west_or_east の判定は east でした。すなわち、geom_0のMBRを2等分するラインより東側に、本来の等分線があるということになります。

さて、上のクエリでは、半分にしたMBRでポリゴンの一部を抽出し、面積を比較するとどうなるか、という処理を実行しました。
このMBRの分割処理を繰り返し行うことによって、そのうちほんとうの等分割位置にたどり着けるだろう、という発想です。

そこで、再帰クエリを利用してみることにします。

再帰クエリで等分割線を探す

再帰クエリ？

再帰クエリ (英: recursive query) もしくは 階層クエリ (英: hierarchical query) は、再帰的な問い合わせを行う SELECT ステートメントである。階層構造を持つデータなどに使う。
再帰クエリ - Wikipedia

再帰クエリ（再帰問い合わせ）とは、SELECT文によって取得した結果をさらに同じSELECT文に入力（自己参照）することで、再帰的に結果を取得するというものです。

SpatiaLiteのベースになっているSQLiteでも、再帰クエリが利用できます。
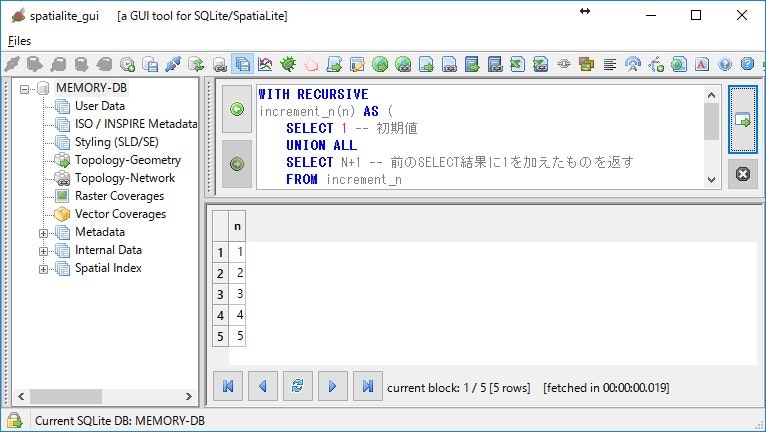
以下に例を示します。

再帰クエリによる連番生成

WITH RECURSIVE
increment_n(n) AS (
    SELECT 1 -- 初期値
    UNION ALL
    SELECT n+1 -- 前のSELECT結果に1を加えたものを返す
    FROM increment_n
)
SELECT n
FROM increment_n
LIMIT 5
;

WITH構文内で生成されている increment_n という名前の部分が再帰問い合わせになっています。
1. SELECT 1 の部分で初期値を与え、さらにこの結果に increment_n を自己参照した選択結果を縦方向に結合（UNION ALL）しています。
2. そして、その結果を、最後のSELECT文で取得しています。
なお、その際にLIMIT句で制限を指定しないと、再帰問い合わせが無限ループとなり、クエリが終わりません。

なお、再帰クエリはWITH構文内でしか使用できません。また、複数のサブクエリにまたがった再帰は行えないため、注意が必要です。
ちなみに、上記ではWITH RECURSIVEと明示していますが、実はRECURSIVEがなくても何ら問題はありません。

ポリゴンAの分割

上述のMBRでの分割では、一回のみの処理でしたが、

1. ポリゴンをMBRの半分で分割する
2. 分割した結果で面積を比較し、どちら側に本来の等分位置が含まれるかを取得する
3. 本来の等分位置が含まれる側の長方形（＝最初のMBRの半分）を新たに生成する（端点座標を取得する）
4. 3で取得した長方形を再参照し、この長方形を半分に分割する位置でポリゴンを再度分割する
5. 2へ戻り、再度面積を比較し、本来の等分位置を判定する（以下繰り返し）

という処理を行って、有限回の繰り返しで等分位置を取得してみました。

ポリゴンAの分割

WITH RECURSIVE
polygon_A AS ( -- ① ポリゴンAの生成
    SELECT
        GeomFromText(
            'POLYGON((
                139.72798347473145 35.743795434320500,
                139.71708297729492 35.733763275056724,
                139.72987174987793 35.725889931646370,
                139.73201751708984 35.721569713458500,
                139.73459243774414 35.721569713458500,
                139.74343299865723 35.728398337919580,
                139.73648071289062 35.735226377009106,
                139.72798347473145 35.743795434320500
            ))', 4612
    ) AS "geom_0" -- ポリゴンAの形状
),
select_mbr_coord AS ( -- ② ポリゴンAのMBRの端点座標を得る
    SELECT
        MbrMinX("geom_0") AS "MinX",
        MbrMinY("geom_0") AS "MinY",
        MbrMaxX("geom_0") AS "MaxX",
        MbrMaxY("geom_0") AS "MaxY",
        "geom_0",
        ST_Area("geom_0",1) AS "area_A" -- ポリゴンAの面積を追加
    FROM polygon_A
),
recursive_split AS (
    -- まず一回目の選択
    SELECT
        1 AS "level",
        "MinX" AS "MinX_0", -- ポリゴンAのMBRのMinX（＝西側の端点）
        CASE -- 半分に分割する本来の位置はどちら側にあるか？
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX","MinY",("MaxX"+"MinX")/2,"MaxY")),1) >= "area_A"/2 -- 西側にある場合
                THEN "MinX" -- 次のMBRの最小側（西端）は据え置き
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX","MinY",("MaxX"+"MinX")/2,"MaxY")),1) <  "area_A"/2 -- 東側にある場合
                THEN ("MaxX"+"MinX")/2 -- 次のMBRの最小値（西端）を現在のMBRの中点まで（＝東側へ）シフトする
        END AS "MinX",
        "MinY",
        CASE -- 半分に分割する本来の位置はどちら側にあるか？
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX","MinY",("MaxX"+"MinX")/2,"MaxY")),1) >= "area_A"/2 -- 西側にある場合
                THEN ("MaxX"+"MinX")/2 -- 次のMBRの最大値（東端）を現在のMBRの中点まで（＝西側へ）シフトする
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX","MinY",("MaxX"+"MinX")/2,"MaxY")),1) <  "area_A"/2 -- 東側にある場合
                THEN "MaxX" -- 次のMBRの最大側（東端）は据え置き
        END AS "MaxX",
        "MaxY",
        "geom_0", -- ポリゴンA
        "area_A", -- ポリゴンAの面積
        ST_Area(ST_Intersection("geom_0",BuildMbr("MinX","MinY",("MaxX"+"MinX")/2,"MaxY")),1) AS "area_A_west", -- 西側半分で抽出したポリゴンAの部分の面積
        CASE -- 半分に分割する本来の位置はどちら側にあるか？
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX","MinY",("MaxX"+"MinX")/2,"MaxY")),1) > "area_A"/2 THEN 'west'
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX","MinY",("MaxX"+"MinX")/2,"MaxY")),1) < "area_A"/2 THEN 'east'
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX","MinY",("MaxX"+"MinX")/2,"MaxY")),1) = "area_A"/2 THEN 'half'
            ELSE 'unknown'
        END AS "west_or_east"
    FROM select_mbr_coord
    -- ここまでが一回目の選択

    UNION ALL

    -- ここからが二回目以降の再帰的な選択
    SELECT
        "level"+1,
        "MinX_0",
        CASE -- 半分に分割する本来の位置はどちら側にあるか？
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX_0","MinY",("MaxX"+"MinX")/2,"MaxY")),1) >= "area_A"/2 -- 西側にある場合
                THEN "MinX" -- 次のMBRの最小側（西端）は据え置き
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX_0","MinY",("MaxX"+"MinX")/2,"MaxY")),1) <  "area_A"/2 -- 東側にある場合
                THEN ("MaxX"+"MinX")/2 -- 次のMBRの最小値（西端）を現在のMBRの中点まで（＝東側へ）シフトする
        END AS "MinX",
        "MinY",
        CASE -- 半分に分割する本来の位置はどちら側にあるか？
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX_0","MinY",("MaxX"+"MinX")/2,"MaxY")),1) >= "area_A"/2 -- 西側にある場合
                THEN ("MaxX"+"MinX")/2 -- 次のMBRの最大値（東端）を現在のMBRの中点まで（＝西側へ）シフトする
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX_0","MinY",("MaxX"+"MinX")/2,"MaxY")),1) <  "area_A"/2 -- 東側にある場合
                THEN "MaxX" -- 次のMBRの最大側（東端）は据え置き
        END AS "MaxX",
        "MaxY",
        "geom_0", -- ポリゴンA
        "area_A", -- ポリゴンAの面積
        ST_Area(ST_Intersection("geom_0",BuildMbr("MinX_0","MinY",("MaxX"+"MinX")/2,"MaxY")),1) AS "area_A_west", -- 西側で抽出したポリゴンAの部分の面積
        CASE -- 半分に分割する本来の位置はどちら側にあるか？
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX_0","MinY",("MaxX"+"MinX")/2,"MaxY")),1) > "area_A"/2 THEN 'west'
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX_0","MinY",("MaxX"+"MinX")/2,"MaxY")),1) < "area_A"/2 THEN 'east'
            WHEN ST_Area(ST_Intersection("geom_0",BuildMbr("MinX_0","MinY",("MaxX"+"MinX")/2,"MaxY")),1) = "area_A"/2 THEN 'half'
            ELSE 'unknown'
        END AS "west_or_east"
    FROM recursive_split
)
SELECT
    *,
    ABS(ST_Area(ST_Intersection("geom_0",BuildMbr("MinX_0","MinY",("MaxX"+"MinX")/2,"MaxY")),1) - "area_A"/2) AS "difference",
    MakeLine(
        MakePoint(("MaxX"+"MinX")/2,"MinY",4612),
        MakePoint(("MaxX"+"MinX")/2,"MaxY",4612)
    ) AS "geom_blade" -- 切断位置のラインを生成
FROM recursive_split
LIMIT 10
;

ずいぶん長ったらしいクエリになってしまいましたorz

WITH構文の中の recursive_split というサブクエリは

recursive_split AS (
    SELECT ほげほげ
    FROM recursive_split
)

という形で、自己参照になっていることがわかります。

このサブクエリの一回目の選択の部分は、ポリゴンAをMBRの西側半分で取り出した結果に応じて次の長方形の端点座標を取得しています。

• 本来の分割位置が東側だった場合は、長方形の西側端点（MinX）を東側半分の端点（(MinX+MaxX)/2）にシフトし、東側端点（MaxX）は据え置き
• 本来の分割位置が西側だった場合は、長方形の西側端点（MinX）は据え置き、東側端点（MaxX）を西側半分の端点（(MinX+MaxX)/2）にシフト

UNION ALL より後も、だいたいは一回目の選択と同じものですが、ポリゴンAの部分を抽出する際には、常に西側の端点をポリゴンAの西側端点にする必要があるため、これを MinX_0 としています。

最後のSELECT文では、ポリゴンAの面積の半分と、各回の分割結果との差分を取得しています。
また、その際の分割線も生成しています。（MakeLine()の部分）

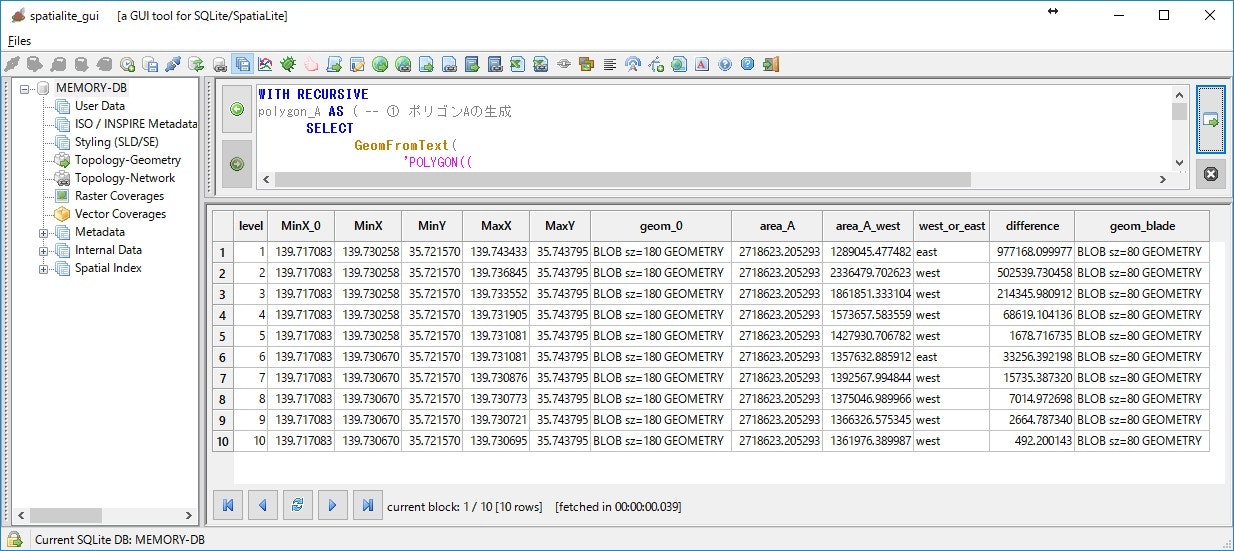
結果は以下のようになります。

分割が進むにつれて、本来の等分面積との差（difference）が小さくなっているのがわかります。
10回の再帰で差分は492m2になりました。ポリゴンAの面積は2.71km2なので、0.01％程度に相当します。

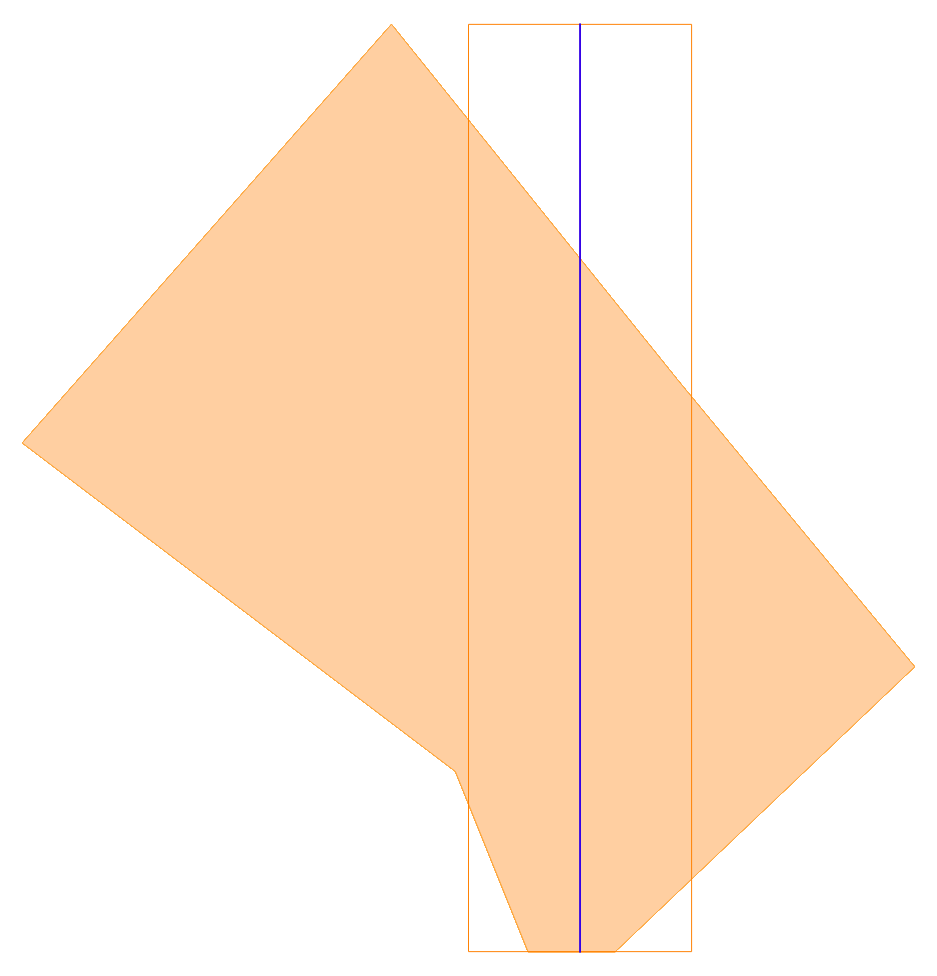
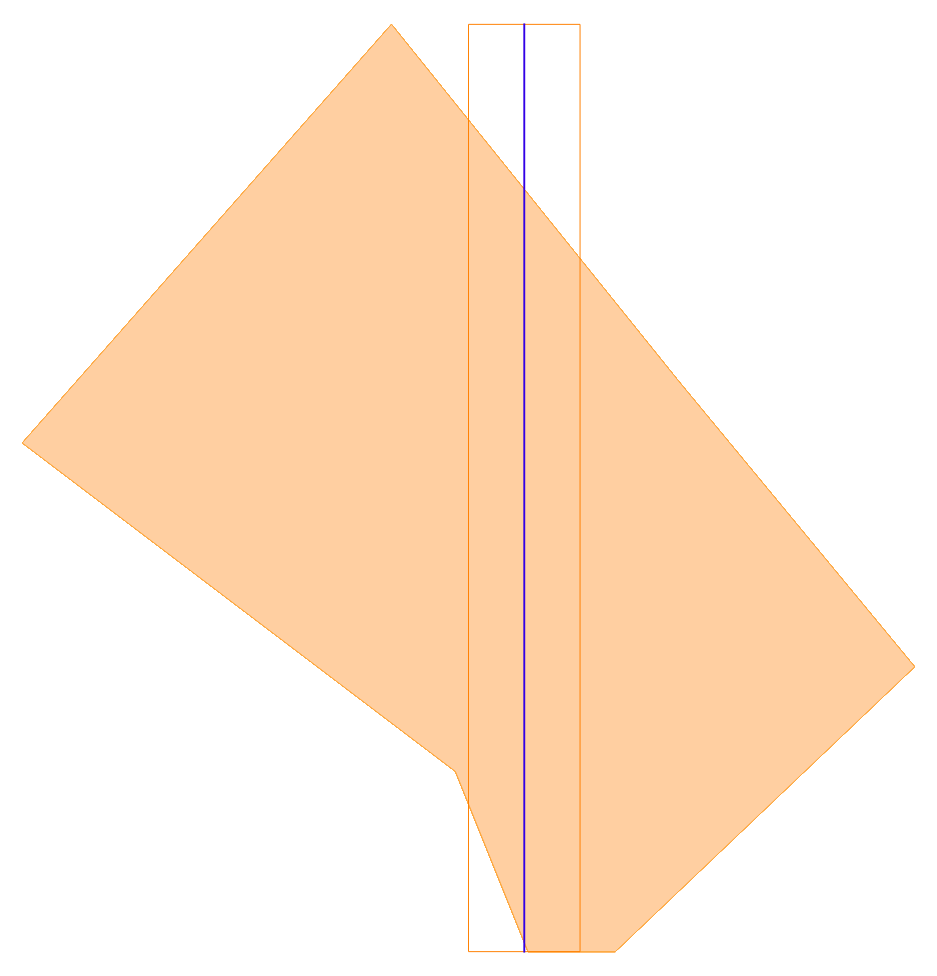
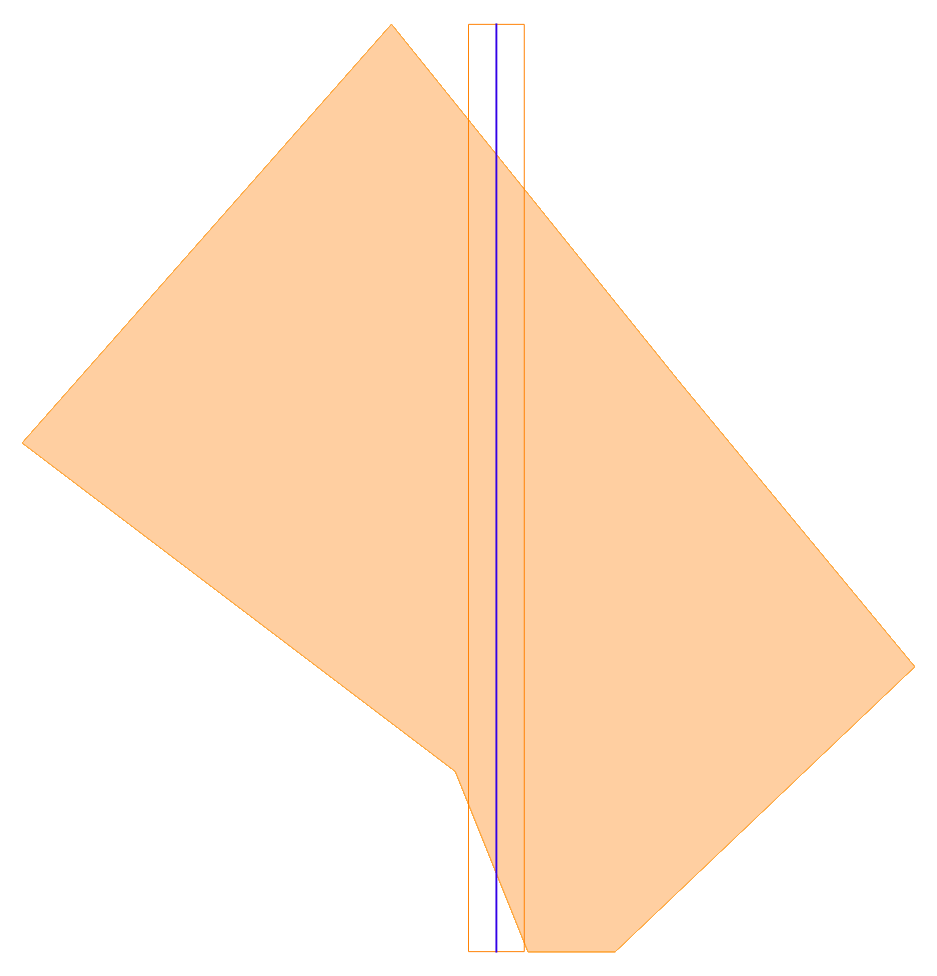
分割の様子を順番に図にしてみました。（オレンジの枠が現在の長方形、紫の線が分割線です。）

• 一回目
  

• 二回目
  

• 三回目
  

• 四回目
  

• 五回目
  

おしまい！
みなさま、良いお年をお迎えくださいませ！（早