内容
とある目的で、日付範囲から、日付範囲を除外したいことがありました。
例えば、
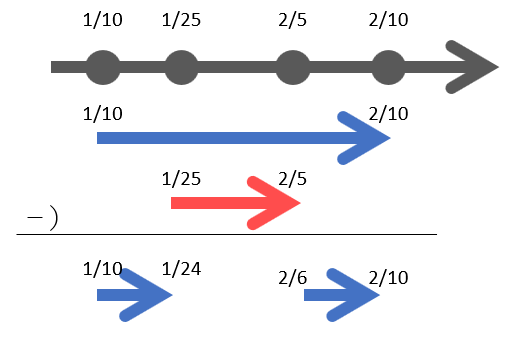
2023/1/10~2023/2/10 から
2023/1/25~2023/2/5 を除く
といった感じ。
期待する答えは、2023/1/10~2023/1/24と、2023/2/6~2023/2/10です。数直線を引くとわかりやすいです。
作ったもの
githubに置いておきました。
ちなみに、私は引き算が欲しかったので、足し算もあるな~と思いつつ、めんどくさいから作ってません。いつか作るかも。なのでこの記事では、差演算(と言っていいのかわからないけど)についてだけを書きます。
要件
まず入力として、①引かれる日付範囲と、②引く日付範囲があって、生きている①から、死んでしまう②範囲を除きます。なので上の数直線では、①は青(生きている)、②は赤(死ぬ)として、最終的に生きている範囲を求めます。赤の日は死ぬので、生きる日は赤の開始の前日、終了の翌日になります。
次に、①も②も、指定なしの要素ゼロでもよいし複数でもよい。つまり引数としては、開始と終了のペアを、配列で複数指定します。包含関係も制限なし。
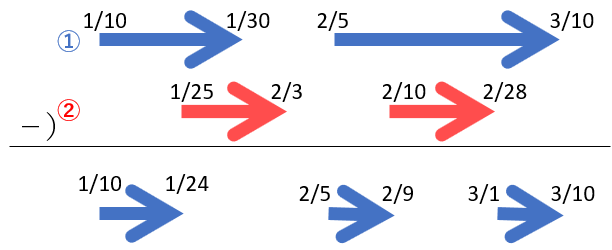
つまり、①としては1/10~1/30と2/5~2/28(複数)、②としては1/25~2/3と2/10~3/10(複数)とか、したいです。
考え方
概要
コンピューター的な考え方だと、ビット演算の差。「① NOT ( ① AND ② )」ですかね。今考えると、それを使うのがよかったかもしれません。。配列をずら~っと持つのもちょっとなーと思ってやめました。
人でやるとしたらどうかなーと思うと、①の要素を過去から見ていって、②の範囲になるまでが生きているとして、②にぶつかったらその前日まで、みたいな感じです。今回はそれで実装しました。かなり泥臭い。
以下では、泥臭い処理をどう整理したかを書いておきます。
パターン
①と②で、①<②、①=②、②<①の3パターンがあります。
①<②の場合(開始パターンA)は、①の開始日から生きる期間がありますが、①=②と②<①(開始パターンB)はありません。なのでここで2つに分岐。
開始パターンAの場合で、①の終了と②の開始の関係性が、①の終了<②の開始と①の終了=②の開始(終了パターンA)と、②の開始<①の終了(終了パターンB)があり、ここで2つに分岐。
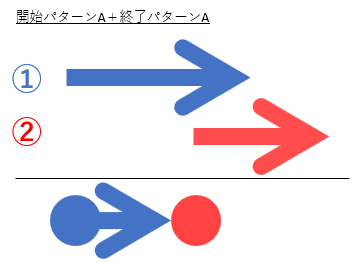
■開始パターンA+終了パターンAの場合
①の開始と、②由来の終了の期間が解です。
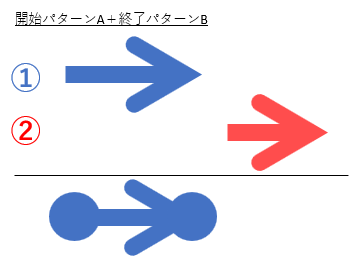
■開始パターンA+終了パターンBの場合
①の開始と、①の終了の期間が解です。
話を戻して、開始の関係性が②≦①(開始パターンB)の場合。この場合の終了パターンは、①の終了と②の終了を比較して分岐させました。
②の終了≦①の終了(終了パターンA)と、②の終了<①の終了(終了パターンB)。
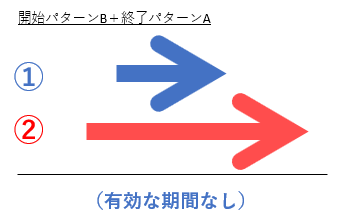
■開始パターンB+終了パターンAの場合
①が②に包含されているので、有効な期間はないです。
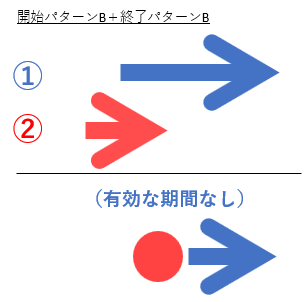
■開始パターンB+終了パターンBの場合
こちらも今すぐには有効な期間はないのですが、次の②に対して組み合わせのパターンを調べていきたいので、①の開始時期を②の終了の翌日に書き換えてしまいます。
まとめ
ざっくり書くとこんな感じでした。いやぁ・・・めんどくさい。けど、こういうのを地道に考える論理パズル的な要素って、SEには必要なことのように思います。イコールの場合はどっち?とか。
配列の操作(次の要素を取り出すタイミングとか)もなかなか難しいです。
なのでこの問題は、SEの新人研修とかでやらせたら面白いんじゃないかと思いました。今の子はググってこのページ見つけ出してしまうのかも。自分で生み出す訓練をしたいのに、やっかいな時代になりましたw