二項検定をする
A 君と B 君がポケモンで対決をしました。 20 回ほど遊んだ結果として A 君が 17 回勝利し、 B 君が 3 回勝利をしました。
感覚的に A 君のほうが明らかにポケモントレーナーとして強そうですが、果たして統計学的にも同じことが言えるでしょうか。今回は統計解析用の言語である R を利用してこれを仮説検定します。
統計解析用言語 R
R は自由なソフトウェアで、無料で使える統計解析用言語です。統計の分野では有償のソフトウェアも MATLAB など有名なものがたくさんありますが、いずれもなかなかに高価です。
その点 R は無料で使えますのでなかなか予算の確保できない貧乏な研究者にもやさしいですし、それでいて柔軟で強力な機能を備えていますから、この言語を習得して損することは無いと言っても差し支えないほどです。
さて一連の記事では Python を主に使ってきましたが、純粋に統計解析という観点で Python と R を比較すると、可視化や数値解析の手軽さや豊富さという点で R に軍配が上がるのではないかと筆者は感じています。
今まで Python を使ってきた理由としては、それがグルー言語として万能であること、他の処理と連携する際に統一された言語で全体を記述できることといった点が挙げられます。
したがいまして、純粋に数値解析やその可視化をする必要に迫られるといった場面では R を使うと良いかと思います。
帰無仮説と対立仮説の設定
さてまずは仮説の設定です。仮説については以前に説明した通りですね。この例の場合ではこうなります。
| 仮説 | 説明 |
|---|---|
| 帰無仮説 | A 君と B 君の実力は等しい |
| 対立仮説 | A 君は B 君より強い |
対立仮説では実力が等しくない、ではなく片側検定にあたる A 君が強いかどうかという設定をします。
検定する統計量は A 君の勝利数とします。この場合、 A 君の手持ちのポケモンが何かといったことや、不正が無いかどうかといったことは考慮しません。統計量の実現値は勝利数である 17 です。
検定統計量の分布を求める
R の dbinom 関数は n 回の試行中 x 回成功するかを求めることができます。式は dbinom( 成功数, 試行数, 成功確率 ) となります。この場合成功確率は勝つか負けるかしかありませんので 0.5 です。いわゆる二項検定となります。
dbinom (17, 20, 0.5)
# => [1] 0.001087189
もし両者の実力が等しいとすると 17 勝 3 敗となる確率はわずか 0.1% です。この時点で結果が明らかなような気もしなくも無いですがもう少し統計学的観点から調べてみましょう。
前述の dbinom 関数には数値ベクトルを含めることができます。
wins <- 0:20
dbinom(wins, 20, 0.5)
# =>
# [1] 9.536743e-07 1.907349e-05 1.811981e-04 1.087189e-03 4.620552e-03
# [6] 1.478577e-02 3.696442e-02 7.392883e-02 1.201344e-01 1.601791e-01
# [11] 1.761971e-01 1.601791e-01 1.201344e-01 7.392883e-02 3.696442e-02
# [16] 1.478577e-02 4.620552e-03 1.087189e-03 1.811981e-04 1.907349e-05
# [21] 9.536743e-07
帰無分布が表示されました。ベクトルは 0 から開始されているので 18 版目の数値 1.087 を見ます。 plot は R のプロッティング関数です。次のように使います。
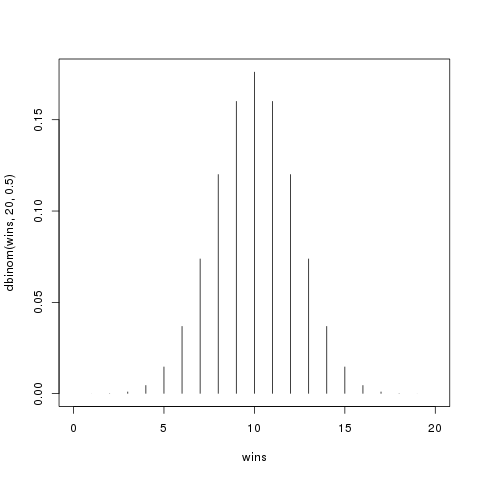
plot(wins,dbinom(wins, 20, 0.5), type="h")
png("image.png", width = 480, height = 480, pointsize = 12, bg = "white", res = NA)
この図があらわしているのは A 君と B 君の実力が五分である (= 帰無仮説) ときの 0 勝から 20 勝までのそれぞれの確率です。
pbinom 関数は勝利数が x 以下である確率 (= 下側確率) を求めます。片側検定なので下側確率を求めるわけですね。
round(pbinom(wins, 20, 0.5),4)
# =>
# [1] 0.0000 0.0000 0.0002 0.0013 0.0059 0.0207 0.0577 0.1316 0.2517 0.4119
# [11] 0.5881 0.7483 0.8684 0.9423 0.9793 0.9941 0.9987 0.9998 1.0000 1.0000
# [21] 1.0000
つまり 13 勝以下となる確率が 94.23% 、 14 勝以下となる確率が 97.93% です。 P 値は 16 勝以下となる確率を求める (17 ではない) ので、次のようになります。
pbinom(16,20,0.5)
# => [1] 0.9987116
これを 1 から引いて求まる P 値 0.001288 は有意水準 0.05 より小さいので帰無仮説が棄却され A 君がおそらく強いであろうと統計学的観点から言えることになります。
参考
Rによるやさしい統計学
http://www.amazon.co.jp/dp/4274067106