7/30~8/4にかけてカナダのバンクーバーで自然言語処理の国際学会である「ACL2017」が開催されました。
その中で要約の文脈でキーフレーズ抽出のアルゴリズム「PositionRank」が発表されていたので、実装してarXivの論文からキーフレーズ抽出を行ってみました。
元の論文とGithubのリポジトリは以下になります。
PositionRank: An Unsupervised Approach to Keyphrase Extraction from Scholarly Documents
ymym3412/position-rank
PositionRankとは
PositionRankは学術論文のタイトル(Title)と概要(Abstract)からキーフレーズを抽出するアルゴリズムです。
アルゴリズムはシンプルなので、学術論文以外にも適用が可能です。
また論文では英語の論文を対象にしていますが、Tokenizerを変えれば英語以外の言語でも適用可能です。
PositionRankのアルゴリズム
隣接行列の計算
PositionRankはPageRankなどと同じグラフベースのアルゴリズムです。
PageRankではグラフのノードはWebページでしたが、PositionRankでは文章中の単語となっています。
ノード$v_i$とノード$v_j$を結ぶエッジの重みは文章中で単語$v_i$と単語$v_j$が共起(単語$v_i$の文脈窓幅内に単語$v_j$がある)回数です。
これより単語をノードとしエッジの重みが共起回数である隣接行列Mを得ます。
そしてノードから出ているエッジの重みを別のノードへの遷移確率として解釈するために正規化を行った隣接行列$\tilde{M}$
を計算します。正規化の計算は以下のように行われます。$|V|$は対象文章中の単語の種類の数です。
\tilde{m_{ij}} = \left\{
\begin{array}{ll}
m_{ij} / \sum_{j=1}^{|V|}m_{ij} & (\sum_{j=1}^{|V|}m_{ij} \neq 0) \\
0 & (otherwise)
\end{array}
\right.
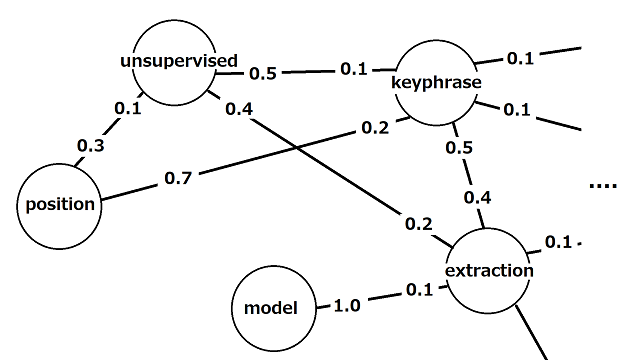
正規化された隣接行列 $\tilde{M}$ が表すグラフは以下のようなイメージです。
PositionRankを保持するベクトルと解釈
次にPositionRankのスコアを保持するベクトル$S \in \mathbb{R}^{|V|}$を用意します。
このベクトル$S$の初期値はすべて$\frac{1}{|V|}$とします。後述しますが一連の計算を終えたベクトル$S$の$i$番目の成分が単語$v_i$のPositionRankスコアです。
PageRankではスコアを保持するベクトル$S$と正規化された隣接行列$\tilde{M}$を使ってt+1ステップにおけるPageRankのスコアを以下のように計算していました。
S(t+1) = \tilde{M} \cdot S(t)
PositionRankのスコアもPageRankと同じようにステップtにおけるベクトル$S(t)$に隣接行列$\tilde{M}$を使って再帰的に計算をすることで求めることができます。
このベクトル$S(t+1)$の$i$番目の成分は、例えばグラフ上をエッジの重みに従って確率的に移動していくことを考えた際に、時刻$t+1$でノード$v_i$にいる確率を表しています。つまりグラフを確率的に移動しながら最終的に行く着く確率が高いノードはスコアが高いということです。
上記の計算を繰り返し行っていくことで、ベクトル$S$は特定の値(主固有ベクトル:principal eigenvector)に収束することが知られています。
PositionRankの解釈も同様でグラフを確率的に移動し最終的に行き着く確率が高いノードがPositionRankのスコアの高いノード(=単語)ということになります。
Damping factor
グラフベースのスコアリングアルゴリズムではグラフを移動しながらスコアが高いノードに収束していくわけですが、グラフの中にぐるぐる回り続けて出られなくなってしまうような巡回構造があると、正しくグラフの中を移動することができません。そこでその巡回構造を抜け出すために「テレポート」するような処理を加えます。
S(t+1) = \alpha \cdot \tilde{M} \cdot S(t) + (1 - \alpha) \cdot \tilde{p}
$\tilde{p} \in \mathbb{R}^{|V|}$はどのノードにテレポートするかの確率を保持するベクトルです。$\alpha$はdamping factorといい、隣接行列に沿った移動の確率とテレポートの確率の割合を制御するパラメータです。
PositionRankの計算
先ほどテレポートの確率を保持するベクトル$\tilde{p}$がありましたが、このベクトルに各単語の出現位置に応じたバイアスを載せていきます。
まずベクトル$\tilde{p}$の計算に必要な各単語$v_i$に関するスコアを計算していきます。このスコアは文章の先頭から数えた単語の出現位置の逆数の和として計算されます。例えば単語$v_i$が2番目、5番目、10番目に出現したとしたら、$v_i$のスコア$p_i$は次のように計算します。
p_i = \frac{1}{2} + \frac{1}{5} + \frac{1}{10} = \frac{4}{5} = 0.8
このようにして計算した各単語のスコアを元に、最終的な$\tilde{p}$を次のように計算します。
\tilde{p} = \Biggl[ \frac{p_1}{\sum_{i=1}^{|V|}p_i}, \frac{p_2}{\sum_{i=1}^{|V|}p_i}, ..., \frac{p_{|V|}}{\sum_{i=1}^{|V|}p_i} \Biggr]
このバイアスを加えたベクトル$\tilde{p}$は「タイトルやアブストラクトの序盤に出現する単語は重要な単語であるだろう」という発想を組み込んでいると言えます。単語の出現位置に応じたバイアスを乗せるというのがこのPositionRankのキーポイントです。
このベクトル$\tilde{p}$を使ってある時刻における単語$v_i$のPositionRank:$S(v_i)$(=ベクトル$S$の第$i$成分)を以下のように定義します。
S(v_i) = (1 - \alpha) \cdot \tilde{p_i} + \alpha \cdot \sum_{v_j \in Adj(v_i)} \frac{w_{ji}}{O(v_j)}S(v_j) \\
※ただしO(v_j) = \sum_{v_k \in Adj(v_j)}w_{jk} \\
※Adj(v_i)はv_iの隣接点の集合
この計算を100ステップ、あるいは1ステップ前とのベクトル$S$との差が0.001より小さくなるまで計算を行えばベクトル$S$がPositionRankのスコアとなります。
なおキーフレーズの品詞は「形容詞」と「名詞」に限定しています。
また単語単位ではなく「Markov chain Monte Carlo methods」のように長いフレーズも抽出できるように、連続する単語のPOSが(adjective)*(noun)+のパターンとなっているものをフレーズとし、フレーズのPositionRankスコアをフレーズ内の単語のPositionRankのスコアの和としています。
PositionRankの実装
実装はGithubで公開しています。ここではPositionRankを計算するコードにインラインでコメントをつけて簡単な解説だけ行います。
import math
import stemming.porter2 as porter
import numpy as np
import copy
from collections import Counter
def position_rank(sentence, tokenizer, alpha=0.85, window_size=6, num_keyphrase=10, lang="en"):
"""
Args:
sentence: TitleとAbstract
tokenizer: 文章を単語区切りにするtokenizer。
リポジトリには英語向けのtokenizerとMecabを使った日本語向けtokenizerがある。
alpha: Damping factor
window_size: 文脈窓幅
num_keyphrase:抽出したいキーフレーズの数
Returns:
キーフレーズのリスト
"""
if lang == "en":
# 英語の場合ステミングを行う。
stem = porter.stem
else:
stem = lambda word: word
# 単語のリストとフレーズにリスト
original_words, phrases = tokenizer.tokenize(sentence)
stemmed_word = [stem(word) for word in original_words]
unique_word_list = set([word for word in stemmed_word])
n = len(unique_word_list)
adjancency_matrix = np.zeros((n, n))
word2idx = {w: i for i, w in enumerate(unique_word_list)}
p_vec = np.zeros(n)
# 単語wの共起単語を保持する辞書
co_occ_dict = {w: [] for w in unique_word_list}
# ベクトルpの計算と共起単語の収集
for i, w in enumerate(stemmed_word)
# 出現位置の逆数を加算
p_vec[word2idx[w]] += float(1 / (i+1))
# 窓は前後
for window_idx in range(1, math.ceil(window_size / 2)+1):
if i - window_idx >= 0:
co_list = co_occ_dict[w]
co_list.append(stemmed_word[i - window_idx])
co_occ_dict[w] = co_list
if i + window_idx < len(stemmed_word):
co_list = co_occ_dict[w]
co_list.append(stemmed_word[i + window_idx])
co_occ_dict[w] = co_list
# 単語vi(w)とvj(co_word)の共起回数を数えて隣接行列Mを生成
for w, co_list in co_occ_dict.items():
cnt = Counter(co_list)
for co_word, freq in cnt.most_common():
adjancency_matrix[word2idx[w]][word2idx[co_word]] = freq
# 正規化した隣接行列M~を生成
adjancency_matrix = adjancency_matrix / adjancency_matrix.sum(axis=0)
# p_iのスコアの和で除算してP~ベクトルを得る
p_vec = p_vec / p_vec.sum()
# ベクトルSを1/|V|で初期化
s_vec = np.ones(n) / n
# threshold
lambda_val = 1.0
loop = 0
# 100ループ終えるか1時刻前のベクトルSとの差が0.001を下回るまで計算する
while lambda_val > 0.001:
next_s_vec = copy.deepcopy(s_vec)
for i, (p, s) in enumerate(zip(p_vec, s_vec)):
next_s = (1 - alpha) * p + alpha * (weight_total(adjancency_matrix, i, s_vec))
next_s_vec[i] = next_s
lambda_val = np.linalg.norm(next_s_vec - s_vec)
s_vec = next_s_vec
loop += 1
if loop > 100:
break
word_with_score_list = [(word, s_vec[word2idx[stem(word)]]) for word in original_words]
# フレーズに対するスコアを計算
for phrase in phrases:
total_score = sum([s_vec[word2idx[stem(word)]] for word in phrase.split("_")])
word_with_score_list.append((phrase, total_score))
# スコア順にソートされたインデックスのリスト
sort_list = np.argsort([t[1] for t in word_with_score_list])
keyphrase_list = []
# ステミングした結果が同じ単語の排除
stemmed_keyphrase_list = []
for idx in reversed(sort_list):
keyphrase = word_with_score_list[idx][0]
stemmed_keyphrase = " ".join([stem(word) for word in keyphrase.split("_")])
if not stemmed_keyphrase in stemmed_keyphrase_list:
keyphrase_list.append(keyphrase)
stemmed_keyphrase_list.append(stemmed_keyphrase)
if len(keyphrase_list) >= num_keyphrase:
break
return keyphrase_list
def weight_total(matrix, idx, s_vec):
"""
\sum_{v_j <- Adj(v_i)} \w_{ji}/O(v_j) * S(v_j)の計算を行う
"""
return sum([(wij / matrix.sum(axis=0)[j]) * s_vec[j] for j, wij in enumerate(matrix[idx]) if not wij == 0])
arXiv論文からキーフレーズ抽出
では最後にPositionRankを使っていくつかのarXivの論文からキーフレーズを抽出してみようと思います。論文の選択は独断に基づいており特に他意はありません。
PositionRank: An Unsupervised Approach to Keyphrase Extraction from Scholarly Documents
まずはPositionRankの論文自身からキーフレーズ抽出を行ってみようと思います。
Title: PositionRank: An Unsupervised Approach to Keyphrase Extraction from Scholarly Documents
Keyphrase is ...
PositionRank, online_scholarly_data, fast_information_processing, account_word_positions, Keyphrase, Extraction, Approach, Unsupervised, document, Scholarly
学術論文に対して行うこと、キーフレーズの抽出、教師なしの手法であることなどがうまく抽出できているのではないでしょうか。
Attention Is All You Need
NLP界隈でちょっと話題になった論文です。名前がかっこいいですね。
Title: Attention Is All You Need
Keyphrase is ...
best_models, model, machine_translation_tasks, convolutional_neural_networks, Englishto-German_translation_task, English-to-French_translation_task, attention_mechanism, dominant, other_tasks, sequence
CNNを使った機械翻訳であること、attentionを使ったモデルであることが分かると思います。
Diversity driven Attention Model for Query-based Abstractive Summarization
私が好きな文書要約領域の論文です。
Title: Diversity driven Attention Model for Query-based Abstractive Summarization
Keyphrase is ...
Query-based_Abstractive_Summarization, Abstractive_summarization, Attention_Model, query-based_summarization_task, query-based_summarization, Abstractive, query_attention_model, extractive_summarization, Query-based, summarization
クエリベースの生成型要約手法であることがよく抽出できていると思います。ただ「query」のスコアが高いのか何度も出現してしまっているため、他に有用な情報を落としてしまっている可能性もあると思います。
おまけ: 日本語論文からキーフレーズ抽出
Githubのposition_rank()メソッドは渡すtokenizerを言語に合わせて変更すれば日本語に論文に対しても実行できます。日本語へはMecabを利用したMecabTokenizerというクラスを用意しています。
ここでは5月に開催された人工知能学会の論文から1つピックアップしてPositionRankでキーフレーズ抽出をしてみようと思います。
Title: 文書分類とのマルチタスク学習による重要文抽出
Keyphrase is ...
重要文抽出実験, 重要文抽出, 重要文手法, マルチタスク学習モデル, 商品レビュー文, 文, 自動文書要約, 抽出, 文書分類, 学習, 重要, 要約, 推定タスク間, マルチタスク, 汎化性能
おわりに
今回はACL2017で発表されたキーフレーズ抽出手法「PositionRank」についてアルゴリズムと実装の解説を行いました。
ACLには会社の後輩が参加しており、参加報告レポートを後日公開予定ですのでそちらも見て頂ければと思います。
面白いなと感じて頂けたら、GithubでStarなどして頂けると嬉しいです!
参考文献
PositionRank: An Unsupervised Approach to Keyphrase Extraction from Scholarly Documents
Attention Is All You Need
Diversity driven Attention Model for Query-based Abstractive Summarization
文書分類とのマルチタスク学習による重要文抽出
自動要約アルゴリズムLexRankでドナルド・トランプ氏の演説を3行に要約してみる