テキスト要約モデルの評価では、ROUGEと呼ばれる評価指標を用いるのが一般的です。
論文ではROUGEを使用してモデル評価を行うことがほとんどですが、ROUGEでは測れないようなモデルの側面を捉えるためには異なる評価指標も必要となってきます。
この記事では要約モデルを評価するROUGEとは異なる手法について解説していきます。
紹介する論文はこちらなのですが、論文中に手法の名前は特に言及されていないようなので、ここでは著者がGithubにコードを上げているリポジトリの名前から取って「theta evaluation」と呼んでいきます。
あれどっかで似たような記事を読んだような?という方、鋭いです。
実は自然言語処理 Advent Calendar 2017 1日目の記事も要約モデルの評価指標に関する記事です。
1日目の記事とはまた違った手法を解説しているので良かったら読んでください。
1日目の記事はこちらです。ROUGEについて知りたい方はこちらをご参照ください。
ROUGEを訪ねて三千里:より良い要約の評価を求めて
theta evaluationってどんな手法?
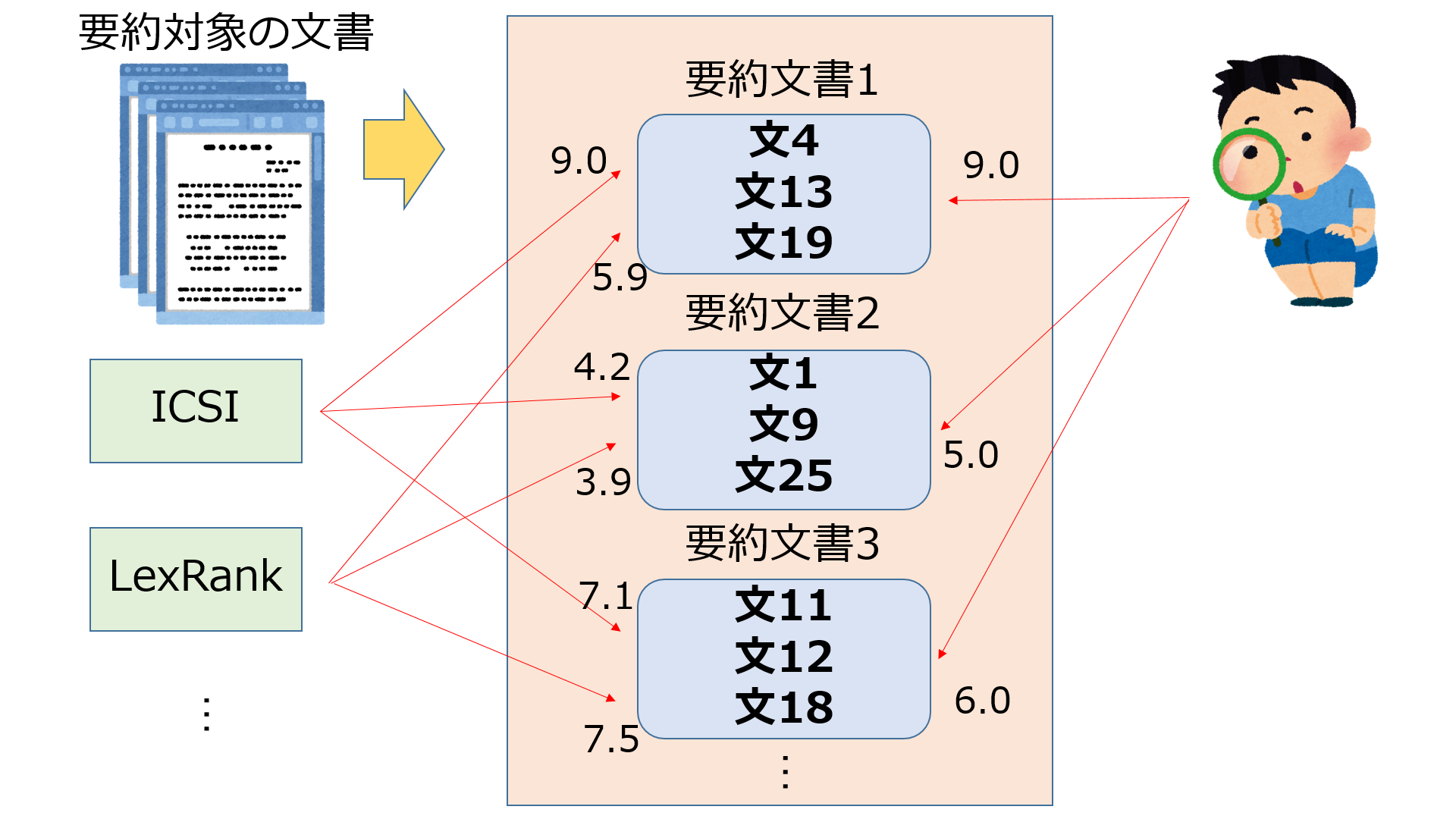
theta evaluationは抽出型要約手法を人手でのスコアリングとの相関を使って評価する手法です。
theta evaluationでは、抽出型要約手法を$\theta$関数及び最適化手法$O$の2つに分解し、この$\theta$関数と人間の評価の相関を計測することでモデルの評価としていきます。
ではこの分解と相関による計測について、順番に解説していこうと思います。
(θ, O)分解
theta evaluationは抽出型要約の手法を「要約文をスコアリングする関数: $\theta$」と「$\theta$でスコアリングされた要約文の集合から最もスコアが高い要約を見つける最適化手法: $O$」の2つに分解していきます。
要約対象の文書$D$を$D = \{ {s_1, s_2, ..., s_D} \}$のように文の集合とします。このとき要約文書$S$はドキュメントに含まれる文をいくつか抽出したものになるので、$S$は$D$の部分集合になります。
$\theta$関数は要約文書を受け取り実数値を返すような関数です。
つまり、要約文書は元の文書からいろんな文を抜き出して作成されますが、$\theta$関数はそれぞれの要約文書にスコアリングを行うということです。
\begin{array}{r@{\;}ll}\\
\theta : &S &\mapsto \theta_D(S) &( ただし\theta_D(S) \in \mathbb{R}) \\
\end{array}
最適化手法$O$は、何らかの制約下のもとで$\theta$関数を使ってスコアリングされた要約文書の中からスコアが最大の要約文書を探す役割を持っています。要約生成では、生成する要約に長さの制限を持たせることが一般的なので、$O$は与えられた長さ$c$に対してこの長さを超えない要約文書の中からスコアが最大の要約文書を探し出します。
$O$は$\theta$関数と文書を受け取り、最適な要約文書$S^*$を見つける関数として表現できます。
\begin{array}{r@{\;}ll}\\
O : (\theta, D) \mapsto S^*
\end{array}
抽出型要約の手法は、この$\theta$関数と最適化手法$O$の2つに分解することができます。
θ関数の例
既存の手法がどのように分解できるのかちょっと見てみます。
ICSI
ICSIは文に含まれるn-gramに重み付けをし、要約文書に含まれるn-gramと重みによるスコアの和が最大となるような要約文書を最大被覆問題として求める手法です。ICSIはROUGEベースの評価では最も良いスコアを残しているモデルです。ICSIにおける$\theta$関数はn-gramと重みを使って次のように表現できます。
\theta_{ICSI}(S) = \sum_{c_i \in S} c_i * w_i
LexRank
LexRankはPageRankに似たグラフベースの抽出型要約の手法です。グラフのノードが文となっており、PageRankを求める方法で文のスコアリングを行います。つまりLexRankにおける$\theta$関数は要約文書に含まれる文のPageRankの和を求める関数として表現できます。
\theta_{LexRank}(S) = \sum_{s \in S} PageRank(s)
人間の評価との相関
($\theta$, $O$)分解より、抽出型要約手法は文書をスコアリングする$\theta$関数を持つことが分かりました。
そこで要約文書に対して、人間がつけるスコアリングと各手法がつけるスコアリングの相関を分析するのがtheta evaluationのキモになります。
各手法のスコアと人間のスコアに対して、「ピアソン積率相関」「スピアマン順位相関」「Ndcg」の3つの尺度を使って評価します。
Ndcgはランキングを行うアルゴリズムの評価に使われる指標で、ランキング上位の要素を正解した際の得点が下位と比べて強調されるような尺度です。
評価結果
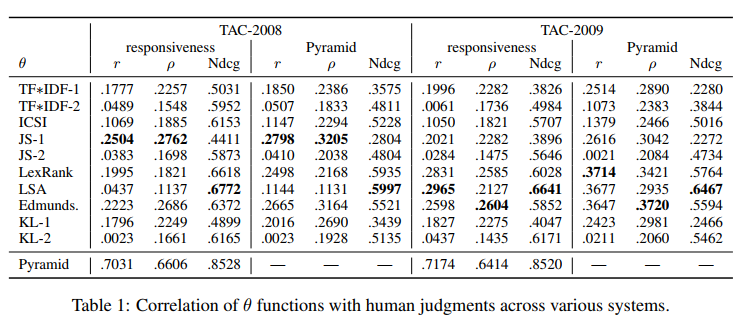
実際にTACという要約タスク用のデータセットを使って各手法と人間のスコアリングの相関を計測した結果を見ていきましょう。
「responsiveness」及び「Pyramid」は各要約に付与されている人手のスコアです。
この結果を見るといくつか興味深い点が見えてきます。
1つはピアソン積率相関係数やスピアマン順位相関係数が全体的に低い一方で、Ndcgの数値は比較的高いということです。
この結果は以下のように解釈することができます。
ROUGEスコアでモデルを評価する場合、使用されるのはモデルが最もスコアが高いと判断したベストな要約のみです。つまりROUGEで高い数値を記録するモデルは人手で最も高いスコアを記録する要約を抽出してくることは得意です。
しかし既存の手法では、あらゆる要約文書候補をスコアリングした際にベストな要約文書はうまくスコア付けできるがそれ以外の要約文書はうまくスコアリングできていないために、このような相関係数の差が生まれてしまっています。
おわりに
この記事では抽出型要約手法の新しい評価方法としてtheta evaluationを紹介しました。
ここからはtheta evaluationとROUGEについて少し私見を書いていこうと思います。
まずtheta evaluationとROUGEの関係についてですが、theta evaluationはROUGEの代替を目指した指標ではないと思っています。
ROUGEはそのモデルが参照要約をどれだけ再現できるかを評価しています。
参照要約は作成者にとって最もスコアが高い要約なので、ROUGEはその最もスコアが高い要約1つを抽出出来るかを見ていると言えます。
実務で要約システムを使う上ではユーザーに提供する要約は(おそらく)1つのみですし、その1つの要約を評価できているという点ではROUGEで要約モデルを評価することには妥当だと思います。
対してtheta evaluationは各手法の$\theta$関数を通して、人間の評価との相関を評価しています。
これは$\theta$関数が人間の評価をうまくモデリングできているかを測っていると考えることができます。
つまりtheta evaluationが高いモデルというのは、あらゆる要約文書に対して人間がどう判断を下すかをうまくモデリング出来ているということです。
theta evaluationが高いモデルを深く分析することで、人間がどういった要約を良いと判断するかを調べることができると思います。
なのでROUGEとtheta evaluation、この2つの評価指標でモデルを評価し分析していくことで抽出型要約技術の研究がより先に加速していくのではないかと考えています。
最後に、この記事が自然言語処理に興味のある方々のお役に立てば幸いです。
参考資料
A Principled Framework for Evaluating Summarizers: Comparing Models of Summary Quality against Human Judgments
UKPLab/acl2017-theta_evaluation_summarization / Github
A Scalable Global Model for Summarization
The ICSI Summarization System at TAC 2008
Introduction to Automatic Summarization / SlideShare
Automatic summarization / SlideShare
ROUGEを訪ねて三千里:より良い要約の評価を求めて