Cirq で Superdense coding を実装
Quantum Computing and Quantum Information(QCQI) を読んでいて面白いアルゴリズムを見つけたので Cirq で実装してみました。
Superdense coding とは
概略
二者間の通信において、 1 量子ビットを送信するだけで、古典 2 ビットの情報を送信できるプロトコルになります。
※ IBM の研究者が論文で発表しています。
Alice と Bob
Supserdense coding では以下のステップで Alice から Bob に 1 量子ビットを送信することで、古典 2 ビットの情報を Alice から Bob へ伝達します。
※ 暗号や通信の話になると、だいたい Alice と Bob がでてきますね。ちなみに wikipedia に出てくるキャラクター一覧が乗っています。Alice はたいてい Bob にメッセージを送り、Eve がそれを盗聴するのが主な役割でみたいです。。。
- $ \left| 0 \right> $ の状態の量子ビットを2つ用意する。
- 上記の量子ビットを Bell 状態にする。
- Bell 状態になっている量子ビットを Alice と Bob に1つずつ渡す。
- Alice は**送信したいメッセージ(00, 01, 10, 11)**に応じて、上記で渡された量子ビットを操作する。
- 操作した量子ビットを Alice から Bob に送信する。
- Bob が Alice から受信した量子ビットと 3. で渡された量子ビットを測定して、Alice のメッセージを受け取る。
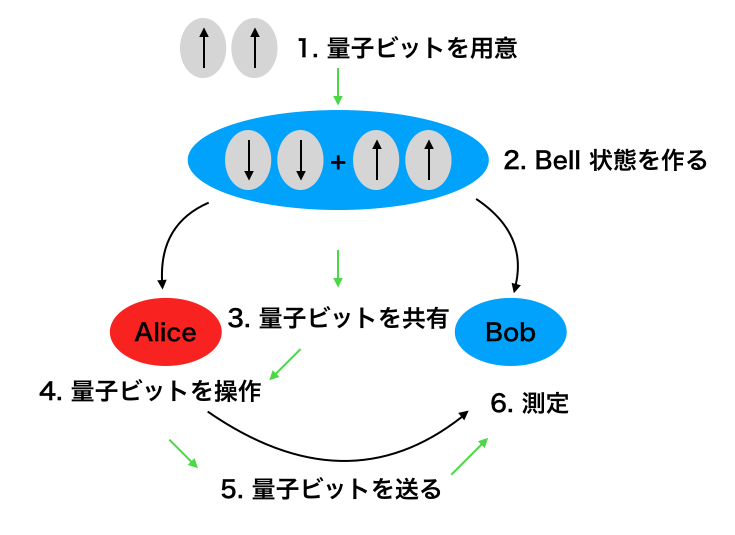
黒の矢印が量子ビットの動きで緑の矢印が操作の流れになります。
4.で行う Alice が行う操作は以下の表でまとめられます。
※ 例えば、01 を送信したい場合は、4.のステップで Alice の持っている量子ビットに $ X $ を作用させることになります。
| Alice が送信したい情報 | 量子ビットへの操作 |
|---|---|
| 00 | $ 1 $ |
| 01 | $ X $ |
| 10 | $ Z $ |
| 11 | $ iY = XZ $ |
量子計算
サーキット
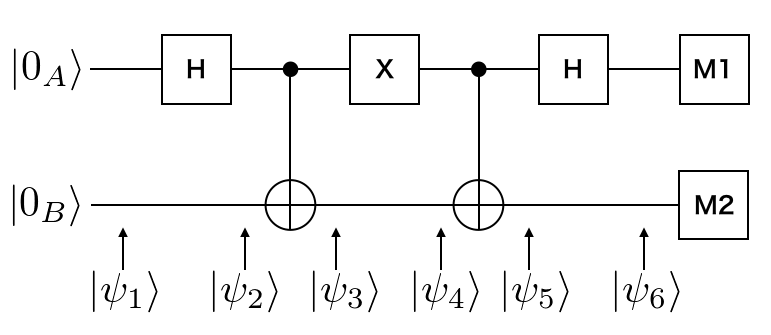
サーキット図は以下になります。
※ Alice が Bob に 01 を送る場合で、各モーメントでの量子ビットの状態を $ \left| \psi_{n} \right> \left( n = 1,2,3,4,5,6 \right)$ で記載しました。
$ \left| \psi_{3} \right> $ と $ \left| \psi_{4} \right> $ の間で Alice の持っている量子ビットに操作させている $ X $ を変えることによって Bob に送るメッセージを変えることができます。
※ 送信したい情報と量子ビットへの操作の対応は先程記載した表になります。
Alice が Bob に 01 を送る場合の各モーメントの状態
各モーメントで量子ビットへの操作を計算すると量子ビットの状態は以下のようになります。
\begin{align}
\left| \psi_{1} \right> &= \left| 0_{A} \right> \left| 0_{B} \right> \\
\left| \psi_{2} \right> &= H \otimes 1 \left| \psi_{1} \right> = \frac{1}{\sqrt{2}} \bigl( \left| 0_{A} \right> + \left| 1_{A} \right> \bigr) \left| 0_{B} \right> \\
\left| \psi_{3} \right> &= CNOT \left| \psi_{2} \right> = \frac{1}{\sqrt{2}} \bigl( \left| 0_{A} \right> \left| 0_{B} \right> + \left| 1_{A} \right> \left| 1_{B} \right> \bigr) \\
\left| \psi_{4} \right> &= X \otimes 1 \left| \psi_{3} \right> = \frac{1}{\sqrt{2}} \bigl( \left| 1_{A} \right> \left| 0_{B} \right> + \left| 0_{A} \right> \left| 1_{B} \right> \bigr) \\
\left| \psi_{5} \right> &= CNOT \left| \psi_{4} \right> = \frac{1}{\sqrt{2}} \bigl( \left| 1_{A} \right> \left| 1_{B} \right> + \left| 0_{A} \right> \left| 1_{B} \right> \bigr) \\
\left| \psi_{6} \right> &= H \otimes 1 \left| \psi_{5} \right> = \left| 0_{A} \right> \left| 1_{B} \right> \\
\end{align}
Cirq での実装
Cirq で上記の量子サーキットを実装すると以下になります。
from cirq import GridQubit, Circuit, Simulator, measure
from cirq.ops import X, Z, H, CNOT
q0, q1 = [GridQubit(0, x) for x in range(2)]
def create_circuit_of_superdense_coding(sending_bit, meas=True):
if sending_bit not in ['00', '10', '01', '11']:
raise Exception('sending_bit (%s) is invalid value' % sending_bit)
yield H(q0)
yield CNOT(q0, q1)
if sending_bit == '00':
# when Alise send 00 to Bob, then operate unit matrix
pass
elif sending_bit == '01':
yield X(q0)
elif sending_bit == '10':
yield Z(q0)
elif sending_bit == '11':
# operate iY = XZ
yield Z(q0), X(q0)
yield CNOT(q0, q1)
yield H(q0)
if meas:
yield measure(q0, key='q0'), measure(q1, key='q1')
SENDING_BIT = '01'
try:
circuit = Circuit()
circuit.append(create_circuit_of_superdense_coding(SENDING_BIT))
print('circuit:\n%s\n' % circuit)
simulator = Simulator()
print('measure:\n%s' % simulator.run(circuit))
except Exception as e:
print(e)
実行すると以下の結果になり、Alice から Bob に古典 2 ビットの情報が送信されたことになります。
circuit:
(0, 0): ───H───@───X───@───H───M('q0')───
│ │
(0, 1): ───────X───────X───────M('q1')───
measure:
q0=0
q1=1
※ 上記の実装は github にあげています。
まとめ
cirq を使って Superdense coding を実装し、 1 量子ビットを送信するだけで、古典 2 ビットをメッセージとして乗せられることを確認しました。
実際にプロトコルとして実装するには、 通信を行うたびに Alice と Bob に量子ビットを共有する方法等、いろいろと考えないといけないことが多いと思いますが、量子エンタングルメントを利用していて、物理的にも面白いアルゴリズムだと思いました。