問題設定
実正方行列 $A \in M(d, \mathbb{R}) \cong \mathbb{R}^{d \times d}$ が固有値 $\lambda \in \mathbb{C}$ を持ち, $v \in \mathbb{C}^d$ が対応する固有ベクトルとなるとする.
この時 $Av = \lambda v$ であり, $\lambda, v$ が実ならば, 「$A$ は $v$ を $\lambda$ 倍する」が固有値と固有ベクトルの実空間における幾何的な意味となる.
一方で $\lambda$ が実でない複素固有値の時, 対応する固有ベクトルも実ベクトルでなくなり, 「$A$ は $v$ を $\lambda$ 倍する」は複素空間における $A$ の説明となってしまう.
実正方行列が持つ複素固有値と複素固有ベクトルの意味を, どうにかして実空間上での作用として説明できないだろうか ?
結論
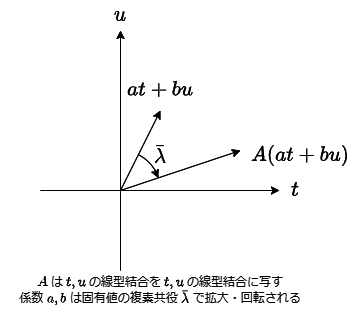
$\lambda, v$ をそれぞれ実正方行列 $A$ の固有値と対応する固有ベクトルとすると, これらは $r, \theta \in \mathbb{R}, t, u \in \mathbb{R}^d$ によってそれぞれ $\lambda = r(\cos{\theta}+i\sin{\theta}), v = t+iu$ と書くことができる ($i$ は虚数単位).
この時, $A$ は $t, u$ の線型結合を $t, u$ の線型結合に写し, $a, b \in \mathbb{R}$ に対して $A(at+bu) = a't+b'u$ となるとすると, $[a', b']^t$ はベクトル $[a, b]^t$ を $r$ 倍して $-\theta$ だけ回転させて得られる.
この説明は $\lambda, v$ が実である時にも成立する.
前提知識
- 線型代数
- 複素数
たぶん問題設定と結論が理解できる程度の知識があるなら大丈夫.
解説に現れる複素平面 (複素数と行列の対応関係) が分からなければ, 天下り的ではあるが実空間ベースでの証明も載せたので読み飛ばしてもいい.
解説
固有値, 固有ベクトル
詳細は線型代数, スペクトル理論の記事か本を参照.
複素正方行列 $A \in M(d, \mathbb{C}) \cong \mathbb{C}^{d \times d}$ に対して,
$$ Av = \lambda v, \quad \lambda \in \mathbb{C}, \ v \in \mathbb{C}^d, $$
が成り立つ時, $\lambda$ を $A$ の固有値, $v$ を ($\lambda$ に対応する) 固有ベクトルと呼ぶ.
通例では固有ベクトルは $v \neq 0$ とすることが多いが, 以降の議論は $v = 0$ を認めても成り立つためそれで通す.
実正方行列は複素行列であるとも言えるので同じく固有値, 固有ベクトルが存在し, それぞれ実数, 実ベクトルとなるとは限らないのでその時の作用について論じていく.
複素数の積の実空間上での記述
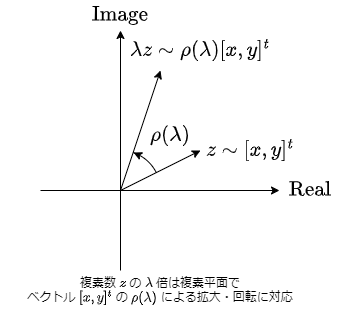
複素数の積の幾何的意味と言えば複素平面で説明される $2$ 次元ベクトルの回転である.
つまり, $z = x+iy, \lambda = \alpha+i\beta \in \mathbb{C}$ ($x, y, \alpha, \beta \in \mathbb{R}$) に対して,
$$ \lambda z = (\alpha x-\beta y)+i(\beta x+\alpha y), $$
であり, 複素数 $z$ と $2$ 次元実ベクトル $[x, y]^t$ を同一視すれば1,
$$ \lambda z \sim \begin{bmatrix} \alpha x-\beta y \\ \beta x+\alpha y \end{bmatrix} = \rho(\lambda) \begin{bmatrix} x \\ y \end{bmatrix}, \quad \rho(\lambda) := \begin{bmatrix}
\alpha & -\beta \\
\beta & \alpha \\
\end{bmatrix}, $$
と複素数の積を実行列と実ベクトルの積で記述できる.
これにより, 複素ベクトル $v = t+iu \in \mathbb{C}^d$ ($t, u \in \mathbb{R}^d$) の $\lambda$ によるスカラー倍は, 適当に転置を取れば,
$$ \lambda v = \begin{bmatrix} \lambda v_0 \\ \lambda v_1 \\ \vdots \\ \lambda v_{d-1} \end{bmatrix} \sim \begin{bmatrix} [t_0, u_0]\rho(\lambda)^t \\ [t_1, u_1]\rho(\lambda)^t \\ \vdots \\ [t_{d-1}, u_{d-1}]\rho(\lambda)^t \end{bmatrix} = [t, u]\rho(\lambda)^t, $$
と書けることになる.
よって, $d$ 次元複素ベクトルの複素スカラー倍は $d \times 2$ 実行列と $2$ 次正方行列の積と同一視できることが分かった.
実行列の複素固有ベクトルへの作用
複素ベクトル $v = t+iu \in \mathbb{C}^d$ ($t, u \in \mathbb{R}^d$) への実行列 $A \in M(d, \mathbb{R})$ の作用は, $At, Au$ が共に実ベクトルとなることから,
$$ Av = At+iAu \sim [At, Au] = A[t, u], $$
となり, $d \times 2$ 実行列 $[t, u]$ への $A$ の作用で記述されることが分かる.
従って, $\lambda \in \mathbb{C}, v \in \mathbb{C}^d$ を $A \in M(d, \mathbb{R})$ の固有値と対応する固有ベクトルとすると,
$$ A[t, u] \sim Av = \lambda v \sim [t, u]\rho(\lambda)^t, $$
となり, $z \sim [x, y]^t, z' \sim [x', y']^t$ に対して $z = z' \Leftrightarrow [x, y] = [x', y']$ が成り立つことから (演習),
$$ A[t, u] = [t, u]\rho(\lambda)^t, $$
が得られる.
これは $A$ による作用が $t, u$ で張られる空間をそれ自身に写すことを示しており, $a, b \in \mathbb{R}$ による $t, u$ の線型結合 $at+bu$ への $A$ の作用を考えると,
$$ A(at+bu) = A[t, u] \begin{bmatrix} a \\ b \end{bmatrix} = [t, u]\rho(\lambda)^t \begin{bmatrix} a \\ b \end{bmatrix}, $$
より, $[a_\lambda, b_\lambda]^t := \rho(\lambda)^t[a, b]^t$ と置けば $A$ は $t, u$ の $a, b$ による線型結合を $a_\lambda, b_\lambda$ による線型結合に写すことが分かる.
また, $\rho(\lambda)^t = \rho(\bar{\lambda})$ ($\bar{\lambda}$ は複素共役) に注意すると,
$$ a_\lambda+ib_\lambda \sim \rho(\lambda)^t \begin{bmatrix} a \\ b \end{bmatrix} \sim \bar{\lambda}(a+ib), $$
であり, $r, \theta \in \mathbb{R}$ によって $\lambda = r(\cos{\theta}+i\sin{\theta})$ と書けば $\bar{\lambda} = r(\cos{(-\theta)}+i\sin{(-\theta)})$ より, $[a_\lambda, b_\lambda]^t$ は $[a, b]^t$ を $r$ 倍して $-\theta$ だけ回転させたベクトルだと言える.
実空間ベースの直接証明
以上のことは $A$ の固有ベクトルの実部, 虚部への $A$ の作用を直接計算することでも示すことができる.
$\lambda \in \mathbb{C}$ が $A \in M(d, \mathbb{R})$ の固有値ならば $\bar{\lambda} \in \mathbb{C}$ も $A$ の固有値であり, $\lambda$ に対応する固有ベクトル $v \in \mathbb{C}^d$ に対して $\bar{v} \in \mathbb{C}^d$ は $\bar{\lambda}$ に対応する固有ベクトルとなることを用いる.
以降の議論を含めて $\lambda \in \mathbb{R}$ でも成り立つことに注意.
$\lambda = \alpha+i\beta \in \mathbb{C}$ ($\alpha, \beta \in \mathbb{R}$) を実正方行列 $A \in M(d, \mathbb{R})$ の固有値とし, $v = t+iu \in \mathbb{C}^d$ ($t, u \in \mathbb{R}^d$) を対応する固有ベクトルとする.
この時,
$$ \begin{align}
\alpha & = \frac{1}{2}(\lambda+\bar{\lambda}), & \beta & = \frac{1}{2i}(\lambda-\bar{\lambda}), \\
t & = \frac{1}{2}(v+\bar{v}), & u & = \frac{1}{2i}(v-\bar{v}), \\
\end{align} $$
と書けるので, $A$ の $t, u$ への作用はそれぞれ,
$$ \begin{align}
At & = \frac{1}{2}(\lambda v+\bar{\lambda}\bar{v}) \\
& = \frac{1}{2}((\alpha+i\beta)(t+iu)+(\alpha-i\beta)(t-iu)) \\
& = \alpha t-\beta u, \\
Au & = \frac{1}{2i}(\lambda v-\bar{\lambda}\bar{v}) \\
& = \frac{1}{2i}((\alpha+i\beta)(t+iu)-(\alpha-i\beta)(t-iu)) \\
& = \beta t+\alpha u, \\
\end{align} $$
となる.
よって,
$$ A[t, u] = [t, u]\rho(\lambda)^t, $$
が得られた.
あとは前節と同様に, $a, b \in \mathbb{R}$ による $A(at+bu)$ を考えると, $[a_\lambda, b_\lambda]^t := \rho(\lambda)^t[a, b]^t$ により,
$$ A(at+bu) = a_\lambda t+b_\lambda u, $$
となることが分かり, $\lambda = r(\cos{\theta}+i\sin{\theta})$ ($r, \theta \in \mathbb{R}$) と書くと,
$$ \rho(\lambda) = r \begin{bmatrix}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta} & \cos{\theta} \\
\end{bmatrix}, $$
でこれはベクトルを $r$ 倍して $\theta$ だけ回転させる行列なので, $[a_\lambda, b_\lambda]^t$ は $[a, b]^t$ を $r$ 倍して $-\theta$ だけ回転させたベクトルであることが示された.
実験
以上のことを Python (NumPy) で確認してみる.
正方行列の固有値, 固有ベクトルは numpy.linalg.eig で得られる.
$A(at+bu)$ を直接計算する方法と $[a_\lambda, b_\lambda]^t = \rho(\lambda)^t[a, b]^t$ で係数を計算する方法を比べて最大絶対誤差で評価する.
import numpy as np
rng = np.random.default_rng()
# 10 次実正方行列を正規乱数で 10**4 個生成して固有値, 固有ベクトルを取得
n = 10**4
d = 10
A = rng.normal(size=[n, d, d])
lmd, e = np.linalg.eig(A)
# 虚部が非ゼロの固有値と対応する固有ベクトルを選ぶ
ii = np.where(lmd.imag!=0)
j = ii[1][np.unique(ii[0], return_index=True)[1]]
l = lmd[np.arange(n), j]
v = e[np.arange(n), :, j]
# 固有ベクトルを実部と虚部に分解して線型結合の係数 a, b を正規乱数で生成
t, u = v.real, v.imag
ab = rng.normal(size=[n, 2, 1])
a, b = ab[:, 0], ab[:, 1]
# \rho(\lambda) を使って A@(a*t+b*u) = a_l*t+b_l*u となる (予定の) a_l, b_l を計算
# \rho(\lambda) を生成
def rho(lmd):
alp = np.reshape(lmd.real, np.shape(lmd)+(1, 1))
bet = np.reshape(lmd.imag, np.shape(lmd)+(1, 1))
return np.block([[alp, -bet], [bet, alp]])
# 最後の 2 axes について転置
def trans(A):
return np.transpose(A, tuple(np.arange(A.ndim-2))+(-1, -2))
ab_l = (trans(rho(l))@ab)
a_l, b_l = ab_l[:, 0], ab_l[:, 1]
# A@(a*t+b*u) = a_l*t+b_l*u の検算
# == では丸めと固有値計算の誤差で False になり得るので最大絶対誤差で評価する
print('max abs error of A(at+bu)-(a_l t+b_l u): {}'.format(np.max(np.abs((A@(a*t+b*u)[..., np.newaxis])[..., 0]-(a_l*t+b_l*u)))))
max abs error of A(at+bu)-(a_l t+b_l u): 2.1316282072803006e-14
-
代数学的には複素空間 $\mathbb{C}$ と実空間 $\mathbb{R}^2$ は同型であり, 複素数の作用について同変であると言う. ↩