はじめに
前回までのあらすじ
陰謀論にはまっているわたしは、ジョンレノンが殺される原因となった、ある周波数にたどりつきました。(諸説あり)しかし、世の中にはその周波数の音を語る偽物が横行していたのです。(妄想です)
そうであるならば、「自分でその奇跡の音を作り出すしかない」と心に誓ったのでした。
という訳で中身はpythonでの音生成のプログラミングです。
前回の記事はこちらです。
Pythonでソルフェジオ周波数のwavファイルを生成してみる①
作るもの
前回作った無機質なソルフェジオ周波数のwavファイルを少しいい感じにしていきたいと思います。
使うもの
開発環境:
・AWS cloud9
言語:
・python(2.7.14)
パッケージ:
・numpy(1.15.3)
・scipy(1.1.0)
・matplotlib
前回とほぼ変わらずですが、波形を表示するためにmatplotlibを使います。
matplotlibはpythonでグラフを描くといえば、これみたいなパッケージです。おしゃれなグラフがいいという方はseabornを追加してもらってもいいですが、わたしはこれでも満足しています。
やってみる
今回は前置き短くサクサクやっていきましょう。
波形を生成する部分を関数化する
後々さまざまな周波数の波形を作りたくなるので関数にしていきましょう。
import numpy as np
from scipy.io import wavfile
RATE = 44100
def makeSinWave(frequency,seconds):
phases = np.cumsum(2.0 * np.pi * frequency / RATE * np.ones(int(RATE * seconds)))
wave = np.sin(phases)
return wave
if __name__ == '__main__':
music = np.array([])
wave = makeSinWave(528,1)
music = np.append(music, wave)
music = (music * float(2 ** 15 - 1)).astype(np.int16)
wavfile.write("music.wav", RATE, music)
一応説明しておきますと、前回のプログラムで正弦波を生成する部分を関数にしました。引数は周波数と秒数です。あとは最初に空っぽの変数music(numpyのarray)を作っておき、あとから追加していく形にしています。
16bitに変換してwavで書き出す部分は変わりありません。
波形をグラフで見てみる
これから倍音やら和音やら色々音を変化させていこうと思うのですが、耳だけではなく目でも確認してもらおうと思います。そこで、先ほど紹介したmatplotlibを導入します。
いつものようにパッケージのインストールから始めます。
以下のコマンドをターミナルに打ち込みましょう。
$sudo pip install matplotlib
これだけで、あれよあれよと必要なものをインストールしてくれます。神に感謝です。
(もちろんプログラミングの神です)
では、コードをアップデートします。
import numpy as np
from scipy.io import wavfile
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
RATE = 44100
def makeSinWave(frequency,seconds):
phases = np.cumsum(2.0 * np.pi * frequency / RATE * np.ones(int(RATE * seconds)))
wave = np.sin(phases)
return wave
if __name__ == '__main__':
music = np.array([])
wave = makeSinWave(528,1)
music = np.append(music, wave)
music = (music * float(2 ** 15 - 1)).astype(np.int16)
wavfile.write("music.wav", RATE, music)
plt.plot(music)
plt.xlim([0,441])
plt.savefig("wave.png")
今回変更した部分は最初のimport部分と最後のグラフ描画部分です。
importの部分はcloud9でmatplotlibを使うために試行錯誤したものです。
matplotlib.use('Agg')というのはバックエンドをAggに変更しているのだそうです。これはcloud9がGUI(Xwindow)を使えないためだそうです。
最後はプロットして画像として保存しています。matplotlibの書き方には大きく二つの流派があるそうですが、シンプルにpltで済ます方法で行きます。
では出来上がったファイルを開いて波形をみてみましょう。
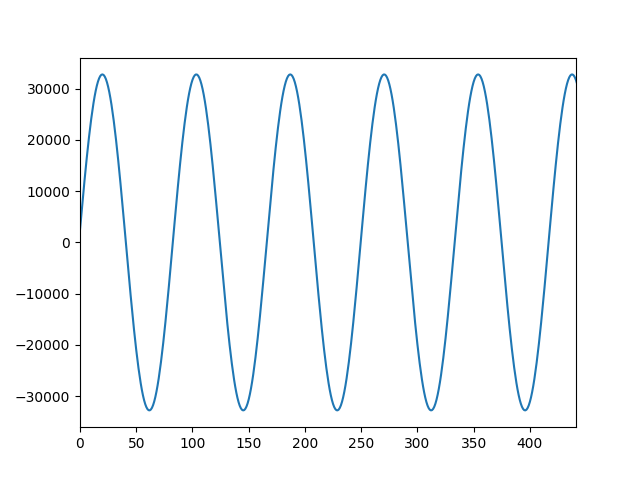
ご覧ください。これが奇跡の周波数です!
ただの正弦波ですね。
倍音を加えてみる
気を取り直して続いて行ってみましょう。音を聞いていただければ、お分かりかと思いますが非常に無機質です。NHKの時報みたいに。
それもそのはず、実際の楽器の音はこんな純粋に一つの周波数で出来てはいなのです。いくつもの周波数が重なり合って複雑な波を作り出しているのです。それが音色となって人を心を揺さぶるわけですね。
とりわけ倍音といって、基音(もとの周波数)の整数倍の周波数が多く重なりあっているそうです。
ただプログラミング的には単純です。整数倍の波を生成して加算するだけです。
早速やっていきましょう。
import numpy as np
from scipy.io import wavfile
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
RATE = 44100
def makeSinWave(frequency,seconds):
phases = np.cumsum(2.0 * np.pi * frequency / RATE * np.ones(int(RATE * seconds)))
wave = np.sin(phases)
return wave
def makeSinWaveWithOvertone(frequency,seconds):
wave = (makeSinWave(frequency,seconds) + 0.5*makeSinWave(0.5*frequency,seconds) + 0.5*makeSinWave(2.0*frequency,seconds))/2.0
return wave
if __name__ == '__main__':
music = np.array([])
wave = makeSinWaveWithOvertone(528,1)
music = np.append(music, wave)
music = (music * float(2 ** 15 - 1)).astype(np.int16)
wavfile.write("music.wav", RATE, music)
plt.plot(music)
plt.xlim([0,441])
plt.savefig("wave.png")
変更点は新たな関数makeSinWaveWithOvertoneを追加した部分です。
引数は周波数frequencyと秒数secondsです。内部では周波数が2倍の波形と2分の1の波形を加算しているだけです。倍音は大きさを半分にしています。最後に大きさを調整して出来上がりです。
波形も合わせて載せておきます。
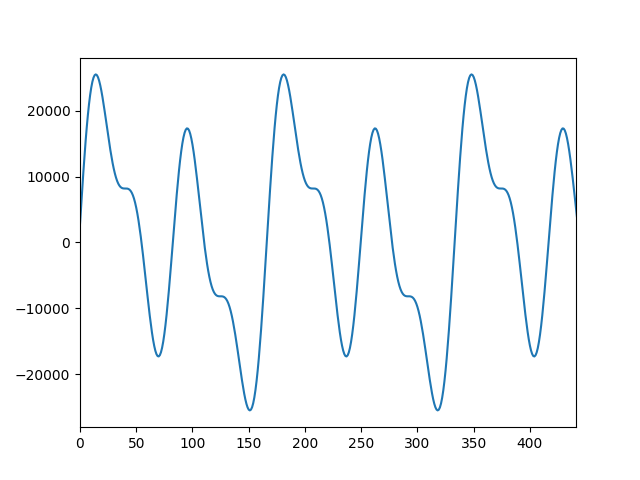
多少複雑になりました。音も少しまろやかになった感じです。
和音にしてみる
最後に和音を作ってみましょう。和音と言っても、なんのことはない単なる加算です。
そこで前回の前置きを思い出していただきたいのですが、実はソルフェジオ周波数は9つあったのでした。それぞれ効果が違うそうなのですが、折角なので全部作ってみましょう。
ちなみにそれぞれの音の周波数と効果は以下のようになっています。
| No. | 周波数 | 効果 |
|---|---|---|
| 1 | 174 Hz | 意識拡大と進化の基礎 |
| 2 | 285 Hz | 多次元領域からの意識拡大と促進 |
| 3 | 396 Hz | トラウマ・恐怖からの解放 |
| 4 | 417 Hz | 変容の促進 |
| 5 | 528 Hz | DNA の修復 |
| 6 | 639 Hz | 人間関系の修復 |
| 7 | 741 Hz | 表現力の向上 |
| 8 | 852 Hz | 直感力の覚醒 |
| 9 | 963 Hz | 高次元、宇宙意識とつながる |
No.1から凡人には理解不能ですね。No.9までいくと宇宙とつながります。いまからワクワクが止まりませんね。
ではコードを書き換えます。
ちなみに私の記事のコードはすべてコピペで動きます。変更部分だけのせるとうまく動かなかったりしますから。考えずにコピペして、まず動かしてみてください。
『考えるな、感じるんだ』(ブルース・リー)
import numpy as np
from scipy.io import wavfile
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
RATE = 44100
SOLF = [174,285,396,417,528,639,741,852,963]
def makeSinWave(frequency,seconds):
phases = np.cumsum(2.0 * np.pi * frequency / RATE * np.ones(int(RATE * seconds)))
wave = np.sin(phases)
return wave
def makeSinWaveWithOvertone(frequency,seconds):
wave = (makeSinWave(frequency,seconds) + 0.5*makeSinWave(0.5*frequency,seconds) + 0.5*makeSinWave(2.0*frequency,seconds))/2.0
return wave
if __name__ == '__main__':
music = np.array([])
w1 = makeSinWaveWithOvertone(SOLF[0],1)
w2 = makeSinWaveWithOvertone(SOLF[3],1)
w3 = makeSinWaveWithOvertone(SOLF[6],1)
wave = w1 + w2 + w3
music = np.append(music, wave)
w1 = makeSinWaveWithOvertone(SOLF[1],1)
w2 = makeSinWaveWithOvertone(SOLF[4],1)
w3 = makeSinWaveWithOvertone(SOLF[7],1)
wave = w1 + w2 + w3
music = np.append(music, wave)
w1 = makeSinWaveWithOvertone(SOLF[2],1)
w2 = makeSinWaveWithOvertone(SOLF[5],1)
w3 = makeSinWaveWithOvertone(SOLF[8],1)
wave = w1 + w2 + w3
music = np.append(music, wave)
music = (music * float(2 ** 15 - 1)).astype(np.int16)
wavfile.write("music.wav", RATE, music)
plt.plot(music)
plt.xlim([0,441])
plt.savefig("wave1.png")
plt.plot(music)
plt.xlim([RATE,RATE + 441])
plt.savefig("wave2.png")
plt.plot(music)
plt.xlim([2.0*RATE,2.0*RATE + 441])
plt.savefig("wave3.png")
そこまで説明はいらないと思いますが、一応説明しますと。
まずソルフェジオ周波数のリストを作っています。そして(No.1 No.4 No.7)と(No.2 No.5 No.8)と(No.3 No.6 No.9)の和音を1秒ずつつないでいます。
最後にそれぞれの波形をファイルに書き出します。
それぞれの波形ものせておきます。
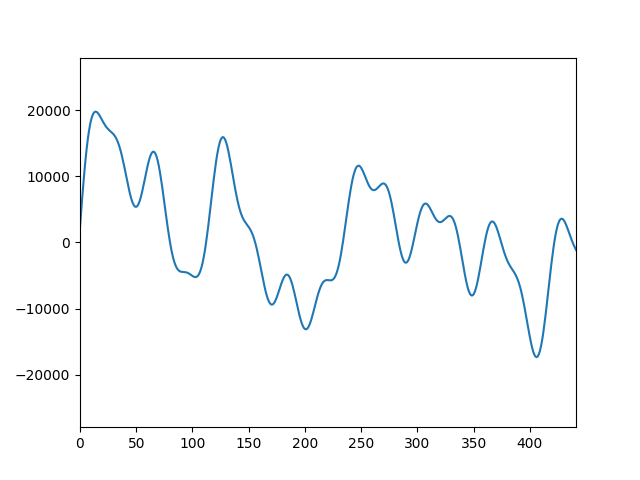
(No.1 No.4 No.7)の和音
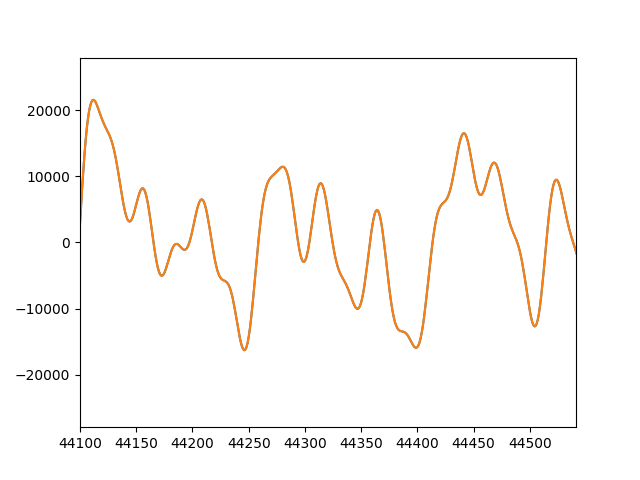
(No.2 No.5 No.8)の和音
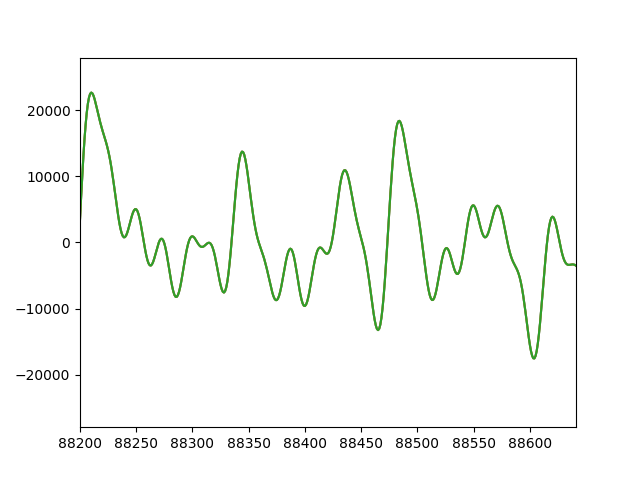
(No.3 No.6 No.9)の和音
いかがでしょうか?かなり複雑な波形になりました。音もなにやら厳かな雰囲気がでてきてると思います。これならチャクラ開きそうです。
あとは皆さま、ご自由にいろいろいじってみてください。さらにチャクラが開きそうな音が作れたら教えてください。
終わりに
前置きはさておき、pythonで波形から作ってwavファイルを生成してみました。
その昔、研究室の先輩が音を使った脳科学の実験で音をプログラミングしていて、なんか難しいことやってるなと思っていましたが、今の技術力をもってすれば一瞬でしたね。
一旦このシリーズは、これにて終了させていただきます。ちなみにソルフェジオ周波数の和音を色々みていて気付いたことがあります。それはNo.7がなんだか浮いているってことです。その他の周波数と和音を形成しにくいです。
この話はそのうち、書こうかなとも思っています。たぶん。