ガウス混合モデル（GMM）のおさらい

ガウス混合モデル

ガウス混合モデル（GMM）は、複数のガウス分布（正規分布）の組み合わせによってデータ全体の確率分布を表現する統計モデルです。このモデルは、各ガウス分布が異なる平均値（中心）と共分散（データの広がり具合）を持ち、これらの分布を利用してデータセット全体の複雑な構造を捉えます。

コンポーネント	説明
平均値（μ）	各ガウス分布の中心を示す
共分散（Σ）	分布の広がりや形状を定義し、大きいほど広がり、小さいほど集中する
混合重み（π）	各ガウス分布がデータセットに寄与する程度を示す重み。全コンポーネントの混合重みの合計は1になる

パラメータ推定

GMMのパラメータは、期待最大化（EM）アルゴリズムによって推定されます。このアルゴリズムは以下のステップで構成されます：

• 期待ステップ（Eステップ）: 現在のパラメータを使って、データポイントが各ガウス分布から生成される確率（負担率）を計算します。
• 最大化ステップ（Mステップ）: 負担率を用いて、平均値、共分散、混合重みを再計算し、パラメータを更新します。
• このEステップとMステップを繰り返すことで、モデルのパラメータがデータに最も適合するように調整されます。

実装例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture

# 5つの正規分布からデータを生成
np.random.seed(0)
n_samples = 500
means = np.array([[0, 0], [3, 3], [-3, 3], [3, -3], [-3, -3]])
covariances = np.array([[[1, 0.5], [0.5, 1]], [[1, -0.5], [-0.5, 1]], 
                        [[1, 0.5], [0.5, 1]], [[1, -0.5], [-0.5, 1]], 
                        [[1, 0.5], [0.5, 1]]])
weights = np.array([0.2, 0.3, 0.1, 0.2, 0.2])

X = np.concatenate([np.random.multivariate_normal(mean, cov, int(weight*n_samples))
                    for mean, cov, weight in zip(means, covariances, weights)])

# ガウス混合モデルをフィット
gmm = GaussianMixture(n_components=5, random_state=0)
gmm.fit(X)

# データのプロット
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], s=5, label='Data', color='blue', alpha=0.5)
# 各ガウス分布の平均をプロット
plt.scatter(gmm.means_[:, 0], gmm.means_[:, 1], marker='o', s=100, label='Means', color='red', edgecolors='black')
# 各ガウス分布の等高線をプロット
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X_grid, Y_grid = np.meshgrid(x, y)
Z = -gmm.score_samples(np.array([X_grid.ravel(), Y_grid.ravel()]).T)
Z = Z.reshape(X_grid.shape)
plt.contour(X_grid, Y_grid, Z, levels=10, linewidths=1, colors='green', linestyles='dashed', alpha=0.5)
plt.xlabel('X1')
plt.ylabel('X2')
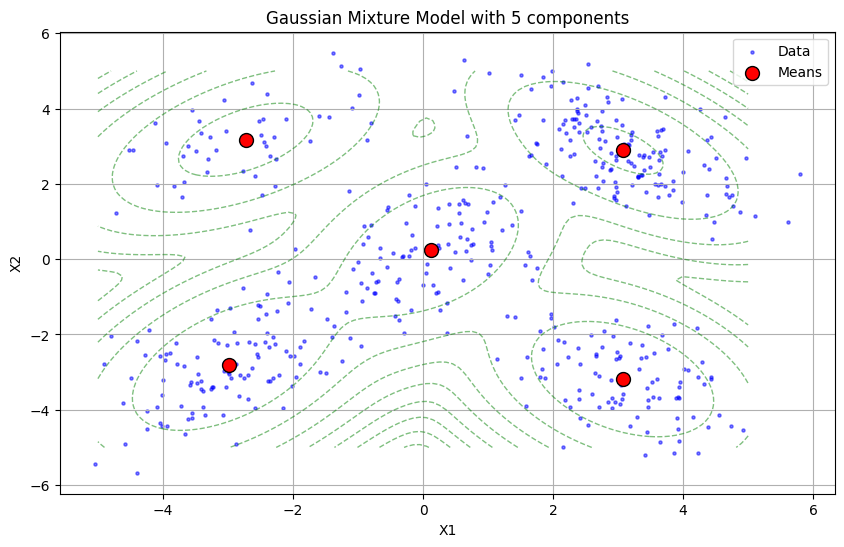
plt.title('Gaussian Mixture Model with 5 components')
plt.legend()
plt.grid(True)
plt.show()

# データのプロットとクラスタリング結果の表示
plt.figure(figsize=(14, 8))

# データのプロット
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], s=10, color='blue', alpha=0.5)
plt.title('Data')
plt.xlabel('X1')
plt.ylabel('X2')

# クラスタリング結果の表示
plt.subplot(1, 2, 2)
plt.scatter(X[:, 0], X[:, 1], s=10, color='blue', alpha=0.5)
for i in range(gmm.n_components):
    mean = gmm.means_[i]
    cov = gmm.covariances_[i]
    # ガウス分布の楕円をプロット
    v, w = np.linalg.eigh(cov)
    v = 2. * np.sqrt(2.) * np.sqrt(v)
    u = w[0] / np.linalg.norm(w[0])
    angle = np.arctan(u[1] / u[0])
    angle = 180. * angle / np.pi  # 角度を度に変換
    ell = plt.matplotlib.patches.Ellipse(mean, v[0], v[1], 180. + angle, color='red')
    ell.set_clip_box(plt.gca().bbox)
    ell.set_alpha(0.5)
    plt.gca().add_artist(ell)
    # 各データポイントの所属するクラスタを色分けして表示
    plt.scatter(X[gmm.predict(X) == i][:, 0], X[gmm.predict(X) == i][:, 1], s=10, color=plt.cm.tab10(i), alpha=0.5)
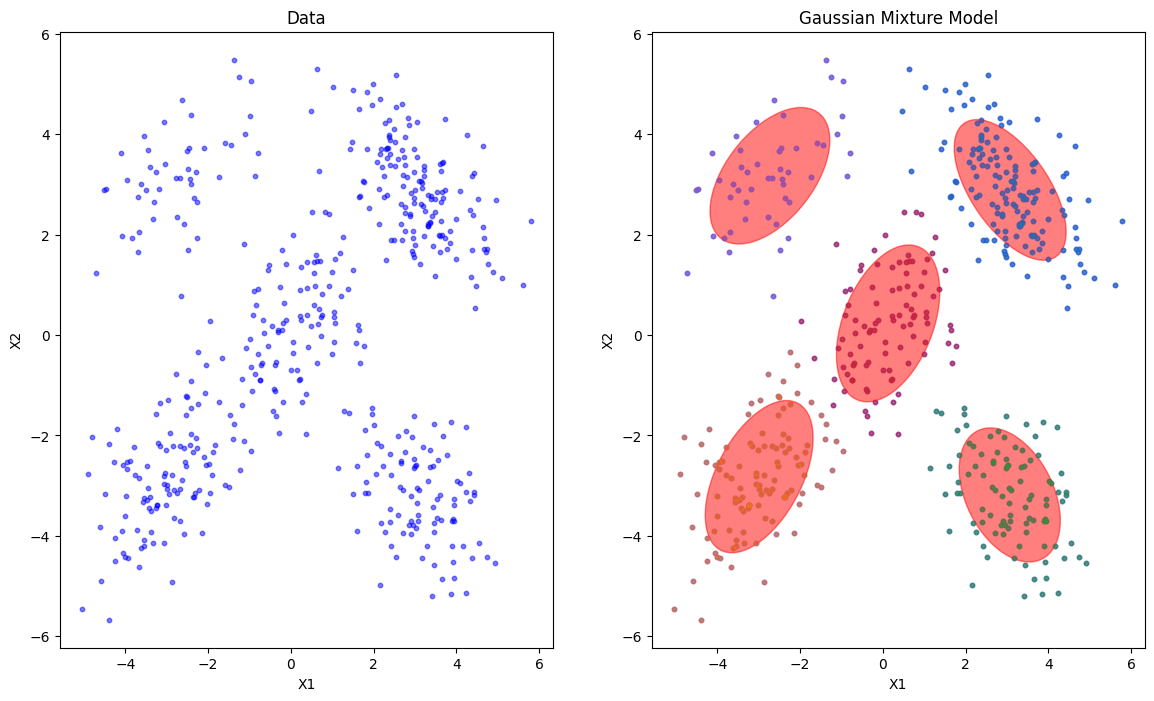
plt.title('Gaussian Mixture Model')
plt.xlabel('X1')
plt.ylabel('X2')

plt.show()

ガウス混合モデル（GMM）はどういう時に使用する？

他の手法と比較してみましょう。

モデル名	適用場面
ガウス混合モデル (GMM)	複数の確率分布から生成されたデータのモデリングや複雑なデータ分布のモデリング、異常検知などの場合
K-means クラスタリング	単純なクラスタリング問題やクラスタ数が明確な場合、計算量を抑えたい場合
DBSCAN	密度に基づいたクラスタリングやクラスタの形状が不規則な場合
t-SNE	高次元データの可視化や非線形な構造を持つデータをマッピングする場合
階層的クラスタリング	クラスタの階層構造を理解したい場合やクラスタ数が事前に不明確な場合
ニューラルネットワーク	複雑な非線形関係をモデル化する必要がある場合や大規模なデータセットに対処する場合

複数の確率分布 が含まれるか否かをデータからどう判断する？

EDAでデータ概観をつかみます。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.mixture import GaussianMixture
from scipy.stats import norm

# サンプルデータの生成
np.random.seed(0)
data = np.concatenate([np.random.normal(loc=0, scale=1, size=1000), 
                       np.random.normal(loc=5, scale=1.5, size=1000)])

# BICを用いて最適な成分数を探索
bic_values = []
max_components = 10
for n_components in range(1, max_components + 1):
    gmm = GaussianMixture(n_components=n_components)
    gmm.fit(data.reshape(-1, 1))
    bic_values.append(gmm.bic(data.reshape(-1, 1)))

# BIC値のプロット
plt.figure(figsize=(10, 6))
plt.plot(range(1, max_components + 1), bic_values, marker='o', linestyle='-')
plt.title("BIC Values for Different Number of Components")
plt.xlabel("Number of Components")
plt.ylabel("BIC Value")
plt.xticks(range(1, max_components + 1))
plt.grid(True)
plt.show()

# 最適な成分数の選択
optimal_components = np.argmin(bic_values) + 1
print("最適な成分数:", optimal_components)

# ガウス混合モデル (GMM) のフィット
gmm = GaussianMixture(n_components=optimal_components)
gmm.fit(data.reshape(-1, 1))
pdf = np.exp(gmm.score_samples(np.linspace(data.min(), data.max(), 1000)[:, np.newaxis]))

plt.figure(figsize=(10, 6))
plt.hist(data, bins=30, density=True, alpha=0.5)
plt.plot(np.linspace(data.min(), data.max(), 1000), pdf, color='red', linewidth=2)
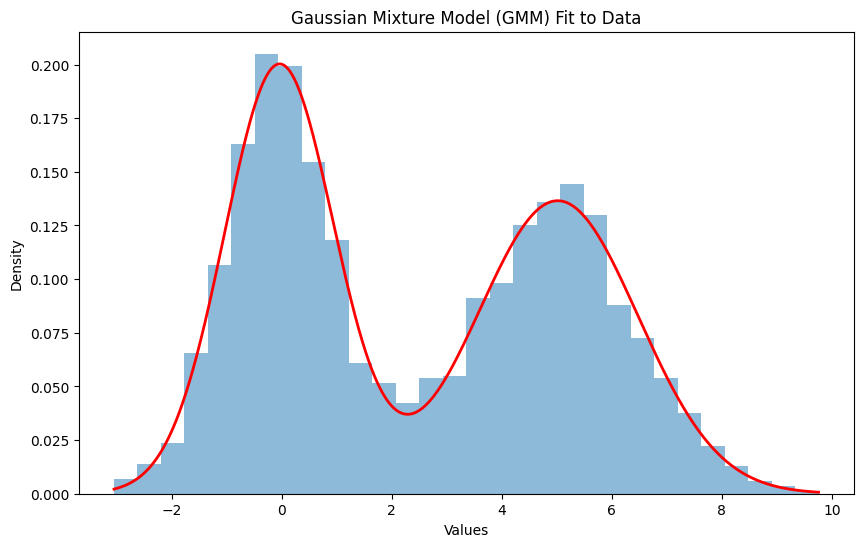
plt.title("Gaussian Mixture Model (GMM) Fit to Data")
plt.xlabel("Values")
plt.ylabel("Density")
plt.show()

# 尤度比検定
log_likelihood_single = np.sum(norm.logpdf(data, loc=np.mean(data), scale=np.std(data)))
log_likelihood_gmm = np.sum(gmm.score(data.reshape(-1, 1)))
likelihood_ratio = -2 * (log_likelihood_single - log_likelihood_gmm)

print("尤度比検定の統計量:", likelihood_ratio)

# 判定
if likelihood_ratio > 3.84:  # カイ二乗分布の上側5%点（自由度1の場合）
    print("複数の確率分布がデータをよく説明している可能性が高いです。")
else:
    print("単一の確率分布でデータを説明する方が適切かもしれません。")

出力結果

尤度比検定の統計量: 9819.341557729025
複数の確率分布がデータをよく説明している可能性が高いです。