はじめに
不確実性下の意思決定理論を学びます。
スライドまとめ
不確実性下の意思決定とは
- 意思決定理論は「よりよい意思決定」を追究する学問領域
- 意思決定の定義：ある状況下で複数の選択肢から1つを選ぶこと
- 数学的表現：
- 状況 $x=(x_1,x_2,\ldots,x_N)$、選択肢 $y=(y_1,y_2,\ldots,y_M)$
- 意思決定の結果：$c_{ij}=f(x_i,y_j)$
- 不確実性下の意思決定：状況が確率的にしか判断できない場合の問題
- 理論的アプローチ：結果 $c_{ij}$ の期待値最大化を考える
意思決定と情報量
- 情報量は意思決定の精度向上に重要
- 情報量の定義：「不確実性の減少量」
- 情報エントロピー（H）を用いた不確実性の数値化：
- $H(x)=-\sum_{i=1}^N P(x_i)\log_2P(x_i)$
- 具体例：
- 2つの状況（N=2）で最大不確実性：$H(x)=1$
- 新情報により確率更新（50%→75%）：$H(x)\approx0.81$
- 情報量：$1-0.81=0.19$ bit
- 情報量がゼロの情報も存在（何も言っていない文章など）
情報の価値
- 定義：情報使用/不使用時の結果の期待値の差異
- 情報の価値の3ステップ：
- 情報による行動の変化
- 行動変化による結果の変化
- 変化前後の結果の差異
- 行動変容を引き起こさない情報に価値はない
- 「分からない」という情報にも価値がある場合がある
- 情報取得のコストを考慮する必要性
意思決定の実践
- 意思決定パラメータ数の削減が重要
- パラメータ削減の3つの方法：
- 変数の独立性評価
- 変数の不確実性評価
- 意思決定の階層化
- 人間が議論する場合、パラメータ数は3つ以内が理想的
- KPIツリーの活用：
- KGIの設定とKPIツリーへの分解
- 変数間の独立性/従属性の整理
- 従属性の高い変数の統合
- 不確実性の高いパラメータの優先的選択
- 意思決定プロセスの適切な粒度での分割・委譲
- 例：プロダクトチーム vs. 経営企画チーム
意思決定とセンスメイキング
- 規範的アプローチ：
- 数学的論理に基づく客観的な最適解を追求
- 公理的ルールと数学的論理を使用
- 現実社会の意思決定：
- 人々は必ずしも数学的に最適な選択をしない（行動経済学の知見）
- 合理性は主観的で、人によって異なる
- 集団における意思決定の難しさ：
- 様々な考え（合理性）を持つ人々の存在
- 政策決定などの社会全体に影響を与える意思決定
- センスメイキングの重要性：
- 意思決定（decision making）に加えて
- 人々が意思決定に納得するプロセス（sense making）も考慮
まとめ
- 不確実性下の意思決定理論：不確かな状況下でのよりよい意思決定のための科学的アプローチ
- 情報量：不確実性の減少量を表す指標
- 情報の価値：行動変容と意思決定結果の変化に基づく
- 実践的アプローチ：
- 意思決定パラメータの削減
- 変数の独立性・不確実性評価
- 意思決定プロセスの分割・委譲
- 合理性の主観性：個人や集団によって異なる
- 集団意思決定におけるセンスメイキングの重要性
Appendix
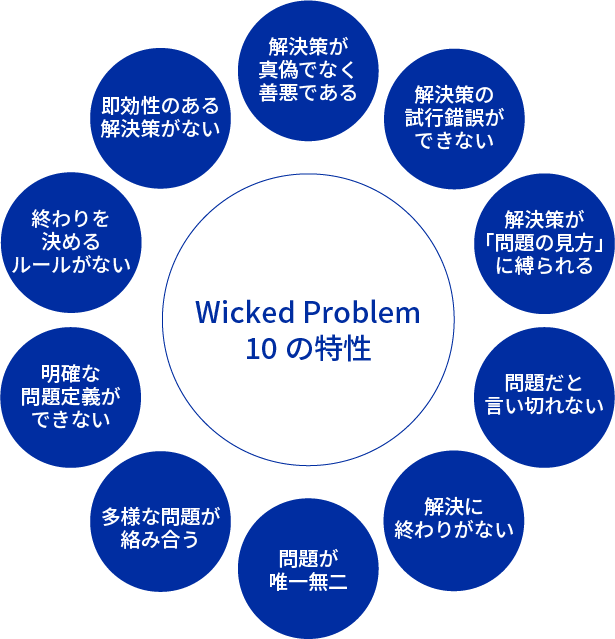
Wicked problem
Wicked problemとは、複雑で定義が困難な社会的または文化的な問題のことを指す。この概念は1970年代にHorst Rittelとmelvin Webberによって提唱さた。
典型的なWicked problemの例としては、気候変動、貧困、教育改革、都市計画など。
Wicked problemの主な特徴は以下の通り。
- 明確な定義が難しい
- 完全な解決策がない
- 解決策は「正解」または「不正解」ではなく、「より良い」または「より悪い」と評価される
- 問題の理解と解決策が相互に依存している
- 一回限りの解決策では対処できない
- 多くのステークホルダーが関与し、それぞれ異なる価値観や目標を持っている
- 他の問題と密接に関連している
典型的なWicked problemの例としては、気候変動、貧困、教育改革、都市計画などが挙げられます。
