なんですか？ 『写像』って。

はじめに

• 「写像」ってなんですか？
• 「ロジスティック写像」ってなんですか？
• 「カップルド・ロジスティック写像」ってなんですか？

写像

写像（Map）は、数学における概念の一つで、「ある集合の要素を別の集合の要素に対応づけるルールのこと」を指します。写像は、関数（Function）とも呼ばれます。

写像 $f: X \to Y$ は、集合 $X$ の各要素 $x$ に、集合 $Y$ の要素 $y$ を対応づけるルールです。
$X$ を定義域（Domain）、$Y$ を 値域（Codomain） と呼びます。
また、$x$ に対応づけられる $Y$ の要素 $y$ を $f(x)$ と表記し、$x$の 像（Image） と呼びます。

写像の種類

写像には、以下のような種類があります。

単射（Injection）：

異なる要素が常に異なる要素に写像される写像。 $$\forall x_1, x_2 \in X, x_1 \neq x_2 \Rightarrow f(x_1) \neq f(x_2)$$

全射（Surjection）：

値域の全ての要素が、定義域の少なくとも1つの要素から写像される写像。 $$\forall y \in Y, \exists x \in X, f(x) = y$$

全単射（Bijection）：

単射かつ全射である写像。全単射は、定義域と値域の要素が1対1に対応づけられる。

恒等写像（Identity Map）：

各要素を自分自身に写像する写像。 $$\forall x \in X, f(x) = x$$

ロジスティック写像

ロジスティック写像は、実数からそれ自身への写像の一種で、以下の式で定義されます。
$$f(x) = rx(1-x)$$
ここで、$r$ は正の実数であるパラメータ、$x$ は $0$ から $1$ の間の実数です。

写像は、力学系の研究において重要な役割を果たします。離散時間の力学系は、写像の反復によって記述されます。例えば、ロジスティック写像を反復的に適用することで、個体群動態などの現象をモデル化することができます。

応用例

ロジスティック写像は、生態学や人口動態の分野で広く用いられるモデルの一つです。この写像は、単一の種の個体群の時間発展を記述します。パラメータ $r$ は、個体群の成長率を表します。

ロジスティック写像の反復は、以下のように表されます。
$$x_{n+1} = f(x_n) = rx_n(1-x_n)$$
ここで、$x_n$ は時刻 $n$ における個体群の密度を表します。

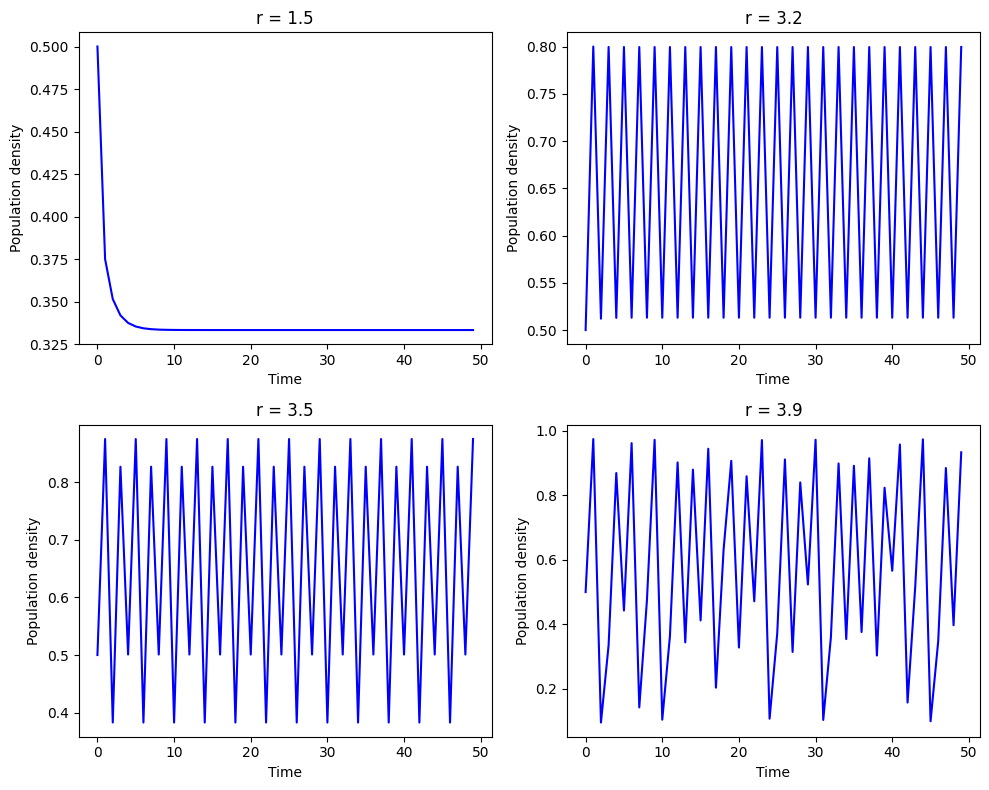
ロジスティック写像の振る舞いは、パラメータ $r$ の値によって大きく異なります。

$0 < r \leq 1$：個体群は時間とともに減少し、最終的に絶滅します。
$1 < r \leq 3$：個体群は一定の値に収束します（安定な平衡点）。
$3 < r \leq 3.57$：個体群は周期的な振動を示します（周期倍分岐）。
$3.57 < r \leq 4$：個体群はカオス的な振る舞いを示します。

以下は、ロジスティック写像の反復をPythonで実装し、個体群の時間発展をグラフ化した例です。

import numpy as np  # NumPyライブラリのインポート。数値計算を行う際に使用。
import matplotlib.pyplot as plt  # Matplotlibのpyplotモジュールのインポート。グラフを描画するために使用。

def logistic_map(r, x0, n):
    # ロジスティックマップ関数の定義。rは成長率、x0は初期集団密度、nは時間ステップ数。
    x = np.zeros(n)  # n個の要素を持つゼロ配列を作成。これが集団密度を格納する配列。
    x[0] = x0  # 配列の最初の要素に初期値を設定。
    for i in range(1, n):  # 時間が進むにつれて集団密度を計算するループ。
        x[i] = r * x[i-1] * (1 - x[i-1])  # ロジスティック方程式。次の集団密度を計算。
    return x  # 計算された集団密度の配列を返す。

r_values = [1.5, 3.2, 3.5, 3.9]  # 成長率の値のリスト。これらの値でグラフを描画。
x0 = 0.5  # 初期集団密度。
n = 50  # 時間ステップ数。

fig, axs = plt.subplots(2, 2, figsize=(10, 8))  # サブプロットを含む図の作成。2x2のグリッドで。
axs = axs.flatten()  # サブプロット配列を1次元配列に変換。

for i, r in enumerate(r_values):  # 成長率の値ごとにループ。
    x = logistic_map(r, x0, n)  # ロジスティックマップ関数を呼び出して集団密度を計算。
    axs[i].plot(range(n), x, 'b-')  # 集団密度のグラフを描画。'b-'は青色の実線で表示。
    axs[i].set_title(f'r = {r}')  # サブプロットのタイトルを設定。成長率を表示。
    axs[i].set_xlabel('Time')  # x軸のラベルを設定。
    axs[i].set_ylabel('Population density')  # y軸のラベルを設定。

plt.tight_layout()  # サブプロット間の適切な間隔を自動的に調整。
plt.show()  # 図を表示。

各サブプロットは、選択された成長率 r に対する人口密度の時間経過による変動を示しています。このモデルでは、r の値によってシステムの動的な挙動が大きく変わり、定常状態、周期的挙動、カオス的挙動など、多様なダイナミクスが生じます。特に、r = 3.9 ではカオス的な挙動が見られ、小さな初期条件の違いが時間とともに大きな差異を生じさせることが分かります。

カップルド・ロジスティック写像

カップルド・ロジスティック写像（Coupled Logistic Map）は、2つ以上の相互作用するロジスティック写像から成る非線形力学系モデルです。このモデルは、生態学、経済学、物理学などの様々な分野で、複雑な相互作用を伴うシステムの振る舞いを研究するために用いられます。

単一のロジスティック写像は、以下の式で表されます：

$$x_{n+1} = rx_n(1-x_n)$$

カップルド・ロジスティック写像では、複数のロジスティック写像が相互作用します。最も単純な場合として、2つのロジスティック写像が結合された系を考えましょう：

$$x_{n+1} = r_1x_n(1-x_n) + \epsilon(y_n - x_n)$$
$$y_{n+1} = r_2y_n(1-y_n) + \epsilon(x_n - y_n)$$

ここで、$x_n$と$y_n$は2つの状態変数、$r_1$と$r_2$はそれぞれのロジスティック写像のパラメータ、$\epsilon$は結合の強さを表すパラメータです。

カップルド・ロジスティック写像の振る舞いは、パラメータ$r_1$、$r_2$、$\epsilon$の値によって大きく異なります。結合が弱い場合（$\epsilon$が小さい場合）、2つの写像は独立に振る舞います。一方、結合が強い場合（$\epsilon$が大きい場合）、2つの写像は同期したり、複雑な相互作用を示したりします。

特徴

カップルド・ロジスティック写像は、以下のような特徴を持っています：

• カオスと秩序の共存：パラメータの値によっては、カオス的な振る舞いと規則的な振る舞いが同時に観察されることがあります。
• 同期現象：結合が強い場合、2つの写像が同期して同じ振る舞いを示すことがあります。
• 間欠的カオス：カオス的な振る舞いと規則的な振る舞いが間欠的に切り替わる現象が観察されることがあります。

応用例

カップルド・ロジスティック写像は、複雑なシステムにおける相互作用や同期現象を理解するための基本的なモデルとして使用されています。

分野	応用例
生態学	- 2つの種が相互作用する個体群動態のモデル化 - 捕食者-被食者の関係や、共生関係にある種の個体数の時間発展の解析
経済学	- 2つの市場や企業の相互作用のモデル化 - 市場の同期現象や、経済変動の解析
神経科学	- ニューロンの発火パターンの同期現象のモデル化 - 脳内の情報処理メカニズムの解明
気象学	- 大気や海洋における循環パターンの解析 - エルニーニョ現象など、気候システムの変動の理解
社会学	- 2つの集団の意見や行動の相互影響のモデル化 - 社会的な同調現象や、集団の分極化の解析
情報通信工学	- 通信ネットワークにおける同期現象の解析 - ネットワークの安定性や、情報の伝播特性の評価
機械学習	- ニューラルネットワークにおける情報処理の解析 - 複数の層や neuron 間の相互作用のモデル化

例

脳内の情報処理メカニズムの解明に、カップルド・ロジスティック写像を応用した例を以下に示します。この例では、2つの神経細胞（ニューロン）の発火パターンの同期現象をモデル化します。膜電位が閾値（threshold）を超えた場合、ニューロンが発火（スパイク）したとみなします。

import numpy as np  # NumPyライブラリをインポート。数値計算に使用
import matplotlib.pyplot as plt  # Matplotlibのpyplotモジュールをインポート。グラフ描画に使用

def coupled_logistic_neurons(r1, r2, eps, x0, y0, n, threshold):
    # カップリングされたロジスティックニューロンモデルの関数。r1とr2はニューロンの成長率、epsは相互作用の強度、
    # x0とy0は初期値、nは時間ステップ数、thresholdはスパイク閾値
    x = np.zeros(n)  # ニューロン1のメンブレンポテンシャルを格納する配列
    y = np.zeros(n)  # ニューロン2のメンブレンポテンシャルを格納する配列
    x[0], y[0] = x0, y0  # 初期値を設定。
    spike_x = np.zeros(n)  # ニューロン1のスパイク活動を記録する配列
    spike_y = np.zeros(n)  # ニューロン2のスパイク活動を記録する配列
    
    for i in range(1, n):  # 各時間ステップでニューロンの状態を更新。
        # カップリングされたロジスティックマップに基づいて次のメンブレンポテンシャルを計算
        x[i] = r1 * x[i-1] * (1 - x[i-1]) + eps * (y[i-1] - x[i-1])
        y[i] = r2 * y[i-1] * (1 - y[i-1]) + eps * (x[i-1] - y[i-1])
        
        # メンブレンポテンシャルが閾値を超えたらスパイクとして記録
        if x[i] > threshold:
            spike_x[i] = 1
        if y[i] > threshold:
            spike_y[i] = 1
    
    return x, y, spike_x, spike_y  # 計算結果を返す

r1, r2 = 3.8, 3.5  # ニューロンの成長率
eps_values = [0.1, 0.5]  # 相互作用の強度の値のリスト
x0, y0 = 0.4, 0.2  # 初期メンブレンポテンシャル
n = 1000  # 時間ステップ数
threshold = 0.7  # スパイクの閾値

fig, axs = plt.subplots(2, 2, figsize=(12, 8))  # サブプロットを含む図の作成

for i, eps in enumerate(eps_values):  # 相互作用の強度ごとにループ
    x, y, spike_x, spike_y = coupled_logistic_neurons(r1, r2, eps, x0, y0, n, threshold)  # モデルを実行
    
    # メンブレンポテンシャルのグラフをプロット
    axs[i, 0].plot(range(n), x, 'b-', label='Neuron 1')
    axs[i, 0].plot(range(n), y, 'r-', label='Neuron 2')
    axs[i, 0].set_title(f'ε = {eps}')  # サブプロットのタイトルを設定
    axs[i, 0].set_xlabel('Time')  # x軸のラベルを設定
    axs[i, 0].set_ylabel('Membrane potential')  # y軸のラベルを設定
    axs[i, 0].legend()  # 凡例を表示
    
    # スパイク活動のグラフをプロット。
    axs[i, 1].plot(range(n), spike_x, 'b-', label='Neuron 1')
    axs[i, 1].plot(range(n), spike_y, 'r-', label='Neuron 2')
    axs[i, 1].set_title(f'ε = {eps}')  # サブプロットのタイトルを設定
    axs[i, 1].set_xlabel('Time')  # x軸のラベルを設定
    axs[i, 1].set_ylabel('Spike')  # y軸のラベルを設定
    axs[i, 1].legend()  # 凡例を表示

plt.tight_layout()  # サブプロット間の適切な間隔を自動的に調整
plt.show()  # 図を表示

結合強度 $\epsilon$ が小さい場合（$\epsilon = 0.1$）、2つのニューロンの膜電位は独立に振る舞い、発火パターンに同期は見られません。一方、結合強度が大きい場合（$\epsilon = 0.5$）、2つのニューロンの膜電位は同期し、発火パターンにも同期が見られます。

まとめ

カップルド・ロジスティック写像を用いることで、脳内のニューロン間の相互作用と発火パターンの同期現象をモデル化し、情報処理メカニズムの理解に役立てることができます。

ただし、これは非常に単純化されたモデルであり、実際の脳の情報処理メカニズムを完全に説明するものではありません。
実際の脳では、多数のニューロンが複雑なネットワークを形成しており、このような同期現象が情報処理に重要な役割を果たしていると考えられています。より現実的なモデルを構築するためには、ニューロンの生理学的特性や、シナプス結合の詳細なダイナミクスなどを考慮する必要があります。

さいごに

「写像」「ロジスティック写像」「カップルド・ロジスティック写像」について順に見ていきました。写像っていいものですね。