はじめに
OpenCV Advent Calendar 2018の21日目の投稿です.
この記事では,代表的なエッジ保存平滑化フィルタであるバイラテラルフィルタをいかに高速化するかについて書いています.
バイラテラルフィルタは,処理が重いフィルタとよくいわれます.
しかし,実装次第では,世間一般に言われるほど遅いフィルタではないです(と思ってます).
この記事では,それを示すために,ナイーブアルゴリズム(ちょっと近似をしますが)のままで,つまり高速化アルゴリズムを適用しないで,高速化していきます.
(正直,OpenCV成分は薄いですw)
記載している内容のほとんどは,下記の論文にあります.
また,このコードもgithubにて公開していますので,気になる方は参照ください.
Y. Maeda, N. Fukushima, and H. Matsuo, "Effective Implementation of Edge-Preserving Filtering on CPU Microarchitectures," Applied Sciences, vol. 8, no. 10, July 2018. Web
github: yoshihiromaed/FastImplementation-BilateralFilter
バイラテラルフィルタ
エッジ保存平滑化フィルタとは,輪郭などの大きなエッジを保持しつつ,平滑化を行うフィルタです.
バイラテラルフィルタは,そのエッジ保存平滑化フィルタの一つであり,FIRフィルタとして表現されます.
FIRフィルタの定義は,次式です.
\boldsymbol{\bar{I}}(\boldsymbol{p}) = \frac{1}{\eta} \sum_{\boldsymbol{q}\in \mathcal{N}(\boldsymbol{p})} f(\boldsymbol{p},\boldsymbol{q})\boldsymbol{I}(\boldsymbol{q})\\
\eta = \sum_{\boldsymbol{q}\in \mathcal{N}(\boldsymbol{p})}f(\boldsymbol{p},\boldsymbol{q})\\
\boldsymbol{\bar{I}}: 出力画像,\boldsymbol{I}: 入力画像,\boldsymbol{p}:注目画素,\boldsymbol{q}:参照画素,\\
f(\boldsymbol{p},\boldsymbol{q}): 重み関数,\mathcal{N}(\boldsymbol{p}): 参照画素の集合
この式の重み関数$f(\boldsymbol{p}, \boldsymbol{q})$を変えることで,ガウシアンフィルタなどの様々なフィルタを実現できます.
そして,バイラテラルフィルタの重み関数は次のようになります.
f(\boldsymbol{p}, \boldsymbol{q}) = \exp(\frac{\|\boldsymbol{p}-\boldsymbol{q}\|^2_2}{-2\sigma_s^2})\exp(\frac{\|\boldsymbol{I}(\boldsymbol{p})-\boldsymbol{I}(\boldsymbol{q})\|^2_2}{-2\sigma_r^2})\\
\sigma_s: 空間の平滑化係数,\sigma_r: 色の平滑化係数,\\
\|\cdot\|_2: L2ノルム
この重み関数は,最初の$\exp$の項は空間の距離に基づくガウシアン重み(通常のガウシアンフィルタと同じ),次の$\exp$の項は色空間上の距離に基づくガウシアン重みになります.
バイラテラルフィルタでは,二つ目の$\exp$の項による色空間上での距離に基づく重みによって,色が近い画素同士では重みが大きくなり,エッジを跨いだような色が遠い画素同士では重みが小さくなります.
これによって,大きなエッジを残しながら平滑化を実現しています.
OpenCVにおけるバイラテラルフィルタの実装
OpenCVにおけるバイラテラルフィルタの重み関数は,先ほどのアルゴリズムとは少し違います(正しくないです).
次式が,OpenCVにおけるバイラテラルフィルタの重み関数になります.
f(\boldsymbol{p},\boldsymbol{q}) =
EXP_s[\boldsymbol{p}-\boldsymbol{q}] EXP_r[|\boldsymbol{I}(\boldsymbol{p})_r-\boldsymbol{I}(\boldsymbol{q})_r| + |\boldsymbol{I}(\boldsymbol{p})_g-\boldsymbol{I}(\boldsymbol{q})_g| + |\boldsymbol{I}(\boldsymbol{p})_b-\boldsymbol{I}(\boldsymbol{q})_b|]\\
EXP_s[\boldsymbol{x}] = \exp(\frac{\|\boldsymbol{x}\|^2_2}{-2\sigma_s^2})\\
EXP_r[x] = \exp(\frac{x^2}{-2\sigma_r^2})
$EXP_s$と$EXP_r$はLUTを参照することを表しており,それぞれ空間の重み,色空間の重みのLUTです.
また$\boldsymbol{I}(\cdot)_r$,$\boldsymbol{I}(\cdot)_g$,$\boldsymbol{I}(\cdot)_b$は,RGBそれぞれの画素値を表しています.
通常,OpenCVでは特にコンパイル時もしくはコードで明示的に指定しなければ,Intel Integrated Performance Primitives (Intel IPP)のバイラテラルフィルタ関数を呼び出しています.
おそらく,出力からみて,OpenCVでの実装とIntel IPPはおそらく同じ計算をしていると思います(IPPでは最適化がされてはいますが).
バイラテラルフィルタの高速化
非正規化数抑制による高速化
非正規化数とバイラテラルフィルタ
唐突にでてきた非正規化数ですが,これは浮動小数点型数の特殊数の一つです(他の特殊数は,NaN,Zero,Infinityです).
IEEE754の浮動小数点型数における通常の数(正規化数)のフォーマットは次式になります.
(-1)^{sign} \times 2^{exponent-bias} \times 1.fraction\\
sign: 符号ビット,exponent: 指数部,fraction: 仮数部
それに対して,非正規化数のフォーマットは,次式です.
(-1)^{sign} \times 2^{1-bias} \times 0.fraction
正規化数と非正規化数の違いですが,$exponent$が1と見なされている点(実際はこのとき$exponent$は0で,フラグのような役割をしています),$fraction$の部分が1.で始まるか0.で始まるかの点です.
この違いによって,非正規化数は正規化数よりもより小さな値を表現することが可能です.
float型における正規化数の表現範囲(絶対値)は,$1.17549435 \times 10^{-38} ~ 3.402823466 \times 10^{38}$で,非正規化数では$1.40129846 \times 10^{-45} ~ 1.17549421 \times 10^{-38}$です.
この非正規化数ですが,より小さな値を表現できる反面,処理が非常に遅いという特徴があります.
そして,この非正規化数はバイラテラルフィルタで頻繁に発生しています.
この図は,入力画像とバイラテラルフィルタをかけたときの非正規化数の発生状況をヒートマップにしたものです.
バイラテラルフィルタの特徴として,エッジを跨いだような画素では重みが小さくなります.
このとき,非正規化数が発生しており,処理が遅くなっています.
つまり,非正規化数を発生させないようすることで高速化が見込めます.
あと,非正規化数は非常に小さな値であるため,出力結果への影響はほとんどなく,発生しないようにしても精度に影響は全くないといってもいいぐらいです.
非正規化数の抑制方法
ここでは,二つのパターンにおける非正規化数の抑制を考えます.
基本的なアプローチとしては,$\exp$関数の戻り値で非正規化数が発生しないように,次式を満たすような引数を決めればいいです.
\exp(x) > 非正規化数の最大値\
この式は,次の式と同じでこれを満たせばよいのです.
\exp(x) \ge 正規化数の最小値\\
x \ge \ln(正規化数の最小値)
なお,$\ln(正規化数の最小値)$はfloat型の場合,おおよそ-83です.
これを満たすように実装した場合,重み関数は次のようになります.
f(\boldsymbol{p},\boldsymbol{q}) = \exp(\max(\frac{\|\boldsymbol{p}-\boldsymbol{q}\|^2_2}{-2\sigma_s^2}+\frac{\|\boldsymbol{I}(\boldsymbol{p})-\boldsymbol{I}(\boldsymbol{q})\|^2_2}{-2\sigma_r^2}, \ln(正規化数の最小値))).
ただ,空間の重みは,パラメータが決まれば固定であるため,LUTを参照する場合があります.
むしろ,演算が減らせるのでそっちの方が速い可能性が高いです.
その場合,このアプローチに加えて,もう一つ考えることがあります.$\exp$の項同士の乗算による非正規化数発生の可能性です.
これには,なんらかの大きな数を乗算することによって,正規化数に変えてやるような対処をします.
つまり,次のような式になります.
f(\boldsymbol{p},\boldsymbol{q}) = o \times \exp(\max(\frac{\|\boldsymbol{p}-\boldsymbol{q}\|^2_2}{-2\sigma_s^2}, \ln(正規化数の最小値)))\exp(\max(\frac{\|\boldsymbol{I}(\boldsymbol{p})-\boldsymbol{I}(\boldsymbol{q})\|^2_2}{-2\sigma_r^2}, \ln(正規化数の最小値)))\\
$o$がなんらかしらの大きな数です.
この$o$ですが,大きすぎると処理の途中にオーバーフローしてしまう可能性があり,FIRフィルタの定義式とバイラテラルフィルタの重みの最大値は1であることより次の値にすればよいことが分かります.
なお,この値は画素値の最大値が255であるとした場合です.
o = \frac{正規化数の最大値}{255|\mathcal{N}(\boldsymbol{p})|}
しかし,これでもまだ問題があります.$o$を乗算してもまだ非正規化数である可能性です.
これはパラメータによっては(平滑化係数が小さい場合),これでも非正規化数であるような小さな値であることがあります.
その場合は,各項の最小値と$o$との乗算結果が非正規化数にならないように,各項の有効桁数を減らすことで対処します.
これは,$\ln(正規化数の最小値)$の部分を$\ln(乗算しても非正規化数にならない最小値)$に変更することで実現できます.
ちなみに,これらのアプローチはmax演算や乗算が増えたりしますが,それよりも非正規化数が発生しないことによる恩恵の方が大きいため,無視できるぐらいのコストになります.
実装方法
実装方法として,重み関数を1項もしくは複数項として処理するか,LUTを使用するか等の様々な組み合わせが考えられますが,ここでは最も速かった実装を紹介します(他の実装は,githubを参照してください,大体の考えられるパターンの実装があります).
最も速かった実装とは,空間重みと色重みの両方でLUTを使用し,色重みだけ量子化して近似することでLUTサイズを小さくする実装です.
その実装は,式としては次のようになります.
f(\boldsymbol{p},\boldsymbol{q}) = EXP_s[\boldsymbol{p}-\boldsymbol{q}]EXP_{rq}[\lfloor\phi(\|\boldsymbol{I}(\boldsymbol{p})-\boldsymbol{I}(\boldsymbol{q})\|^2_2) \rfloor],\\
EXP_s[\boldsymbol{x}] = \exp(\frac{\|\boldsymbol{x}\|^2_2}{-2\sigma_s^2})\\
EXP_{rq}[x] = \exp(\frac{\psi(x)}{-2\sigma_r^2})
$EXP_{rq}$は量子化した色重みのLUTです.
$\phi(x)$と$\psi(x)$は,それぞれ量子化関数,それの逆変換関数になり,例えばルートで量子化する場合は次のようになります.
\phi(x) = \sqrt{x},\\
\psi(x) = x^2,
カラー画像の場合,LUTサイズは$19075=3\times255^2+1$必要ですが,この量子化では$442=\lfloor\sqrt{3\times255^2}\rfloor+1$となり,LUTサイズをかなり小さくできます.
実験結果
実験は,次の環境・実装で行いました.
- CPU: Intel Core-i9 7980XE 18コア,32スレッド,2.60GHz
- OS: Windows 10 64bit
- コンパイラ: Intel Compiler 18
- 並列化: Concurrency
- ベクトル化(SIMD): AVX/AVX2(githubの方には,SSE,AVX512のコードもあります)
まず,非正規化数を抑制した効果の結果です.
パラメータは,$\sigma_r=4$, $\sigma_s=6$, カーネルの大きさは$33\times33$で,画像サイズは$768\times512$です.
非正規化数を抑制するだけで,3倍の高速化に成功しました.
非正規化数の発生状況はパラメータや画像によっても異なるため,場合によってはこれ以上の高速化も達成できます.
なお,PSNRは非正規化数抑制あり・なしともに76.76dBあり,近似していても精度は十分です.
次に,並列化やベクトル化をしない場合から,どの程度速くなったのか順を追ってを見てみます.
パラメータは,$\sigma_r=4$, $\sigma_s=6$, カーネルの大きさは$(33, 33)$で,画像サイズは$768\times512$です.また,計算時間の軸は,対数軸です.
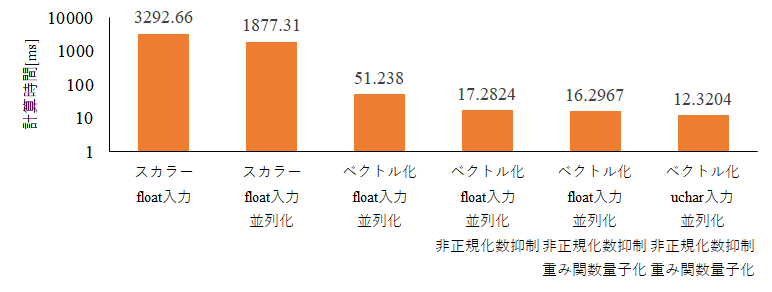
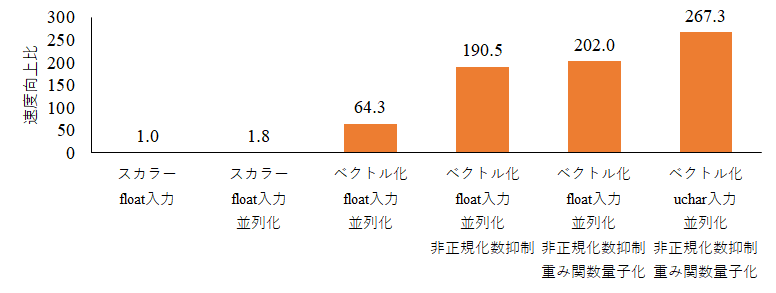
並列化・ベクトル化をするだけで,スカラ実装よりも64倍も速くなっています.
普通は,並列化・ベクトル化までで高速化・最適化が終わってしまいますが,そこから更に非正規化数を抑制することによって190倍まで更に速くできます.
あとは,重み関数を工夫したり,float型ではなくuchar型を入力とすることによって,267倍まで高速化することができました.
ちなみに,実験を行った計算機は18コア32スレッドなのですが,並列化を行った場合の速度向上比が1.8倍と単純に考えて並列化性能が悪すぎます.
検証してみたのですが,どうやら非正規化数の演算は並列化が上手くできないようです.
このあたり詳しい方がおられたら,教えてください.Intelのドキュメントをいろいろ見てみたのですが,分かりません.
最後に,OpenCVのバイラテラルフィルタと比較してみます.「OpenCVの」と書きました,実際はIntel IPPとの比較と思ってもらえばいいです.
パラメータは,$\sigma_r=4$, カーネルの大きさは$(2\times 3\sigma_s+1, 2\times 3\sigma_s+1)$で,$\sigma_s$を変化させています.画像サイズは$768\times512$です.
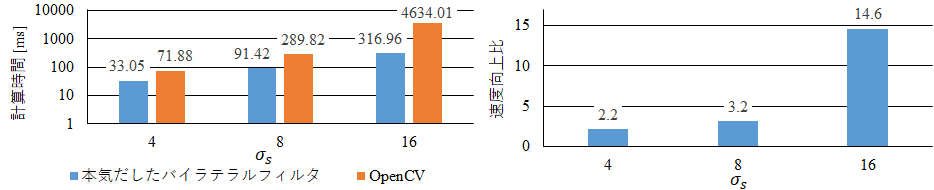
「本気だしたバイラテラルフィルタ」は,IPPよりも2倍~14倍速いです.
PSNRも「本気だしたバイラテラルフィルタ」は80dBを越えていますが,OpenCVは44dBぐらいと低いです.
余談
この投稿に関して,@fukushima1981先生と@dandelion1124さんがtwitterで次のようなやりとりをされていましたw.
いえすw
— Norishige Fukushima (@fukushima1981) 2018年12月5日
おわりに
この記事では,遅いと言われるバイラテラルフィルタをいかに高速化するかについて紹介しました.
今回は紹介しませんでしたが,このアプローチはノンローカルミーンフィルタにも適用でき,githubのほうにはノンローカルミーンフィルタの実装もあります.
明日は,@usk81さんの「OpenCVの本当に動くビルド&インストールガイド」です.


