Python、scipyのcurve_fitを使ってミカエリスメンテン式へのfittingを行う

Pythonのscipyを使ってcurve_fitを利用したミカエリスメンテン式へのfittingを行う。
Pandasを利用してデータを読み込み、seabornを用いてグラフを出力します。
この方法を用いてGoogle Colaboratoryでも描画できます。

モジュールのインポート

まず、必要なモジュールをimportする。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.optimize import curve_fit
import seaborn as sns

データの準備

Pandas形式のデータを作成する。 直接コードに書き込む場合は以下の方法を用いると良い。 1, 2, 3, 4 種類の濃度のデータを3回解析したデータを用いるとする。

#濃度のリスト
x = [1,2,3,4,
     1,2,3,4,
     1,2,3,4,]
#活性のリスト
y = [0.0010,0.0020,0.0025,0.0030,
     0.0015,0.0025,0.0027,0.0032,
     0.0008,0.0017,0.0023,0.0028]
data_1 = pd.DataFrame({'concentration': x, 'activity': y,})

csvファイルの読み込みでもよい。
以下のような中身のcsvファイルに任意の名前をつけてcsvファイルを読み込むと良い。

concentration,activity
1,0.0010
2,0.0020
3,0.0025
4,0.0030
1,0.0015
2,0.0025
3,0.0027
4,0.0032
1,0.0008
2,0.0017
3,0.0023
4,0.0028

以下のコマンドでcsvファイルを読み込む。
google colaboratoryを利用する場合は

#Google colaboratoryにファイルをアップロードする場合
uploaded = files.upload()

#csvファイルの読み込み
data = pd.read_csv("filename.csv")

printを用いてデータリストが正しく作成されていることを確認する。
濃度と活性のデータが1対１で対応していることを確認します。
一つの濃度につき、3種のデータがあります。

print(data_1)
#以下出力
    concentration  activity
0               1    0.0010
1               2    0.0020
2               3    0.0025
3               4    0.0030
4               1    0.0015
5               2    0.0025
6               3    0.0027
7               4    0.0032
8               1    0.0008
9               2    0.0017
10              3    0.0023
11              4    0.0028

試しにこれらのデータを散布図として出力し、傾向を確認する。

sns.scatterplot(data = data_1, x = "concentration", y = "activity")

以下のようなグラフが出力されます。

双曲線にfitting

まず、fittingに用いる関数を用意します。

#ミカエリスメンテン式
#k1がVmax, k2がKmを表しています。
def MM_Eq(x,k1,k2): 
    return  k1*x/(x+k2)

次にcurve fitを用いてfittingを行います。

param, cov = curve_fit(MM_Eq,data_1["concentration"],data_1["activity"])
print(param)
print(cov)

paramにfitting後のk1とk2が格納されます。
k1がVmax, k2がKmに対応します。
covには共分散が出力されます。

次に出力された近似曲線を描画するためのdefを作ります。
この方法により、fittingした結果得られた関数の理想値のリストを作成します。
ここでは100個の点を作成し、曲線の描画に用います。
リスト作成のためのdefをまず用意します。

#近似式に該当した曲線の出力
#曲線を描画するために用いる点の数を指定します。
RES = 100

#maxには濃度の最大値を入力します。
#k1, k2は先ほどの値と同様です。
def graph_plot(max, k1, k2): 
  limit = max + max/10
  x = []
  y = []
  lst = range(0,RES + 1)
  for j in lst:
    i = max/RES * j
    x.append(i)
    y.append(MM_Eq(i,k1,k2))
  return x, y

作成したdefを用いて、実際に点のデータを作成します。
さらにpandas形式に変換し格納します。
data["concentration"].max()は基質濃度の最大値を返します。
param[0],param[1]はそれぞれ出力されたk1とk2を表します。

xs, ys = graph_plot(data_1["concentration"].max(),param[0],param[1])
curve = pd.DataFrame({'concentration': xs, 'activity': ys,})

pandasのリストが正しくできていることを確認します
最大濃度が4、点の数を100 (RES)と指定したため、0.04 ごとにfittingした関数の結果が出力されたリストが得られます。

print(curve)
#以下が出力
     concentration  activity
0             0.00  0.000000
1             0.04  0.000057
2             0.08  0.000113
3             0.12  0.000167
4             0.16  0.000221
..             ...       ...
96            3.84  0.002932
97            3.88  0.002948
98            3.92  0.002964
99            3.96  0.002980
100           4.00  0.002995

試しに散布図を描画します。

sns.scatterplot(data = curve, x = "concentration", y = "activity", )

散布図なので、点が並んでいますが、最終的には折れ線グラフを用いた方がいいと思われます。

グラフの描画

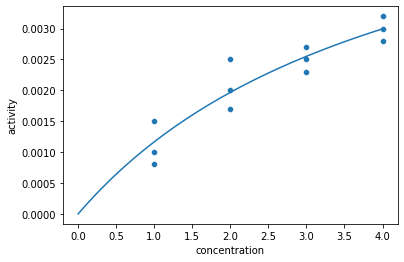
元、データとfittingした関数を重ね合わせた図を出力します。

#入力データの描画
sns.scatterplot(data = data_1, x = "concentration", y = "activity")
#fittingした関数の描画
sns.lineplot(data = curve, x = "concentration", y = "activity")
#pdf形式でファイルを保存する
plt.savefig('filename.pdf')

以下のような画像がダウンロードできます。

平均と標準誤差をプロットしたい場合

#濃度の抽出
data_conc = data_1.concentration.drop_duplicates()

#活性の平均の計算
data_ave = data_1.groupby('concentration').mean()

#活性の平均の標準誤差の計算
data_se = data_1.groupby('concentration').sem()

#図形の描画
plt.errorbar(data_conc.values,data_ave.values, 
             yerr = data_se.values, capsize=5, 
             fmt='o', markersize=10, ecolor='black', 
             markeredgecolor = "black", color='w')
plt.plot(curve['concentration'],curve['activity'], color = 'black')
plt.savefig('filename.pdf')

この場合、以下のような図が出力されます。