はじめに
千葉大学・株式会社Nospareの川久保です.今回は,線形代数における正射影(直交射影)という概念を,その幾何的なイメージがつかめるよう,平易な例を挙げながら説明します.線形回帰,線形判別,主成分分析などの多変量解析の様々な手法において正射影が登場するので,その例も紹介します.
2次元平面における正射影
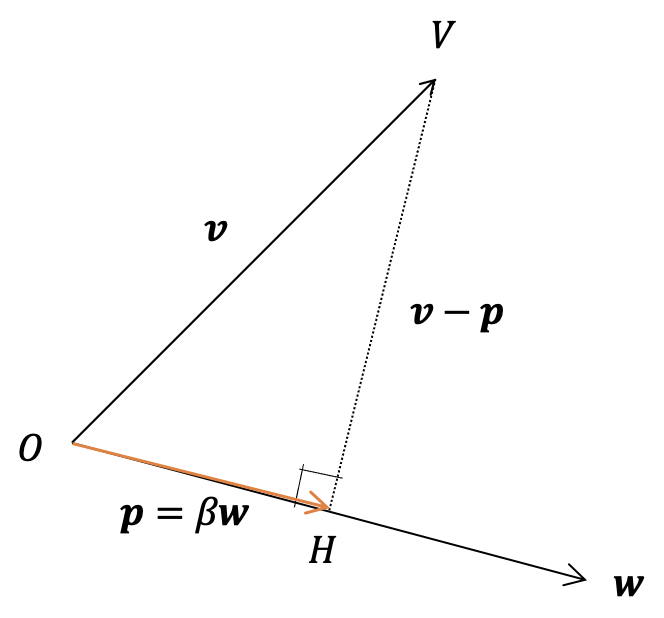
図1のように,2次元ベクトル$\boldsymbol{v}$と$\boldsymbol{w}$が与えられたとします.$\boldsymbol{v}$の端点$V$から$\boldsymbol{w}$に沿う直線に垂線を下ろし,直線と垂線が交わる点を$H$とします.そして,有向線分$\vec{OH}$のベクトルを$\boldsymbol{p}$とすると,$\boldsymbol{p}$のことを,$\boldsymbol{v}$の$\boldsymbol{w}$に対する正射影ベクトルといいます.
スカラー$\beta$を用いて,$\boldsymbol{p} = \beta \boldsymbol{w}$と表せますが,この$\beta$は以下のように求めることができます.$\boldsymbol{w}$と$\boldsymbol{v}-\boldsymbol{p}$は直交するので,内積をとると0になります.すなわち,
$$
\boldsymbol{w}^\top (\boldsymbol{v} - \beta \boldsymbol{w}) = 0
$$
が成り立ちます.これを$\beta$について解くと,
$$
\beta = {\boldsymbol{w}^\top \boldsymbol{v} \over \boldsymbol{w}^\top \boldsymbol{w}}
$$
が求まります.ここで$\boldsymbol{w}^\top \boldsymbol{w} = 1$,すなわち$\boldsymbol{w}$のノルム(長さ)が1のとき,正射影ベクトル$\boldsymbol{p}$の符号付き長さは$\beta = \boldsymbol{w}^\top \boldsymbol{v}$,すなわち$\boldsymbol{w}$と$\boldsymbol{v}$の内積になります.
 図2
図2
数値例を考えます.まず$\boldsymbol{w} = (1,0)^\top$とします.このとき$\boldsymbol{w}^\top \boldsymbol{w} = 1$より,$\boldsymbol{w}$のノルムは1です.ベクトル$\boldsymbol{v} = (2,3)^\top$と$\boldsymbol{w}$の内積は,$\beta = \boldsymbol{w}^\top \boldsymbol{v} = 2$で,$\boldsymbol{v}$の$\boldsymbol{w}$への(つまり$x$軸への)正射影ベクトルは$\beta \boldsymbol{w} = (2,0)^\top$です.
 図3
図3
次に,$\boldsymbol{w} = ({4 \over 5}, {3 \over 5})^\top$とします.このとき$\boldsymbol{w}^\top \boldsymbol{w} = 1$より,$\boldsymbol{w}$のノルムは1です.ベクトル$\boldsymbol{v}_1 = (1, 2)^\top$と$\boldsymbol{w}$の内積は,$\boldsymbol{w}^\top \boldsymbol{v}_1 = 2$より,$\boldsymbol{v}_1$の正射影ベクトルは$2\times({4 \over 5}, {3 \over 5}) = ({8 \over 5}, {6 \over 5})^\top$です.また,$\boldsymbol{v}_2 = (0,{10 \over 3})^\top$の正射影ベクトルも,$\boldsymbol{w}^\top \boldsymbol{v}_2 = 2$より,$({8 \over 5}, {6 \over 5})^\top$です.$({8 \over 5}, {6 \over 5})$に正射影されるのは,どのようなベクトルたちでしょうか.それは$\boldsymbol{w}$との内積が2になるベクトルたちです.すなわち,
$$
{4 \over 5}x + {3 \over 5}y = 2, \tag{1}
$$
を満たす$(x,y)^\top$全体,つまり直線(1)上の点を端点とし,原点からのびる有向線分のベクトル全体です.ところで直線(1)は,法線ベクトルが$\boldsymbol{w} = ({4 \over 5}, {3 \over 5})^\top$ですが,(1)の右辺の値が変わることで,(1)に平行,つまり$\boldsymbol{w} = ({4 \over 5}, {3 \over 5})^\top$に垂直な直線がそれぞれ描かれます.よって,ベクトル$\boldsymbol{w} = ({4 \over 5}, {3 \over 5})^\top$に垂直な直線は,「同じ正射影ベクトルを持つベクトルの端点の集まりである」ということが分かります.
3次元空間における2次元平面への正射影
 図4
図4
次は,3次元空間において,ベクトル$\boldsymbol{v}$を,2つの線形独立なベクトル$\boldsymbol{w}_1$と$\boldsymbol{w}_2$の張る2次元平面へ正射影します.正射影ベクトルを$\boldsymbol{p} = \beta_1 \boldsymbol{w}_1 + \beta_2 \boldsymbol{w}_2$として,スカラー$\beta_1$と$\beta_2$を求めます.ここで,$3 \times 2$の行列$\boldsymbol{W} = [\boldsymbol{w}_1, \boldsymbol{w}_2]$と,$2 \times 1$の列ベクトル$\boldsymbol{\beta} = (\beta_1, \beta_2)^\top$を定義すると,$\boldsymbol{p} = \boldsymbol{W} \boldsymbol{\beta}$と書けます.先ほどと同様にして,$\boldsymbol{v} - \boldsymbol{p} = \boldsymbol{v} - \boldsymbol{W} \boldsymbol{\beta}$と,$\boldsymbol{w}_1, \boldsymbol{w}_2$はそれぞれ直交するので,
\begin{align}
& \boldsymbol{w}_1^\top (\boldsymbol{v} - \boldsymbol{W} \boldsymbol{\beta}) = 0, \\
& \boldsymbol{w}_2^\top (\boldsymbol{v} - \boldsymbol{W} \boldsymbol{\beta}) = 0,
\end{align}
が成り立ちます.これを行列表記すると,
$$
\boldsymbol{W}^\top (\boldsymbol{v} - \boldsymbol{W} \boldsymbol{\beta}) = 0
$$
となります.この方程式を$\boldsymbol{\beta}$について解くと,
$$
\boldsymbol{\beta} = (\boldsymbol{W}^\top \boldsymbol{W})^{-1} \boldsymbol{W}^\top \boldsymbol{v}, \tag{2}
$$
が求まり,正射影ベクトル$\boldsymbol{p}$は,
\begin{align}
\boldsymbol{p} &= \boldsymbol{W} \boldsymbol{\beta} \\
&= \boldsymbol{W} (\boldsymbol{W}^\top \boldsymbol{W})^{-1} \boldsymbol{W}^\top \boldsymbol{v}, \tag{3}
\end{align}
であることが分かります.
一般化
$\boldsymbol{v} \in \mathbb{R}^n$を,$k$個の線形独立な$\boldsymbol{w}_1,\dots,\boldsymbol{w}_k \in \mathbb{R}^n$の張る部分空間に正射影することを考えます.$n \times k$行列$\boldsymbol{W} = [\boldsymbol{w}_1,\dots,\boldsymbol{w}_k]$と$\boldsymbol{\beta} = (\beta_1,\dots,\beta_k)^\top$を定義し,正射影を$\boldsymbol{p} = \boldsymbol{W} \boldsymbol{\beta}$とおきます.先ほどと同様に,$\boldsymbol{v} - \boldsymbol{p} = \boldsymbol{v} - \boldsymbol{W} \boldsymbol{\beta}$と,$\boldsymbol{w}_1,\dots,\boldsymbol{w}_k$はそれぞれ直行することから,
$$
\boldsymbol{W}^\top (\boldsymbol{v} - \boldsymbol{W} \boldsymbol{\beta}) = 0
$$
が成り立ちます.これを$\boldsymbol{\beta}$について解くと,やはり先ほどと同様に,
$$
\boldsymbol{\beta} = (\boldsymbol{W}^\top \boldsymbol{W})^{-1} \boldsymbol{W}^\top \boldsymbol{v},
$$
が求まり,正射影ベクトルは$\boldsymbol{W} (\boldsymbol{W}^\top \boldsymbol{W})^{-1} \boldsymbol{W}^\top \boldsymbol{v}$であることが分かります.
多変量解析の例
線形回帰
線形回帰モデル
$$
\boldsymbol{v} = \boldsymbol{W} \boldsymbol{\beta} + \boldsymbol{\varepsilon}
$$
を考えます.最小二乗推定量$\widehat{\boldsymbol{\beta}} = (\boldsymbol{W}^\top \boldsymbol{W})^{-1} \boldsymbol{W}^\top \boldsymbol{v}$は(2)式そのもので,当てはめ値ベクトル
\begin{align}
\widehat{\boldsymbol{v}} &= \boldsymbol{W} \widehat{\boldsymbol{\beta}} \\
&= \boldsymbol{W} (\boldsymbol{W}^\top \boldsymbol{W})^{-1} \boldsymbol{W}^\top \boldsymbol{v}
\end{align}
は(3)式そのものです.つまり,当てはめ値ベクトル$\widehat{\boldsymbol{v}}$は,目的変数ベクトル$\boldsymbol{v}$を,説明変数たちの張る部分空間($\boldsymbol{W}$の列空間)に正射影したベクトルであるということです.
線形判別
 図5
図5
$k$次元データ$\boldsymbol{v} = (v_1,\dots,v_k)^\top$が,2群のどちらに属すかを判別したいとします.例えば,検査結果の数値から,ある病気であるか,そうでないかを判別したい問題などが挙げられます.この問題に,データのある線形結合$\boldsymbol{w}^\top \boldsymbol{v} = w_1v_1 + \dots + w_kv_k$の値で判別する手法を,線形判別といいます.すでに2群のどちらに属すか分かっている$n$個の$k$次元訓練データから,判別能力が高くなるように$\boldsymbol{w} = (w_1,\dots,w_k)^\top$を推定します.
$\boldsymbol{w}$のノルムを1とします.このとき,データ$\boldsymbol{v}$の線形結合$\boldsymbol{w}^\top \boldsymbol{v}$は,$\boldsymbol{v}$の$\boldsymbol{w}$に対する正射影ベクトルの符号付き長さを表します.つまり,図1における$\beta$の値です.データ点を$\boldsymbol{w}$に正射影したときの目盛の値のイメージです(図5における点線と$\boldsymbol{w}$の延長線の交わる点の目盛りを読むイメージ).この$\beta$の値の大きさによって,データ$\boldsymbol{v}$が,2群のどちらに属すかを決定します.詳細は省略しますが,ある最適な$\boldsymbol{w}$と判別の閾値$\beta$を推定し,以下のような判別関数を構成します.
$$
h(\boldsymbol{v}) = \hat{\boldsymbol{w}}^\top \boldsymbol{v} - \hat{\beta}
$$
そして,$h(\boldsymbol{v}) \geq 0$のとき群1,$h(\boldsymbol{v}) < 0$のとき群2に判別します.方程式$h(\boldsymbol{v}) = 0$は,$\hat{\boldsymbol{w}}$との内積が$\hat{\beta}$となる点の集まりを表す直線で,この直線を境に群1の属す点と群2に属す点の領域に分けられます.
主成分分析
 図6
図6
主成分分析は,$k$次元データ$(v_1,\dots,v_k)^\top$の次元を削減する手法です.簡単化のために,$k=2$次元のデータを1次元に落とすケースを考えます.判別分析のときと同様,ノルム1の$\boldsymbol{w} = (w_1,w_2)^\top$を用いたデータの線形結合$\beta = w_1v_1 + w_2v_2$を考えます.判別分析でも説明しましたが,この$\beta$という値は,データ点$\boldsymbol{v}$を$\boldsymbol{w}$という軸に正射影したときの目盛の値のイメージ(図6における点線と$\boldsymbol{w}$の延長線の交わる点の目盛を読むイメージ)で,2次元データ$\boldsymbol{v}$を1次元の$\beta$に次元削減しています.詳細は省略しますが,$\boldsymbol{w}$の値は,次元削減後のデータの分散が大きくなるように決定します.
よく出てくる簡単な例は,英語の点数$v_1$と数学$v_2$の2次元データです.2次元データ$\boldsymbol{v} = (v_1,v_2)^\top$を1次元データに次元削減する単純な方法は,合計点$v_1+v_2$を計算し,この合計点で順位付けを行う方法で,これは$\boldsymbol{w} = ({1 \over \sqrt{2}},{1 \over \sqrt{2}})^\top$に対応します.主成分分析では,次元削減後のデータの分散が大きくなるような線形結合のウェイト$\boldsymbol{w} = (w_1,w_2)^\top$を求めるため,必ずしも英語と数学のウェイトを等しくすることが最適とは限りません.
おわりに
株式会社Nospareには,統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospare までお問い合わせください.