はじめに
千葉大学・株式会社Nospareの川久保です.今回はジニ係数と呼ばれる所得などの不平等度を測る指標と,不平等度を視覚的に図示したローレンツ曲線について紹介します.学術的には,経済統計と呼ばれる分野の概念ですが,久保川・国友「統計学」や,倉田・星野「入門統計解析」などの,統計学の代表的な入門書でも解説されています.
有限母集団におけるローレンツ曲線とジニ係数
まずは,所得データなどの母集団が$x_1,x_2,\dots,x_N$と有限個の要素から構成されている状況における,ローレンツ曲線とジニ係数について説明します.もちろん実社会における母集団は,実際には有限です(日本の人口は約1億2600万人,世帯総数は約4800万世帯など).母集団の所得分布に確率分布(対数正規分布など)を当てはめて所得データを解析することも多いですが,そのケースについては次節で説明します.
ローレンツ曲線
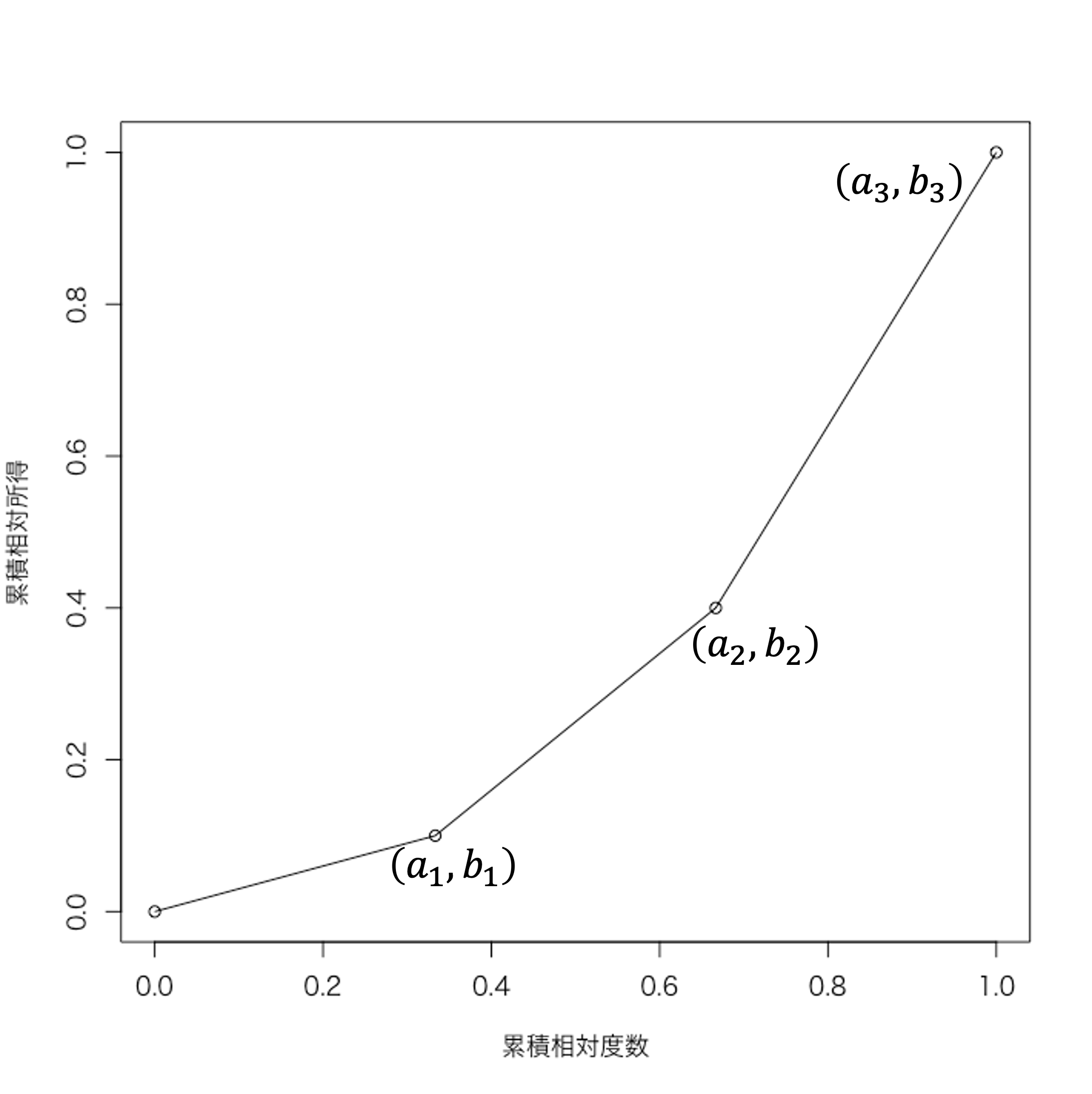
ローレンツ曲線とは,所得を低い順に並び替えて,累積相対度数を$x座標$,累積相対所得を$y座標$としてプロットした点を結んでいった曲線のことです.$x_{1},x_{2},\dots,x_{N}$を,低い順に並べた所得データとします.$i$番目に低い所得$x_{i}$をもつ世帯の累積相対度数$a_i$と累積相対所得$b_i$はそれぞれ,
$$
\tag{1}
a_i = \frac{i}{N}, \quad b_i = \frac{x_{1}+x_{2}+\dots+x_{i}}{x_{1}+x_{2}+\dots+x_{N}} = \frac{x_1+x_2+\dots+x_i}{N\bar{x}}
$$
です.ただし,$\bar{x} = N^{-1}(x_1+x_2+\dots+x_N)$は,母集団の平均所得です.例として$x_1 = 100, x_2 = 300, x_3 = 600$という所得を持つ3つの世帯だけから成る社会を考えます.このとき,
$$
(a_1,b_1) = (\frac{1}{3}, \frac{1}{10}), \quad (a_2,b_2) = (\frac{2}{3}, \frac{4}{10}), \quad (a_3, b_3) = (1,1)
$$
ですので,ローレンツ曲線は下図のようになります.この社会においては,全体の33パーセントの世帯で10パーセントの所得を,66パーセントの世帯で40パーセントの所得を得ていることを意味します.ローレンツ曲線は定義上,必ず45度線の下を通りますが,45度線から離れているほどその社会は不平等であることを意味します.その社会における全世帯が同じ所得を得ている場合,ローレンツ曲線は45度線上と一致します.
ジニ係数
ジニ係数は,ローレンツ曲線と45度線で囲まれる面積の2倍として定義されます.ジニ係数は0から1の間の値をとり,値が大きいほどその社会は不平等であると解釈されます.ローレンツ曲線が45度線と一致する完全平等の状態でジニ係数は0,1つの世帯だけが所得を得ている状態のときジニ係数は1になります.

まずは,4つの世帯だけから成る社会におけるジニ係数$G$を計算してみます.上図の三角形2つと台形1つの面積の和の2倍がジニ係数なので,
\begin{align}
G &= (a_1-b_1)a_1 + (a_1-b_1 + a_2-b_2)(a_2-a_1) + (a_2 - b_2 + a_3 - b_3)(a_3-a_2) + (a_3 - b_3)(1-a_3) \\
&= (a_1-b_1)a_2 + (a_2-b_2)(a_3-a_1) + (a_3-b_3)(1-a_2)
\end{align}
と計算されます.これを一般化すると,
$$
G = \sum_{i=1}^{N-1}(a_i - b_i)(a_{i+1} - a_{i-1})
$$
と書けます.ここで,$a_0 = 0$とします.(1)式の$a_i,b_i$を代入すると,
\begin{align}
G &= \frac{2}{N} \sum_{i=1}^{N-1} \left( \frac{i}{N} - \frac{x_1+x_2+\dots+x_i}{N\bar{x}} \right) \\
&= \frac{2}{N} \sum_{i=1}^\color{red}{N} \left( \frac{i}{N} - \frac{x_1+x_2+\dots+x_i}{N\bar{x}} \right) \\
&= \frac{N+1}{N} - \frac{2}{N^2\bar{x}}\sum_{i=1}^N \sum_{j=1}^i x_j \tag{2}
\end{align}
と求まります.
平均絶対差分としてのジニ係数
ジニ係数$G$は,以下のような表現も可能です.
$$
\tag{3}
G = \frac{1}{2N^2\bar{x}} \sum_{i=1}^N \sum_{j=1}^N |x_i - x_j|
$$
(3)式の$N^{-2}\sum_{i=1}^N \sum_{j=1}^N |x_i - x_j|$の部分は,その社会における全ての世帯の組み合わせにおける所得の差の平均を計算しています.これを$\bar{x}$で割ることによって,スケールを相殺し相対化しています.世帯間の所得の差の大きさから,不平等度を計算しているわけです.
(3)式を変形すると(2)式と一致することは,以下のように示すことができます.(3)式において,以下の変形が成り立ちます.
\begin{align}
\sum_{i=1}^N \sum_{j=1}^N |x_i - x_j| &= 2\sum_{i=1}^N \sum_{j=1}^i (x_i - x_j) \\
&= 2\sum_{i=1}^N ix_i - 2\sum_{i=1}^N \sum_{j=1}^i x_j \\
&= 2\sum_{i=1}^N ix_i - 2\sum_{j=1}^N \sum_{i=j}^N x_j \\
&= 2\sum_{i=1}^N ix_i - 2\sum_{j=1}^N (N-j+1)x_j \\
&= 2\sum_{i=1}^N ix_i + 2\sum_{j=1}^Njx_j - 2(N+1)\sum_{j=1}^Nx_j \\
&= 4\sum_{i=1}^N ix_i - 2(N+1)N\bar{x}
\end{align}
よって(3)式のジニ係数は,以下のように変形できます.
$$
G = \frac{2}{N^2\bar{x}}\sum_{i=1}^N ix_i - \frac{N+1}{N} \tag{3'}
$$
一方で(2)式は,
\begin{align}
G &= \frac{N+1}{N} - \frac{2}{N^2\bar{x}}\sum_{i=1}^N\sum_{j=1}^ix_j \\
&= \frac{N+1}{N} - \frac{2}{N^2\bar{x}}\sum_{j=1}^N \sum_{i=j}^N x_j \\
&= \frac{N+1}{N} - \frac{2}{N^2\bar{x}}\sum_{j=1}^N (N-j+1)x_j \\
&= \frac{N+1}{N} - \frac{2}{N^2\bar{x}} \left\{ (N+1)\sum_{j=1}^N x_j - \sum_{j=1}^N jx_j \right\} \\
&= \frac{N+1}{N} - \frac{2}{N^2\bar{x}} \left\{ (N+1)N\bar{x} - \sum_{i=1}^N ix_i \right\} \\
&= \frac{2}{N^2\bar{x}}\sum_{i=1}^N ix_i - \frac{N+1}{N}
\end{align}
と変形でき,(3')式と同じであることを確認できます.
母集団に確率分布を仮定したケース
次に,母集団の所得分布として,密度関数$f(x) \ (x>0)$を持つ確率分布を仮定するケースを考えます.この確率分布の累積分布関数を$F(x) = \int_0^x f(t)dt$,その逆関数(分位点関数)を$F^{-1}(p) \ (0\leq p\leq 1)$とします.
ローレンツ曲線
確率分布$f$の$100p$パーセント点(下位$100p$パーセント)の所得を持つ世帯までの累積相対所得を$L(p)$という関数で表わしたとき,$(p,L(p))$の成す軌跡がローレンツ曲線です.$z$を$f$の$100p$パーセント点,すなわち,$p = F(z) = \int_0^z f(x)dx$が成り立つ点であるとします.このとき,
$$
L(p) = \frac{\int_0^z xf(x)dx}{\int_0^\infty xf(x)dx} = \frac{1}{\mu}\int_0^z xf(x)dx
$$
となります.ただし,分母の$\mu$は確率分布$f$の平均で,分子は部分積率(partial moment)です.ここで,$x = F^{-1}(u)$なる変数変換を考えると,$f(x)dx = du, F^{-1}(p) = z, F^{-1}(0) = 0$より,
$$
\tag{4}
L(p) = \frac{1}{\mu} \int_0^p F^{-1}(u)du
$$
と書けます.
ジニ係数
ジニ係数は,45度線とローレンツ曲線で囲まれる領域の面積の2倍なので,
\begin{align}
G &= 2\int_0^1(p - L(p))dp \\
&= 1 - 2\int_0^1 L(p)dp
\end{align}
です.ここで(4)式より,$L(p)$の導関数は$L'(p) = \mu^{-1}F^{-1}(p)$であることに気をつけると,部分積分を用いて,
\begin{align}
G &= 1 - 2\left[ p L(p) \right]_0^1 + 2\int_0^1 pL'(p)dp \\
&= 1 - 2\{ 1\cdot L(1) - 0\cdot L(0) \} + \frac{2}{\mu}\int_0^1 pF^{-1}(p)dp \\
&= \frac{2}{\mu}\int_0^1 pF^{-1}(p)dp - 1
\end{align}
と式変形できます.ここでもう1度,$x = F^{-1}(p)$なる変数変換を行うと,
\begin{align}
\tag{5}
G &= \frac{2}{\mu}\int_0^\infty F(x) xf(x)dx - 1 \\
&= \frac{2}{\mu} \left\{ \int_0^\infty xF(x)f(x)dx - \frac{\mu}{2} \right\}
\end{align}
とさらに変形できます.$X \sim f(x)$とすると,
\begin{align}
E[F(X)] &= \int_0^\infty F(x)f(x)dx \\
&= \int_0^1 pdp \quad (p = F(x), \ f(x)dx = dp) \\
&= \frac{1}{2}
\end{align}
が成り立つので,
\begin{align}
G &= \frac{2}{\mu} \big\{ E[XF(X)] - E[X] E[F(X)] \big\} \\
&= \frac{2}{\mu} Cov(X, F(X))
\end{align}
が得られます.
別の表現として,
$$
\tag{6}
G = 1 - \frac{1}{\mu} \int_0^\infty \{ 1 - F(x) \}^2 dx
$$
も得られるのですが,それは以下のようにして示されます.$\{ 1 - F(x) \}^2$を$x$で微分すると,$-2f(x)\{ 1 - F(x) \}$となるので,(6)式に部分積分を用いると,
\begin{align}
G &= 1 - \frac{1}{\mu} \left[ x \{ 1 - F(x) \}^2 \right]_0^\infty - \frac{2}{\mu} \int_0^\infty xf(x)\{1 - F(x) \} dx \\
&= 1 - \frac{2}{\mu}\int_0^\infty xf(x)dx + \frac{2}{\mu} \int_0^\infty xF(x)f(x)dx \\
&= \frac{2}{\mu} \int_0^\infty xF(x)f(x)dx - 1
\end{align}
となり,(5)式と一致することが確認できます.
さらに別の表現として,
$$
G = \frac{1}{\mu} \int_0^\infty F(x)\{ 1-F(x) \}dx
$$
も得られますが,部分積分を用いて(6)式の変形と同様に示せます.
平均絶対差分としてのジニ係数
母集団に確率分布を仮定した際も,ジニ係数は以下のような平均絶対差分を用いた定義も可能です.
\begin{align}
G &= \frac{1}{2\mu} E[|X - Y|] \\
&= \frac{1}{2\mu}\int_0^\infty \int_0^\infty |x - y| \ f(x)f(y)dxdy
\end{align}
ただし,$X$と$Y$は互いに独立に$f$にしたがう確率変数です.これが(6)式と一致することは,以下のように確認することができます.まず,
\begin{align}
E[|X - Y|] &= E[X] + E[Y] - 2E[\min(X,Y)] \\
&= 2\mu - 2E[\min(X,Y)]
\end{align}
が成り立ちます.ここで確率変数$\min(X,Y)$の密度関数は,$2f(x)\{ 1 - F(x) \}$ですが,これは$-\{ 1 - F(x) \}^2$を$x$で微分したものです.よって,部分積分を用いると,
\begin{align}
G &= \frac{1}{2\mu} \big( 2\mu - 2E[\min(X,Y)] \big) \\
&= 1 - \frac{1}{\mu}\int_0^\infty x\cdot 2f(x)\{1 - F(x) \}dx \\
&= 1 + \frac{1}{\mu}\left[ x \{ 1 - F(x) \}^2 \right]_0^\infty - \frac{1}{\mu} \int_0^\infty \{ 1 - F(x) \}^2 dx \\
&= 1 - \frac{1}{\mu} \int_0^\infty \{ 1 - F(x) \}^2 dx
\end{align}
となり,(6)式と一致します.
確率分布を仮定することのメリット
母集団の所得分布に,パラメトリックな確率分布を仮定することのメリットとしては,ジニ係数やローレンツ曲線が,確率分布のパラメータの関数で表現できるということが挙げられます.つまり,低次元のパラメータを推定することで,ジニ係数やローレンツ曲線が推定できるため,分布の仮定が正しければ推定は効率的になります.例えば,母集団の所得分布として対数正規分布$LN(\mu,\sigma^2)$を仮定した場合,ローレンツ曲線は$L(p) = \Phi(\Phi^{-1}(p) - \sigma)$,ジニ係数は$2\Phi(\sigma/\sqrt{2}) - 1$となり,ともにパラメータ$\sigma$のみの関数となります.ただし$\Phi(\cdot)$は標準正規分布関数の累積分布関数です.他の様々な確率分布に対して,ローレンツ曲線とジニ係数のパラメータの関数としての表現が得られています.
おわりに
株式会社Nospareには,統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospare までお問い合わせください.
