はじめに
千葉大学・株式会社Nospareの川久保です.今回は,二値分類モデルのパフォーマンス評価に用いられる,ROC曲線とAUCと呼ばれる指標を説明します.
感度と特異度
ROC(receiver operating characteristic)曲線とは,ロジスティック回帰モデルなどの二値分類モデルの異なる閾値ごとのパフォーマンスを,二次元平面に図示したものです.より具体的には,横軸に偽陽性率(false positive rate, FPR),縦軸に真陽性率(true positive rage, TPR)をとり,モデルで推定された陽性の確率($y=1$が実現する確率)がいくつ以上であれば陽性と予測するかの閾値を変化させ,偽陽性率と真陽性率の組のプロットを結んだ曲線です.
| 陰性と分類($B$) | 陽性と分類($B^c$) | |
|---|---|---|
| 陰性が真($A$) | 真陰性(true negative, TN) | 偽陽性(false positive, FP) |
| 陽性が真($A^c$) | 偽陰性(false negative, FN) | 真陽性(true positive, TP) |
偽陽性率と偽陰性率を説明するために,上のような混同行列を用意します.混同行列の左上のセルは「実際は陰性であり,かつ陰性と分類するとき」であり,これを真陰性(true negative, TN)と呼びます.以下同様にして,偽陽性(false positive, FP),偽陰性(false negative, FN),真陽性(true positive, TP)を定義します.このとき偽陽性率(FPR)は「陰性が真あるという条件のもと,陽性と誤って分類してしまう確率」,すなわち
\tag{1}
\mathrm{FPR} = \frac{\mathrm{FP}}{\mathrm{TN} + \mathrm{FP}}
と定義されます.上の数式における$\mathrm{FP}$および$\mathrm{TN}$は,それぞれその「確率」ですが,観測データにおける「人数(件数)」だとみなしても問題ありません(その場合,計算される割合は推定値と理解されます).後に,条件付き確率の概念を用いて説明しなおします.真陽性率(TPR)は「陽性が真であるという条件のもと,陽性と正しく分類できる確率」,すなわち
\tag{2}
\mathrm{TPR} = \frac{\mathrm{TP}}{\mathrm{TP} + \mathrm{FN}}
と定義されます.
なお,特に医学や疫学分野における臨床検査の精度の指標として,$\mathrm{TPR}$は感度(sensitivity),$1 - \mathrm{FPR}$は特異度(specificity)とも呼ばれます.新型コロナウイルス感染症の流行時に,PCR検査の精度を議論するという文脈で,感度や特異度という用語は専門外の方の耳にも触れる機会が多かったのではないでしょうか(私も医学や疫学は専門外だったので,そのとき初めてこの用語を知りました).感度も特異度も,この値は高ければ高いほど望ましいのですが,この両者はトレードオフの関係にあります.つまり,感度が高くなるように閾値を設定すれば,特異度は低くなってしまい,逆は逆です.そのトレードオフの関係を図示したのがROC曲線なのですが,これは後ほど説明します.
条件付き確率にもとづいた説明
正しい状態が陰性であるという事象を$A$であるとし,陰性と分類する事象を$B$とします.このとき,正しい状態が陽性であるという事象は,正しい状態が陰性であるという事象の余事象なので$A^c$です.同様に陽性と分類する事象は$B^c$です.この事象を用いると,真陰性の確率は$\mathrm{TN} = P(A \cap B)$とあらわせ,以下同様に$\mathrm{FP} = P(A \cap B^c), \ \mathrm{FN} = P(A^c \cap B), \ \mathrm{TP} = P(A^c \cap B^c)$とあらわされます.
さて,偽陽性率(FPR)は「陰性が真であるという条件のもと,陽性と誤って分類してしまう確率」と定義されますが,これは「陰性($A$)を所与とした,陽性と分類($B^c$)する条件付き確率」のことです.すなわち,$\mathrm{FPR} = P(B^c \mid A)$ですが,条件付き確率の定義から,
\begin{align}
\mathrm{FPR} &= P(B^c \mid A) \\
&= \frac{P(A \cap B^c)}{P(A)} \\
&= \frac{P(A \cap B^c)}{P(A \cap B) + P(A \cap B^c)} \\
&= \frac{\mathrm{FP}}{\mathrm{FP} + \mathrm{TN}}
\end{align}
となり,(1)式の定義と一致します.同様に,真陽性率(TPR)は「陽性($A^c$)を所与とした,陽性と分類($B^c$)する条件付き確率」なので,
\begin{align}
\mathrm{TPR} &= P(B^c \mid A^c) \\
&= \frac{P(A^c \cap B^c)}{P(A^c)} \\
&= \frac{P(A^c \cap B^c)}{P(A^c \cap B) + P(A^c \cap B^c)} \\
&= \frac{\mathrm{TP}}{\mathrm{FN} + \mathrm{TP}}
\end{align}
となり,(2)式の定義と一致します.このように偽陽性率および真陽性率は,真の状態を所与とした条件付き確率として定義されます.名称どおり受け取ると「偽陽性の確率」「真陽性の確率」となってしまいますが,何で条件づけているのか(分母は何なのか)を意識することが大切です.
陽性的中率と陰性的中率
やや脱線しますが,条件付き確率に関してもう1つの概念を紹介します.同じ「陽性の確率」でも,所与とする条件が真の状態ではなく,検査の結果である場合,これまでと全く異なった概念になります.陽性的中率(positive predictive value, PPV)は「陽性と分類($B^c$)されるという条件のもとで,実際に陽性である($A^c$)条件付き確率」のことで,
\begin{align}
\mathrm{PPV} &= P(A^c \mid B^c) \\
&= \frac{P(A^c \cap B^c)}{P(B^c)} \\
&= \frac{P(A^c \cap B^c)}{P(A \cap B^c) + P(A^c \cap B^c)} \\
&= \frac{\mathrm{TP}}{\mathrm{TP} + \mathrm{FP}}
\end{align}
とあらわされます.同様に,陰性的中率(negative predictive value, NPV)は「陰性と分類($B$)されるという条件のもとで,実際に陰性である($A$)条件付き確率」のことで,
\begin{align}
\mathrm{NPV} &= P(A \mid B) \\
&= \frac{P(A \cap B)}{P(B)} \\
&= \frac{P(A \cap B)}{P(A \cap B) + P(A^c \cap B)} \\
&= \frac{\mathrm{TN}}{\mathrm{TN} + \mathrm{FN}}
\end{align}
とあらわされます.実際の因果関係は,陽性や陰性という真の状態を原因として,検査の結果が陽性と判定されやすかったり陰性と判定されやすかったりするわけです.一方で陽性的中率と陰性的中率は,その結果を条件づけた原因の条件付き確率を求めていることになり,ベイズの定理の文脈でも説明されます.
感度と特異度のトレードオフ
感度($= \mathrm{TPR}$)と特異度($=1 - \mathrm{FPR}$)に話を戻します.$\mathrm{TPR} = \mathrm{TP} / (\mathrm{FN} + \mathrm{TP})$という定義に気をつけると,感度を上げるには,閾値を下げて陽性に分類する確率を上げればよいです.しかしこのとき一方で,$1 - \mathrm{FPR} = \mathrm{TN} / (\mathrm{TN} + \mathrm{FP})$であるため,陽性に分類する確率を上げると特異度は下がってしまいます.つまり,感度と特異度はトレードオフの関係にあるわけです.
ROC曲線とAUC
ROC曲線とは,このトレードオフ関係を二次元平面に図示したものです.異なる閾値ごとにFPRとTPRをデータから計算(推定)し,その組のプロットを曲線で結んだものです.閾値が1からスタートしますが,このとき陽性と分類する確率($P(B^c) = \mathrm{FP} + \mathrm{TP}$)は0なので,FPRもTPRも0です.よってまず,原点$(0,0)$に点がプロットされます.閾値を徐々に小さくしていくと,FPRもTPRも大きくなっていきますが,FPRは特異度から1を引いた値なので,小さければ小さいほど望ましく,TPRは感度と等しいため大きければ大きいほど望ましいです.つまり閾値を小さくしていったときに,FPRの増加は極力抑えられ,一方でTPRの増加は急激であるほど望ましいわけです.よってROC曲線は基本的に45度線より上側を通ります.なお,閾値を小さくしていき0としたとき,陽性と分類する確率は1なので,FPRもTPRも1になり,最後は座標$(1,1)$に点がプロットされます.
AUC(area under curve)とは,ROC曲線と横軸の間の面積で,これが大きければ大きいほど(1に近ければ近いほど)望ましいという指標です.
ROC曲線を描いてみる
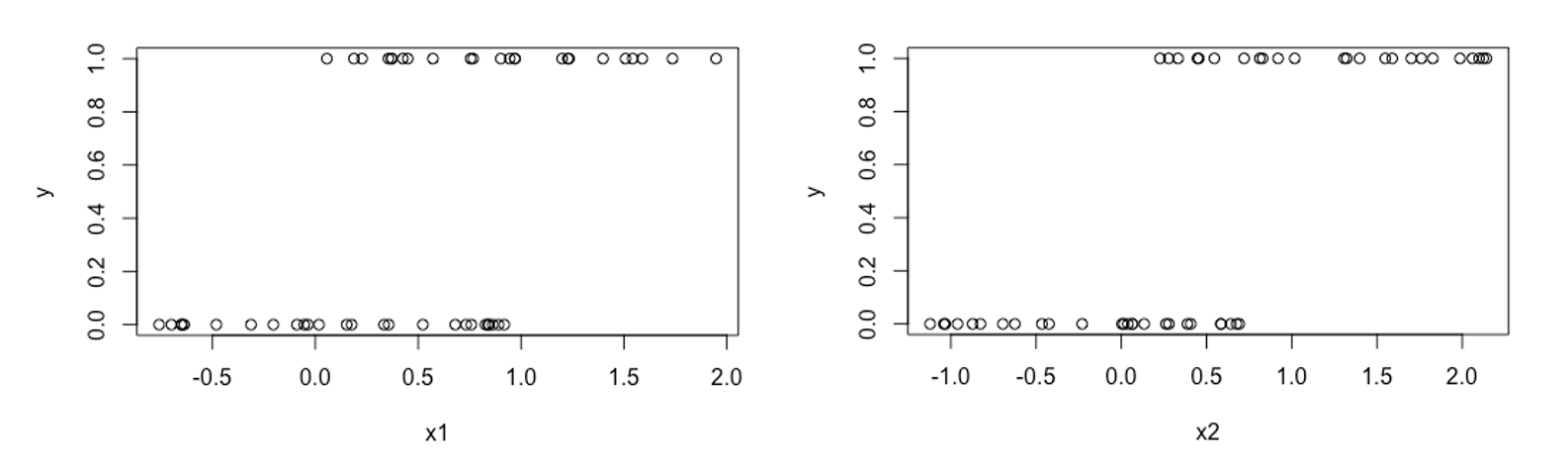
二値の目的変数$y$を説明変数が$x_1, x_2$と2種類あり,$(x_1,y)$と$(x_2,y)$のプロットが,それぞれ上図のようになっているとします.このとき,それぞれロジスティック回帰モデルをあてはめ,推定された当てはめ値($y=1$となる確率)をもとにROC曲線を描いてみます.直感的には,$x_1$よりも$x_2$の方が$y$をよく分類できそうなので,$x_2$を用いたモデルの方がROC曲線は45度線から上に離れていきそうです.ROC曲線の描き方を理解するために,Rの自作関数で作成してみます.
> myroc <- function(df){
# 入力dfは,1列目がy(0or1),2列目がロジスティック回帰で推定された当てはめ値
# 当てはめ値で降順にソート
df <- df[order(df[,2], decreasing = TRUE),]
# ROC曲線のプロットを格納する行列
rocplot <- matrix(nrow = nrow(df)+2, ncol = 2)
rocplot[1,] <- 0 # 原点(0,0)
rocplot[nrow(rocplot),] <- 1 # 座標(1,1)の点
num1 <- sum(df[,1]) # y=1の観測数 (TPRの分母)
num0 <- nrow(df) - num1 # y=0の観測数 (FPRの分母)
FP <- 0 # FPの観測数 (閾値1のときの初期値)
TP <- 0 # TPの観測数 (閾値1のときの初期値)
for(i in 1:nrow(df)){
if(df[i,1] == 1){
# 閾値 = df[i,2]としたとき,i行目までの観測はすべてpositiveに分類される
# よって真がpositive (y=1)である場合,TPは1増える
TP <- TP + 1
}else{
# 真がnegative (y=0)である場合,FPは1増える
FP <- FP + 1
}
# ROC曲線のx座標 (FPR)
rocplot[i+1,1] <- FP / num0
# ROC曲線のy座標 (TPR)
rocplot[i+1,2] <- TP / num1
}
# 原点(0,0)から(1,1)までの点を,線で結ぶ
plot(rocplot, type = "l")
}
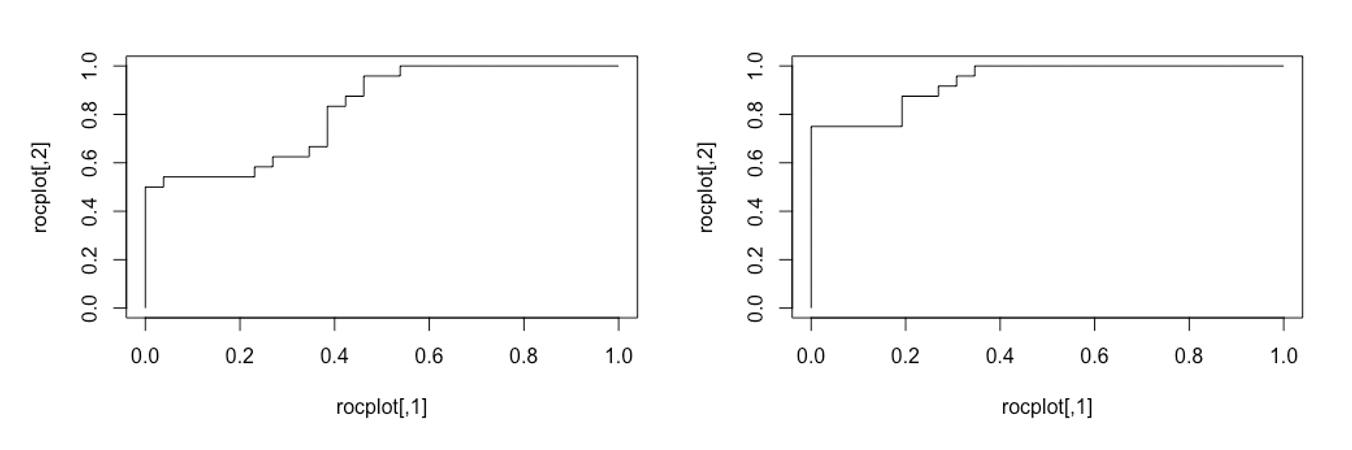
myroc関数の引数は,1列目が目的変数$y \ (=0,1)$,2列目がロジスティック回帰モデルで推定された当てはめ値です.まず,2列目の当てはめ値について降順でソートします.ROC曲線を描く際に1から0に向かって変化させていく閾値は,実際には連続的に変化させるのではなく,推定された当てはめ値で不連続に変化させます.よって推定されるROC曲線は,原点(0,0)と(1,1)の間の,サンプルサイズ分の点を結んだ線になります.さらに,閾値を変化させる度に,FPRもしくはTPRのどちらかしか上昇しないので,階段状に折れ線が描かれます.描かれたROC曲線は,それぞれ下図の左($x_1$)と右($x_2$)です.予想どおり,右の図の方が,45度線から大きく上に乖離していることがわかります.ROC曲線の描画とAUCを計算するRのライブラリとしてpROCというものがあります.これで計算したAUCはそれぞれ,0.8205と0.9375でした.
上の自作関数にあるとおり,ROC曲線を描く際には,当てはめ値の「順番」の情報のみが必要で,その絶対的な大きさは必要ありません.つまり,推定された$y=1$を実現する確率の精確性を測る指標ではないことに気をつけてください.
仮説検定の2種類の誤り
統計的仮説検定における2種類の誤りのトレードオフ関係も,感度と特異度のトレードオフの関係と同様に説明されます.
| $H_0$を棄却しない | $H_0$を棄却する | |
|---|---|---|
| $H_0$が真 | 正しい | 第1種の誤り |
| $H_1$が真 | 第2種の誤り | 正しい |
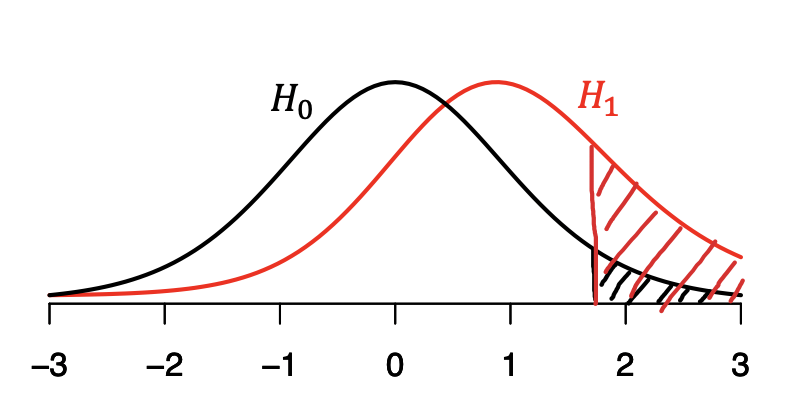
上の表のように,仮説検定の意思決定には2種類の誤りがあります.第1種の誤りは「帰無仮説$H_0$が正しいときに,$H_0$を棄却してしまう」誤りのことです.この確率が$\alpha$以下の検定を,有意水準$\alpha$の検定と呼び,当然$\alpha$の値は小さい方が望ましいです.一方で,第2種の誤りは「対立仮説$H_1$が正しいときに,$H_0$を棄却しない」誤りのことです.$H_0$を棄却する確率を検出力と呼びますが,$H_1$のもとでの検出力が高い,すなわち第2種の誤りの確率は小さい方が望ましいです.
しかしながら,$\alpha$を小さくしようとすると,検出力も小さくなってしまいます.上の図は,$H_0$のもとでの検定統計量の分布(密度関数)と,$H_1$のもとでの検定統計量の分布をあらわしています.上側のみに棄却域を設定する片側検定の場合,黒の斜線部の面積が,第1種の誤りが生じる確率$\alpha$をあらわしていて,赤の斜線部の面積が,$H_1$のもとでの検出力をあらわしています.棄却域を定める臨界値が大きくなればなるほど(棄却域が右にシフトすればするほど),黒の面積も赤の面積も小さくなります.すなわち,第1種の誤りと第2種の誤りのトレードオフ関係を示しています.
おわりに
株式会社Nospareには,統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospare までお問い合わせください.