はじめに
千葉大学・株式会社Nospareの川久保です.今回は初学者向けの内容になりますが,線形回帰モデルの小ネタ集です.私が学部生に講義を行ったりゼミを受け持ったりしているなかで,学生がつまずきやすかったり,気付きにくかったりしているなと感じるポイントを,いくつかピックアップして解説します.
データを対数変換したときの回帰係数の解釈
しばしば,被説明変数$y$または説明変数$x$を対数変換した上で,線形回帰モデルを当てはめます.このときの回帰係数の値の解釈について説明します.
準備1
変換なしの以下の線形回帰モデルを考えます.
$$
y_i = \beta_0 + \beta_1x_{1i} + \dots + \beta_k x_{ki} + \varepsilon_i, \quad \varepsilon_i \overset{\mathrm{iid}}{\sim} (0,\sigma^2), \quad i = 1,\dots,n
$$
このモデルにおける$\beta_1$の解釈は「他の変数を一定として$x_1$のみを1増加させたとき,$y$は平均的に$\beta_1$だけ増加する」となります.
準備2
$\log(1+x)$を$x = 0$まわりで1次近似すると,$\log(1+x) \approx x$となります.この関係性から,
\begin{align}
\log y' - \log y &= \log {y' \over y} \\
&= \log \left( 1 + {y' - y \over y} \right) \\
&\approx {y' - y \over y}
\end{align}
が導かれます.つまり$y$から$y'$への変化率は,$\log y' - \log y$で近似されるということです.
被説明変数の対数変換
被説明変数$y$を対数変換した,以下のような線形回帰モデルを考えます.
$$
\log y_i = \beta_0 + \beta_1 x_{1i} + \dots + \beta_k x_{ki} + \varepsilon_i, \quad \varepsilon_i \overset{\mathrm{iid}}{\sim} (0,\sigma^2), \quad i = 1,\dots,n
$$
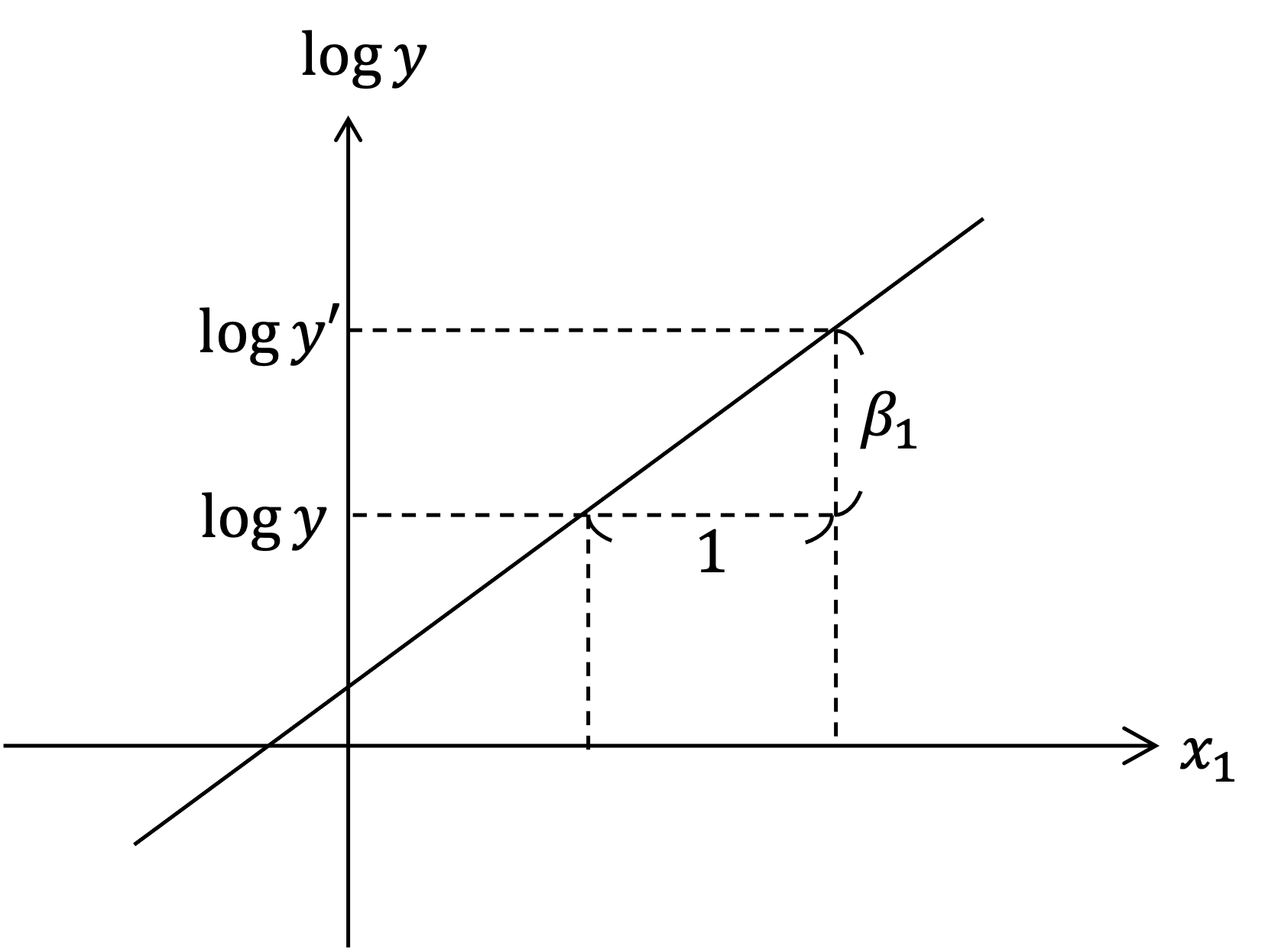
このモデルにおける$\beta_1$の解釈を考えます.準備1での説明を直接適用すると「他の変数を一定として$x_1$のみを1増加させたとき,$\log y$は平均的に$\beta_1$だけ増加する」となります.この解釈自体は正しいのですが,元の$y$のスケールで解釈したい場合不都合です.そこで「$\log y$が$\beta_1$だけ増加するとき,元の$y$はどれだけ変化するのか」を考えます.$y$が$y'$に変化したとします(上図参照).このとき,準備2で説明した近似式から,
\begin{align}
\beta_1 &= \log y' - \log y \\
&\approx {y' - y \over y}
\end{align}
となることが分かります.つまり$\beta_1$を$y$のスケールで解釈すると「他の変数を一定として$x_1$のみを1増加させたとき,$y$は平均的に約100$\beta_1$パーセントだけ増加する」となります.変化率をパーセントの単位で表すため,100倍しています.例えば$\beta_1$が0.07と推定された場合,$100 \times 0.07 = 7$パーセントの増加となります.
説明変数の対数変換
次に説明変数$x_1$を対数変換した以下のモデルを考えます.
$$
y_i = \beta_0 + \beta_1 \log x_{1i} + \dots + \beta_k x_{ki} + \varepsilon_i, \quad \varepsilon_i \overset{\mathrm{iid}}{\sim} (0,\sigma^2), \quad i = 1,\dots,n
$$
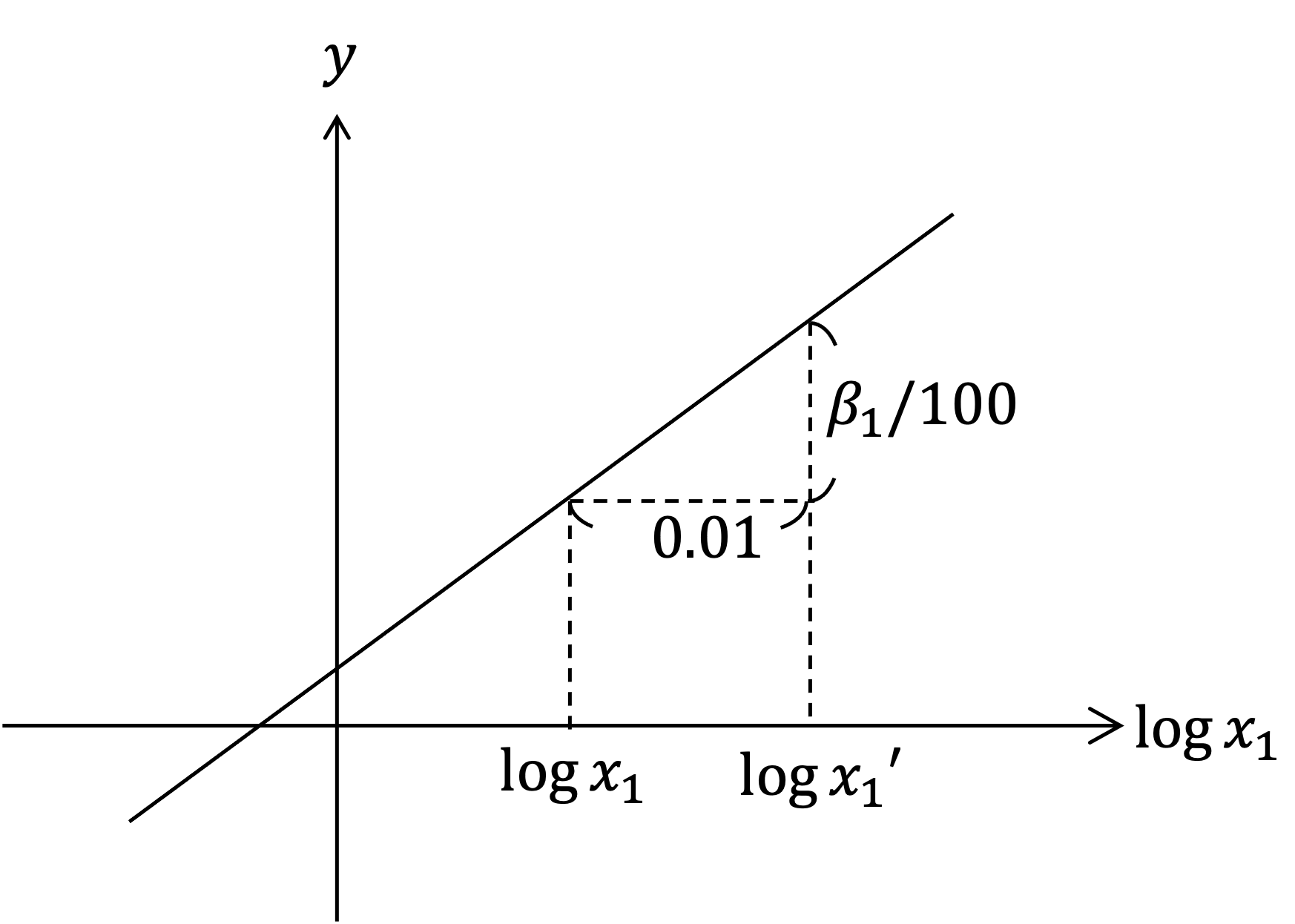
このモデルにおける$\beta_1$の解釈も,準備1での説明を直接適用すると「他の変数を一定として$\log x_1$のみを1増加させたとき,$y$は平均的に$\beta_1$だけ増加する」となります.次に,$\log x_1$の1の増加を0.01の増加に変えると「他の変数を一定として$\log x_1$のみを0.01増加させたとき,$y$は平均的に$\beta_1/100$だけ増加する」となります(上図参照).そして$\log x_1$の0.01の増加は,
\begin{align}
0.01 &= \log x' - \log x \\
&\approx {x' - x \over x}
\end{align}
と近似されるため,最終的に「他の変数を一定として$x_1$のみを1パーセント増加させたとき,$y$は平均的に約$\beta_1/100$だけ増加する」という解釈が可能になります.
説明変数と被説明変数の対数変換
最後に説明変数と被説明変数の両方を対数変換した以下のモデルを考えます.
$$
\log y_i = \beta_0 + \beta_1 \log x_{1i} + \dots + \beta_k x_{ki} + \varepsilon_i, \quad \varepsilon_i \overset{\mathrm{iid}}{\sim} (0,\sigma^2), \quad i = 1,\dots,n
$$
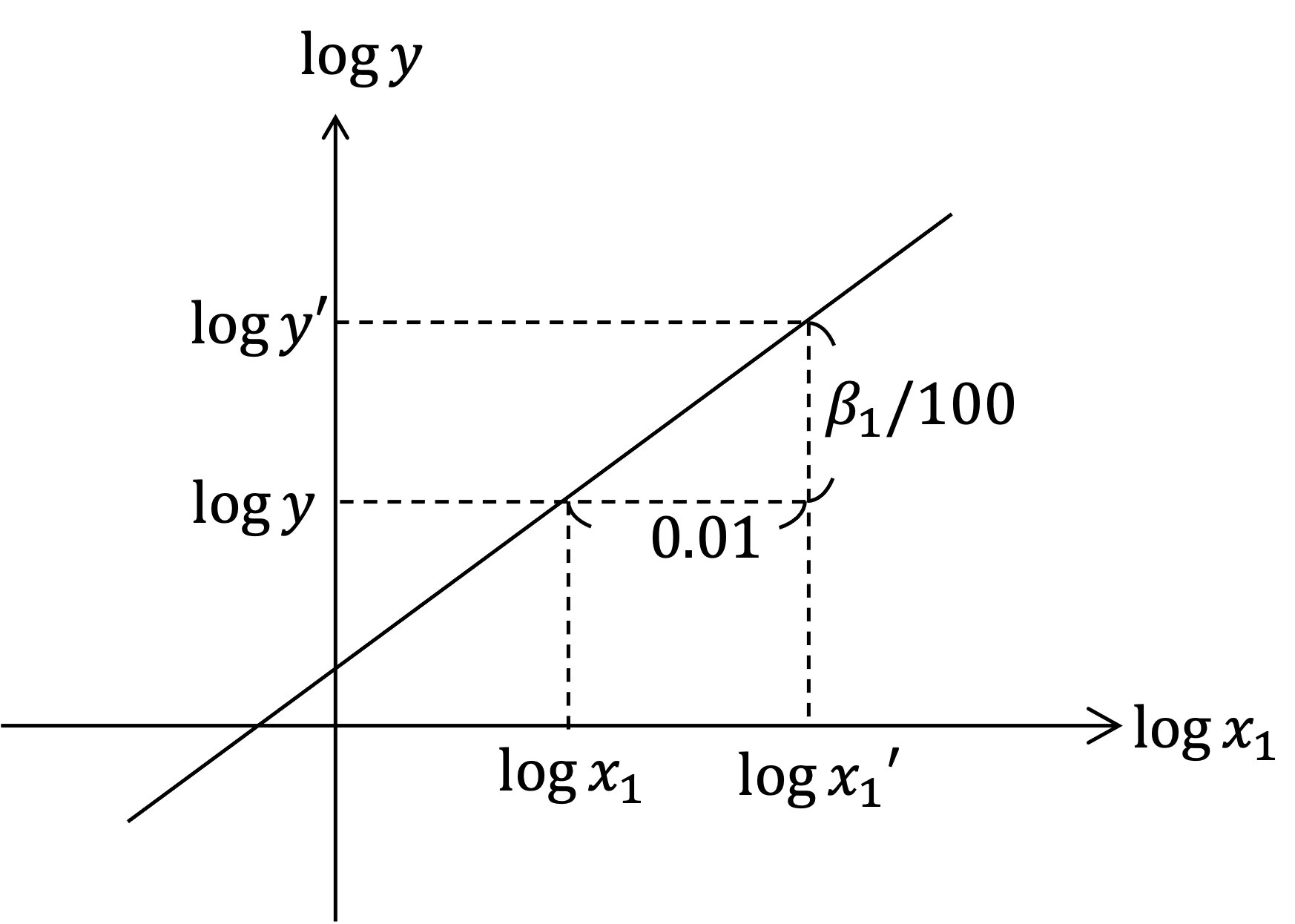
まず「他の変数を一定として$\log x_1$のみを0.01増加させたとき,$\log y$は平均的に$\beta_1/100$だけ増加する」という解釈からスタートします(上図参照).そして,$\log x$の$0.01$の増加は「$x$の約1パーセントの増加」を意味し,$\log y$の$\beta_1 / 100$だけの増加は「$y$の約$\beta_1$パーセントの増加」を意味するため,最終的に「他の変数を一定として$x_1$のみを1パーセント増加させたとき,$y$は平均的に約$\beta_1$パーセントだけ増加する」という解釈が可能になります.$\beta_1$はいわゆる弾力性の近似と解釈できます.
| $y$ | $\log y$ | |
|---|---|---|
| $x$ | $x$が1増えたとき,$y$は$\beta$増える | $x$が1増えたとき,$y$は$100\beta$%増える |
| $\log$ $x$ | $x$が1%増えたとき,$y$は$\beta / 100$増える | $x$が1%増えたとき,$y$は$\beta$%増える |
便利な回帰関数の形
多項式
線形回帰の枠組みの中でも,説明変数と被説明変数の非線形な関係性を表現することはできます.前節で説明した変数の対数変換もその1つですが,他に説明変数の冪乗を新しい説明変数として加えることで,回帰関数を多項式にすることができます.
$$
y_i = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \varepsilon_i, \quad \varepsilon_i \overset{\mathrm{iid}}{\sim}(0,\sigma^2), \quad i = 1,\dots,n
$$
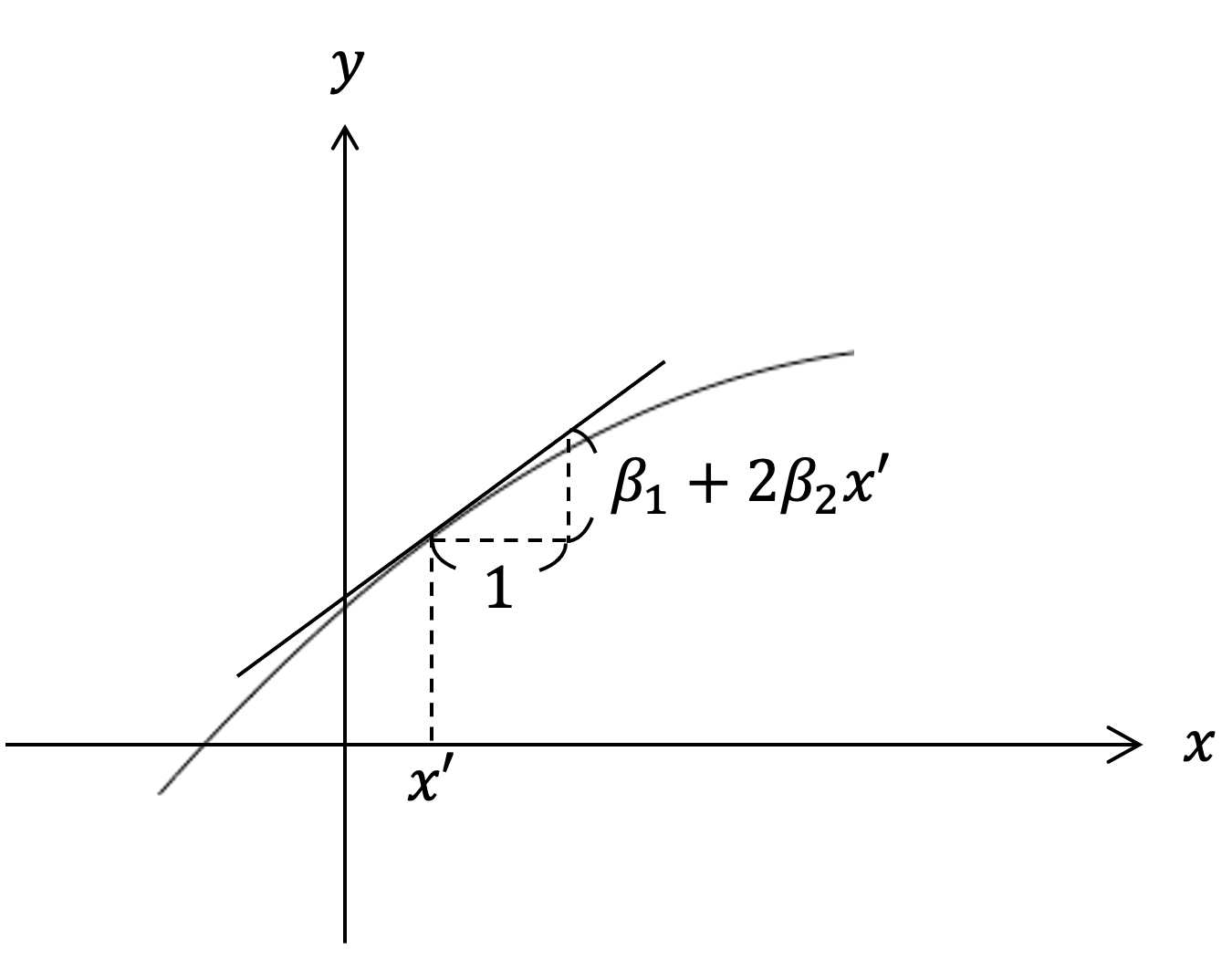
上のモデルは$x$と$y$の関係が2次関数の形で非線形になっているモデルです.$y$を$x$で微分すると,
$$
{\partial y \over \partial x} = \beta_1 + 2\beta_2 x
$$
となります(下図参照).よって「$x$を1増加させると,$y$は平均的に約$\beta_1 + 2\beta_2x$だけ増加する」と解釈され,$x$の変化の$y$に対する影響の大きさは$x$の値によって違います.場合によっては$y$への影響が正負逆になることもあります.例えば所得を勤続年数に回帰した場合,勤続年数が小さいところでの追加的な勤続年数は所得を増加させる効果があっても,その効果はだんだん小さくなり,ある年数からは所得を減少させる効果を持つ,ということは自然に考えられます.
交互作用項
英語ではinteraction termといいます.次のようなモデルを考えます.
$$
y_i = \beta_0 + \beta_1 x_i + \beta_2 z_i + \beta_3 x_i z_i + \varepsilon_i, \quad \varepsilon_i \overset{\mathrm{iid}}{\sim} (0,\sigma^2), \quad i = 1,\dots,n
$$
$x$が連続変数のとき,
$$
{\partial y \over \partial x} = \beta_1 + \beta_3 z
$$
より,「$x$が1増加させると,$y$は平均的に$\beta_1 + \beta_3 z$増加する」と解釈できます.$x$の$y$に対する効果の大きさは,$z$の大きさにも依存するということです.例えば$y$が所得,$x$が勤続年数,$z$が教育年数を表し,$\beta_1$と$\beta_3$がともに正の値で推定されたとします.このとき,勤続年数が1年長くなると所得も平均的に増えるが,その増え方は教育年数が長い方が大きいということが推測されます.
次に$x$がダミー変数のケースを考えます.$x_1 = 1$のとき,
$$
y_i = (\beta_0 + \beta_1) + (\beta_2 + \beta_3)z_i + \varepsilon_i,
$$
$x_i = 0$のとき
$$
y_i = \beta_0 + \beta_2z_i + \varepsilon_i
$$
とモデルは書き直せます.つまりダミー変数$x$によって分かれるカテゴリー間で,切片だけでなく傾きも両方変わるモデルが交互作用項によって表現されます.
おわりに
株式会社Nospareには,統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospare までお問い合わせください.
