はじめに
千葉大学・株式会社Nospareの川久保です.今日は初学者向けの内容になりますが,私が学部学生に統計学を教えているなかで,多くの学生がつまずく(もしくはつまずいていることにすら気づかない)と感じている箇所について,記事を書いてみようと思いました.
標本平均$\bar{X}$が母平均$\mu$の不偏推定量になる,つまり
$$
E[\bar{X}] = \mu, \tag{1}
$$
ということはどのような統計学の入門書にも書かれているかと思います.この証明を追うこと自体はそれほど難しくなく,特に数学に苦手意識がない人ほどすんなり受け入れてしまうものではないでしょうか.しかし,慎重な学生は「そもそも$\bar{X}$が確率変数ってどういうこと?」「標本平均の平均(期待値)って,あれ?何について平均とってるの?」と考え込んでしまいます.
問題設定
(1)式を示す上での問題設定は,
$$
X_1,\dots,X_n \overset{\textrm{iid}}{\sim} (\mu, \sigma^2)
$$
つまり,$X_1,\dots,X_n$が独立同一に,平均$\mu$,分散$\sigma^2$のある確率分布にしたがい,標本平均は,
$$
\bar{X} = {1 \over n}\sum_{i=1}^n X_i
$$
で定義されます.例として2021年6月の家計調査による食費のサンプル(標本)を考えます.このとき$X_i$とは,2021年6月の家計調査で,$i$番目の標本(実用上は標本の順番は関係ありませんが)として抽出される家計の食費のをあらわす確率変数と解釈できます.この$X_i$が確率変数であるのは,$i$番目のサンプルとして,どの家計が選ばれるか分からないからです.つまり母集団の確率分布において,分布の真ん中あたりなのか(平均的な食費の家計が選ばれるのか),分布の左裾の方なのか(平均よりもかなり小さい食費の家計が選ばれるのか),はたまた分布の右裾の方なのか(平均よりもかなり大きい食費の家計が選ばれるのか),家計調査が実施されるまでは分からない(randomである)ということです.それぞれの$X_i$について,どの家計が家計調査のサンプルとして抽出されるか分からないrandomnessをもつことから,それらの平均$\bar{X}$についてもrandomである(確率変数である)ということです.
不偏性
では標本平均$\bar{X}$が$\mu$の不偏推定量であるというのは,どういうことでしょうか.この不偏性は,数式で記述すると(1)式ですが,(1)式における期待値$E[\cdot]$は母集団の平均$\mu$,分散$\sigma^2$の確率分布についてとるものです.つまり「家計調査でどの家計が標本として選ばれるか,というrandomnessについて平均をとる」ということです.もっとくだけた表現をすると,「無限個のパラレルワールドで2021年6月の家計調査がたくさん行われ,それぞれのパラレルワールドでは異なる家計がサンプルとして抽出されるため異なる$\bar{X}$の値が実現するが,これら無限個の$\bar{X}$の実現値を平均すると(無限個の平均という考え方が初等確率ではもはや考えることができないのですが)母平均$\mu$と等しくなる」ということです.しかし実際の家計調査は1回しか行われないため,不偏性自体がどれくらい重要な概念なのかは議論の余地があります.さて,このことを理解するには,パラレルワールドを俯瞰できる神様になって,コンピュータでシミュレーションを行うのが1番かと思います.
mu <- 10 # 母平均
sigma2 <- 1 # 母分散
R <- 10000 # パラレルワールドの数
n <- 1000 # サンプルサイズ
Xbar <- numeric(R)
for(r in 1:R){
x <- rnorm(n, mean = mu, sd = sqrt(sigma2)) # サンプルサイズnの標本抽出
Xbar[r] <- mean(x) # 標本平均の計算と値の格納
}
上のようなRコードを実行すると,たしかに標本平均の数値的な不偏性が(おおよそですが)確認できるかと思います.上のRコードにおいて,forループの1つ1つにおけるxの発生が,それぞれのパラレルワールドにおける家計調査のサンプルの抽出に対応します.本当は無限個のパラレルワールドを考える必要がありますが,シミュレーションでは扱うことができないため,10000個のパラレルワールドを考えます.10000個の標本平均の値はベクトルXbarに格納されていて,この平均を計算することが,$\bar{X}$の期待値を求めることに対応します.
> mean(Xbar)
[1] 10.00024
muの値10と限りなく近くなり,不偏性が数値的に確認できたと言えるでしょう.
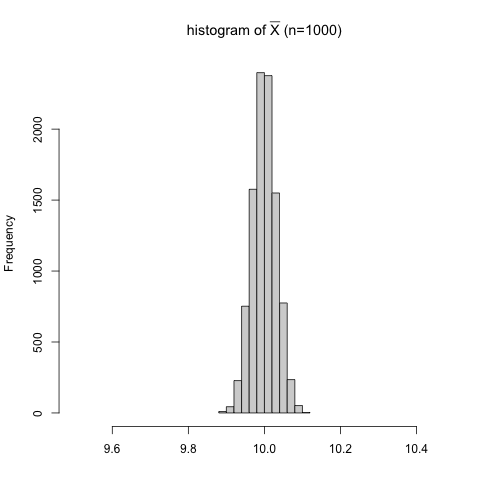
また,$\bar{X}$の分散は$V(\bar{X}) = \sigma^2 / n$であり,サンプルサイズ$n$に反比例します.つまり,サンプルサイズが大きいほど,異なるサンプルが抽出されたときに計算される$\bar{X}$の値のブレが小さいということを意味します.この事実は,nの値を変えた設定で実験を行い,Xbarのヒストグラムを描いてみると一目瞭然です.
信頼区間の意味
例えば頻度論的な$\mu$の95パーセント信頼区間が$[40,60]$と提示されたとき,その解釈として「真の平均$\mu$が40から60の間に入っている確率が95パーセント」とざっくり言ってしまいがちですが,これは厳密には誤りです.それはここまで説明してきた$\bar{X}$のrandomnessの意味を考えれば分かります.母集団の確率分布として正規分布$\mathrm{N}(\mu,\sigma^2)$,母分散$\sigma^2$が既知のもとでの信頼区間の導出は,$E[\bar{X}] = \mu, V(\bar{X}) = \sigma^2 / n$より,$\bar{X}$を標準化して,
$$
{\bar{X} - \mu \over \sqrt{\sigma^2 / n}} \sim \mathrm{N}(0,1)
$$
となることを用います.
\begin{align}
0.95 &\approx P\left( -1.96 \leq {\bar{X} - \mu \over \sqrt{\sigma^2 / n}} \leq 1.96 \right) \\
&= P \left( \bar{X} - 1.96\sqrt{\sigma^2 / n} \leq \mu \leq \bar{X} + 1.96\sqrt{\sigma^2 / n} \right)
\end{align}
という式変形から,$\mu$の95パーセント信頼区間は$[ \bar{X} - 1.96\sqrt{\sigma^2 / n}, \bar{X} + 1.96\sqrt{\sigma^2 / n} ]$と求まります.通常,$\bar{X}$にデータから計算した実現値を代入して数値として区間を$[40,60]$のように提示するわけですが,ここで気をつけなければならないのは,異なるパラレルワールドで別の標本が抽出されると,信頼区間の値が変わるということです.つまり信頼係数0.95の意味は「それぞれのパラレルワールドで計算された信頼区間が母平均を含んでいる確率が0.95である」ということであって「今手元にあるデータから計算した信頼区間に母平均が含まれている確率が0.95である」わけではありません.今手元にあるデータについてのパラメータの推論を行うという考え方は,データを所与としたパラメータの条件付分布にもとづいて推論を行うベイズ推論の信用区間がその立場をとっています.頻度論的な信頼区間の意味を理解するには,やはりパラレルワールドを複数観測できる神様の立場になって,シミュレーションを行うのが1番だと思います.
mu <- 10 # 母平均
sigma2 <- 1 # 母分散
R <- 10000 # パラレルワールドの数
n <- 1000 # サンプルサイズ
ct <- 0 # 信頼区間が母平均を含んでいるパラレルワールドの個数をカウントする変数
for(r in 1:R){
x <- rnorm(n, mean = mu, sd = sqrt(sigma2)) # 標本抽出
xbar <- mean(x)
L <- xbar - qnorm(0.975)*sqrt(sigma2 / n) # 信頼区間の左端点
U <- xbar + qnorm(0.975)*sqrt(sigma2 / n) # 信頼区間の右端点
if((L < mu) & (mu < U)){
ct <- ct + 1
}
}
10000個のパラレルワールドのうち,信頼区間が母平均を含んでいる世界の割合は,
> ct / R
[1] 0.956
と計算され,信頼係数0.95に近い値と言えるでしょう.
おまけ
まれに「実世界の母集団は有限なんだから,$X_1,\dots,X_n$が互いに独立というのはおかしいのではないか」と質問してくる鋭い学生がいます.非復元単純無作為抽出という実世界で最も基本的な標本抽出の方法で考えた場合,その主張は正しいです.それは母集団が有限だから,ということと,非復元抽出だから,という理由です.非復元ということは「1度取り出したボールを箱の中に戻さない」ということで,つまり$n$個のサンプルの中にダブりは存在しないということです.このような**有限母集団(finite population)**の解析には,母集団の値が$x_1,\dots,x_N$(ここで$N$はサンプルサイズでなく,母集団サイズ),個々のunit(家計,個人)が標本として選ばれれば1,選ばれなければ0をとる確率変数を$Z_1,\dots,Z_N$という記法を導入するのが便利です.このとき標本平均は
$$
{1 \over N}\sum_{i=1}^N x_iZ_i, \tag{2}
$$
と書くことができ,randomnessは,どのunitがサンプルとして抽出されるかを表す$Z_i$のみに依存し,$x_1,\dots,x_N$を定数と考えます.ここで$Z_1,\dots,Z_N$は独立ではなく,例えば$Z_i = 1$を所与とした($i$番目のunitが標本として選ばれたことを知っているとき),$Z_j = 1 \ (j\not= i)$の条件付確率は,
$$
P(Z_j = 1 \mid Z_i = 1) = {n-1 \over N-1}
$$
となります.これは$j$番目のunitがサンプルとして選ばれたのだから,残り$(N-1)$個のunitの中から$(n-1)$個を等確率で選ぶためです.このような$Z_1,\dots,Z_N$の確率分布に気をつけて,(2)式の平均(期待値)と分散を計算すると,不偏性は変わらず成り立っても,分散は少し小さくなります.
さらに,$x_1,\dots,x_N$を定数とするのではなく,$x_1,\dots,x_N$に確率モデルを仮定し,有限母集団はそのモデルからの実現値であり,実際に観測されるのはサンプルサイズ$n$の標本抽出による一部である,とする考え方もあります.$x_1,\dots,x_N$を生成する確率モデルのことを,**超母集団(super-population)**といい,超母集団の未知パラメータを推定した後,有限母集団の未観測の値を予測することで,様々な有限母集団パラメータ(平均,分散,分位点など)を予測する手法もしばしば用いられます.この1つが以前の記事で紹介した個票レベルモデルの小地域推定で,超母集団に補助変数への回帰モデルを仮定することで,補助変数を通したより有効な予測ができるのが利点になります.
まとめ
株式会社Nospareには,統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospare までお問い合わせください.