はじめに
こんにちは、今回は最近たまたま知って論文読んでたTopological Data Analysisについて書こうと思います。数学的なところはだいぶはしょって書きます(めんどくさい)。備忘録的なやつです、間違ってるところあったらごめんなさい。
TDAとは
TDAは、幾何学的な観点からデータの解析を行う手法です。幾何学を用いる解析として「情報幾何学」が有名ですが、TDAではトポロジー(位相幾何学)という学問を用いて解析を進めます。では、トポロジーとは一体なんなんでしょうか。
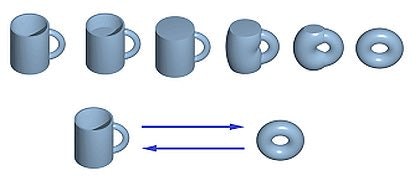
トポロジーには、「伸縮したり連続的に変形させた図形は同じとみなす」という特徴があります。以下の図を見てください。
人間の目にはこの3つの図形は明らかに違う図形に見えます。しかしトポロジーの世界ではこれらの図形は同じです(同型である、と言います)。では逆にどういう図形がこれらの図形と「違う」図形なんでしょうか?
以上の3つの図形は先ほどの図形とは異なる図形です。なぜなら、先ほどの図形をどのように変形しても、(穴を開けたりしない限り)上の図形のようにすることはできません。すっっごい簡単にいうと、繋がり方が同じで穴の数が同じだったら同型です。有名なのはコーヒーカップとドーナツが同じ形ってやつですね。
まあすんごい無理やりな変形してる気もしますが、数学的に正しい話です。
では、こんなある意味直感と反することを考えて何の利点があるのでしょうか?
以下の図形を見てください。
以上の図はフォントの異なる"ANALYSIS"という文字列です。これらを文字認識するとなった時、人間の目から見れば明らかですが、機械に判断させるとなると難しいかもしれません(これくらいなら行けそうな気もしますが)。こういう時にトポロジーは役に立ちます。「図形の穴の数」で文字を分類すれば、多少字が崩れていても問題なく分類できます。
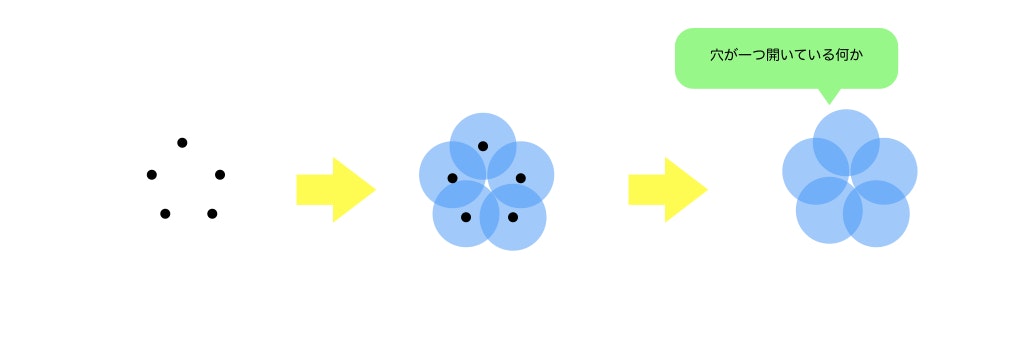
では、具体的にトポロジーをどのようにしてデータ解析に応用するのでしょうか?まずデータとしてサンプル点がいくつかプロットしてあったとします(下図左)。通常ならここから線形回帰などで解析を進めていくのですが、ここからTDAでは各点を中心として球を書きます。半径を徐々に大きくしていくと、そのうち球同士が重なるようになります。この時、球同士の間に小さい隙間(穴)が生まれます。また、ここから半径をさらに大きくするといつか穴が潰れて無くなります。このようなプロセスから情報を引き出して解析するのがTDAです(ちなみに穴が生まれることを「生成」、穴が潰れることを「消滅」と言います)。ですが、この図形をコンピューターが読み取るのは正直難しいです。ここで、TDAでは「抽象単体複体」というものを読み取ります。とりあえずこれの定義をしましょう(疲れた)。
単体、複体とは
まず単体について述べます。だいぶ数学的な話になるのですが、詳しくは数学書に任せるとして、ここではふんわり定義します。単体というのは、0次元の点、1次元の線分、2次元の三角形、3次元の四面体、4次元の五胞体といった概念の一般化です。また、単体はそれより次元の低い単体をそれ自体に含むのですが、これを「面」と呼びます(例えば、三角形は線分を3つ含み、四面体は三角形を4つ含みます)。
また、有限個の単体の集合 $K$ が条件
- $a ∈ K$ かつ $c$ が $a$ の面 $=>$ $c ∈ K$
- $a, b ∈ K$ かつ $a ∩ b ≠ 0$ => $a ∩ b$ は $a$ の面かつ $b$ の面
を満たす時、Kを単体的複体と言います。
図形を単体的複体として、図形としてではなく単体の集合として見ることでコンピューターを使った解析が楽になります。
パーシステントホモロジーについて
TDAでは、前述した単体的複体として得た情報を用いて、「パーシステントホモロジー」と呼ばれるアルゴリズムで解析します。
これを考えるために、サンプル点としてノイズ()を含むデータを考えます。(下図)
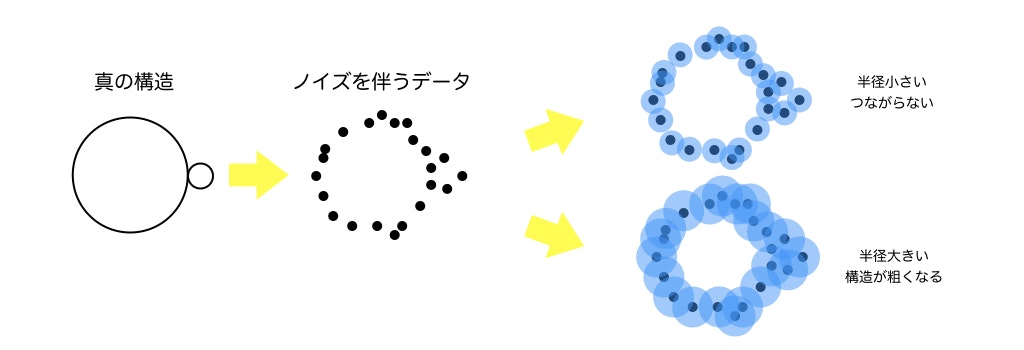
この状態で球の半径を大きくしすぎると小さい構造が潰れてしまい、小さくしすぎると大きい構造が繋がらない、という問題が発生します。この時、どのようにして構造を決定すればいいのでしょうか。ここで用いるのが「パーシステントホモロジー」です。
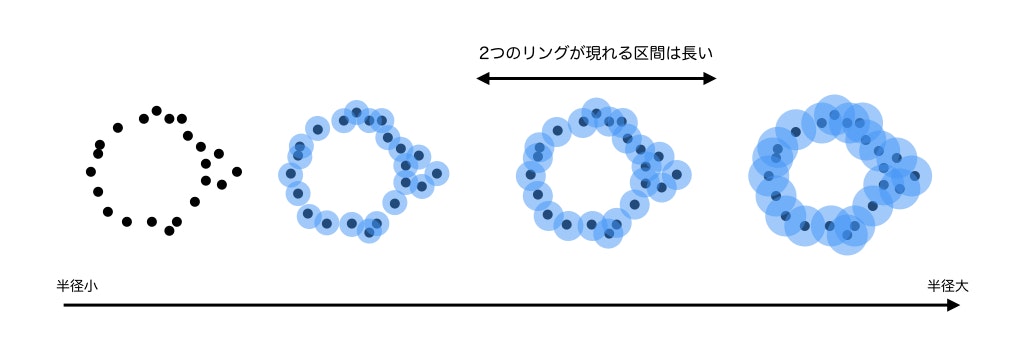
このアルゴリズムでは、球の半径を徐々に大きくしていって、「どの構造が長く現れるか」、という区間を計算します。もっとも長く現れる区間の構造をデータの構造として決定する、というのがパーシステントホモロジーです(安定した構造を発見する)。また、TDAは高次元のデータにも適用できるため、構造を視覚的には捉えることのできないデータの位相的構造を決定することができます(もちろんデータには位相的構造は仮定しますが)。
高次元のデータを可視化するアルゴリズムとしてPCAなどの次元圧縮が挙げられますが、それらのアルゴリズムではデータの多様体的性質や、表面が滑らかであることなどを仮定しています。TDAの利点はデータにこれらの性質を仮定しないことです。よってTDAは幅広いデータに適応できます。
終わりに
今回はTopological Data Analysisについてすごくざっくり説明しました。とても興味深い手法だと思うのでデータ解析に使っていきたいと思います。
参考文献
1.http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.440.3587&rep=rep1&type=pdf
Afra Zomorodianさんの"Topological Data Analysis"