因子分析の理論とPythonでの実装

はじめに

初めまして、コジコジと申します〜。
20歳で学生やってます、大学では数学の勉強やってます。
最近は主に機械学習の勉強をしています、進捗のまとめしたいと唐突に思い立って初投稿です笑

さて、初投稿ということで、ちょうど今日本読んで出てきた因子分析のことにしようと思います。拙い文章ですが、よろしくお願いします。

因子分析とは

前置きはここまでにして、本題に入ろうと思います。
因子分析というのは、簡単にいえば「いくつかのデータの関係性を少ない情報量で表してグループ分けする」手法です。簡単な例で見てみましょう。

相関行列

	国語	英語	社会	化学	物理	数学
国語		.7	.69	.03	-.9	.34
英語	.7		.53	-.14	-.33	.06
社会	.69	.53		.11	.06	.38
化学	.03	-.14	.11		.57	.46
物理	-.09	-.33	.06	.57		.66
数学	.34	.08	.38	.46	.66

上の行列は相関行列というものです。各セルには-1から1の範囲の数が入っていて、一つ一つを相関係数といいます。この数字は2つの教科の関係性を表しています。例えば、英語と国語に当たるセルを見てみると、0.7という比較的大きめの数が入っています。これは、「英語の点数が高い生徒は国語も高い傾向にある」ということを表しています。
では国語と物理のセルを見てみましょう。数字は-0.9でかなり小さいですね。これは「国語の点数が高い生徒は物理はできない傾向にある」ということを表しています。
理系ですね（は?）

とまあこの通り、この表をちょっと眺めてみると、「理系科目できるやつは文系科目できない」、逆に「理系科目できるやつは文系科目できない」という傾向があるということが何となく分かります。現実では知らないです、はい。
このことから、この６科目はn
何となく「文系科目」と「理系科目」に分類できるということがわかります。

因子分析

上で説明した通り、相関行列見れば何となく「理系科目」と「文系科目」に分類はできます。でも、上の行列だと数字多くてなんか見づらいですよね。そんな時に役に立つのが因子分析です。
因子分析を行うと以下のような行列ができます。

	I	II
国語	.9	.2
英語	.8	-.1
社会	.7	.3
化学	-.1	.6
物理	-.3	.9
数学	.2	.8

おお、数字が少ない！これなら見やすそうですね。こんな少ない数字でも教科の関係性を表せています。
まず、Iの行をみると先ほどの「文系科目」の数字が大きく、「理系科目」の数字が小さいことがわかります。IIの方では逆ですね。このI、IIのことを因子負荷数って言ったりします。
このように、因子分析を行うと相関行列の次元を小さくできます。要するに次元削減ってやつですね、PCAとかで有名なアレです。

さて、じゃあどうやって次元削減してるかってことなんですけど、ちょっと初投稿で疲れてきたんで割愛ってことで（本音はめんどくさい）。割とめんどくさい計算してるですけど、気が向いたらまた書きます笑

Pythonでの実装

では、因子分析をPythonで実装してみましょう。本当はこういう統計解析的なのはRの方がいいみたいなんですけど、調べたらsklearnにモデルあったのでとりあえずPythonで。ついでにPCAと結果を比較してみます。
データセットは、みんな大好きIrisデータを使いましょう。

# 必要なものをimport
from sklearn import datasets
import numpy as np
from sklearn.decomposition import FactorAnalysis
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA


# irisデータをロード
iris = datasets.load_iris()
y = iris.target


#　変換器を作成
pca = PCA(n_components=2)
fa = FactorAnalysis(n_components=2, max_iter=5000)
sc = StandardScaler()
transformers = [pca, fa]


# ２種類のプロットを実行する関数
def compare_plot():
    y = iris.target
    colors = ["red", "blue", "green"]
    fig, ax = plt.subplots(1, 2, figsize=(10, 4))
    for i in range(2):
        for j in np.unique(y):
            X = iris.data
            sc.fit_transform(X)
            X = transformers[i].fit_transform(X)
            ax[i].scatter(X[y==j, 0], X[y==j, 1],
                            color=colors[j])

 
# 処理を実行           
compare_plot()

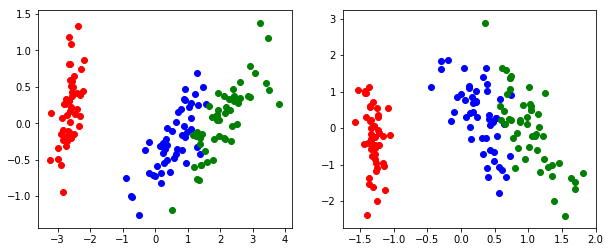
実行結果は以下です。
右のグラフがPCA、左が因子分析によるプロットです。

これは...どうなんでしょうか...？
この後で線形分離とかすること考えるとPCAの方がいい感じもしますね...

まとめ

初投稿は因子分析についてまとめましたが、変換器としての優秀さは用いるデータセットにもよるので一概には言えませんね。そういうのを見分けられるように精進していこうと思います。
気が向いたらちょこちょこ投稿すると思います。読んでいただきありがとうございました。