Frenet Frameによる軌道最適化を用いて障害物回避(WIP)

記事作成途中です．

目的

グローバルプランナーなどで与えられた目標trajectory（以降，center lineと呼ぶ）をもとに，障害物を避けるようなtrajectoryをいい感じに生成することを目的としています．イメージは以下の図のようなものです．

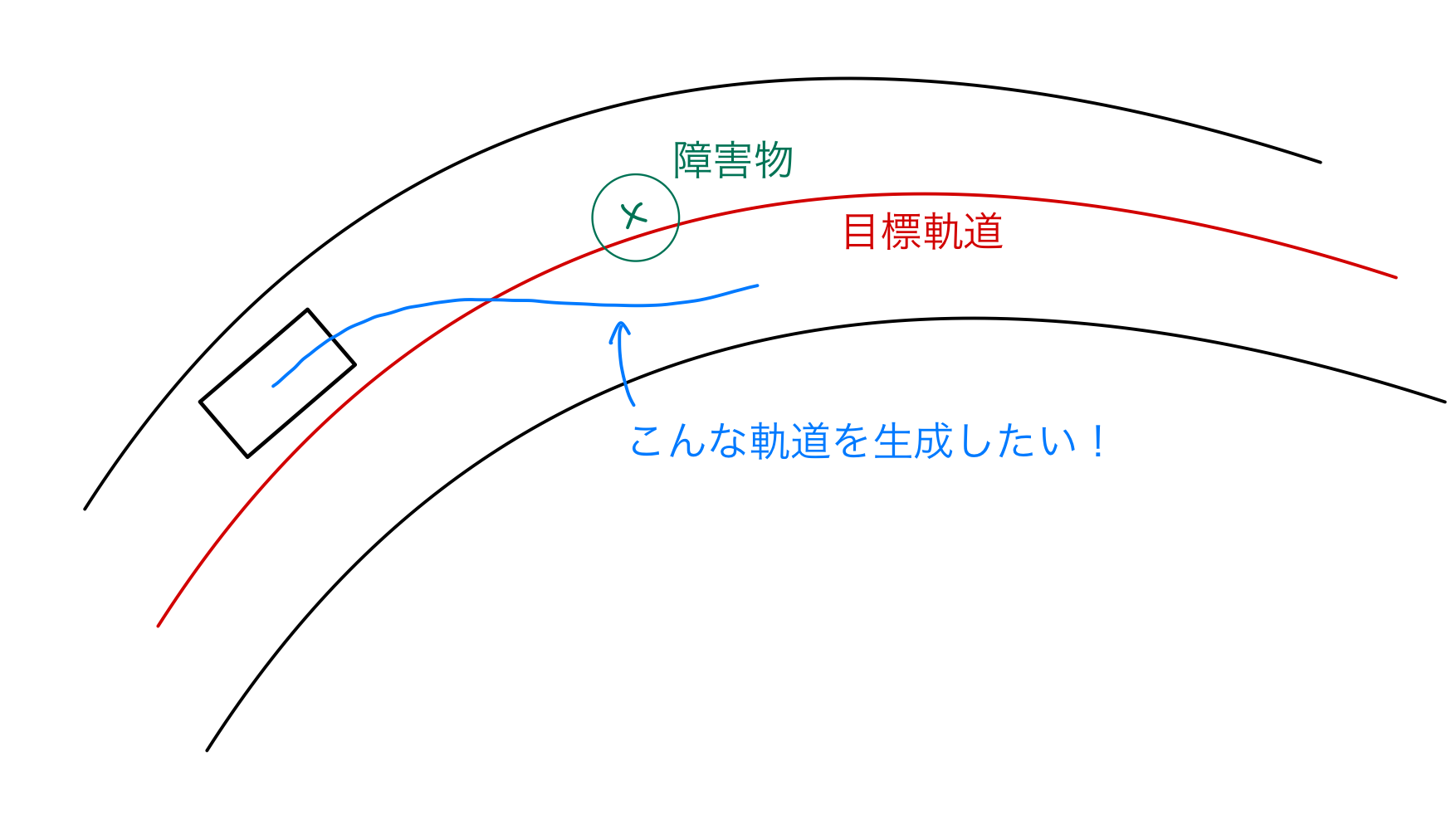
参考

この記事を書くにあたって以下の資料を参考にしました．

• 元論文 : Optimal Trajectory Generation for Dynamic Street Scenarios in a Frene´t Frame

• Python Robotics

  • Optimal Trajectory in a Frenet Frame [ドキュメント],[実装]
  • Quintic polynomials planning [ドキュメント],[実装]

• 記事 fjp.github.io : Trajectory Planning in the Frenet Space

Frenet座標系について

このアルゴリズムを理解するために重要な概念であるFrenet座標系について説明します．Frenet座標系とは，一言で表すと「center lineに沿った座標系」です．

一般的に座標系は以下のような$(x,y)$座標を考えます．
(fjp.github.ioより)

これに対してFrenet座標系は，center line(青線)を軸$s$とし，それに直交する線を軸$d$とする$(s,d)$座標を考えます．
(fjp.github.ioより)

trajectoryを計画する際には，最初はFrenet座標系でtrajectoryを考えて，それを直交座標系に戻すというアプローチをとります．

アルゴリズムの概観

以下のアニメーションは，実際にプランニングをしている様子を示しています．青がcenter lineで，赤が障害物を回避するように最適化されたtrajectoryを表しています．

(python roboticsより)

これらアルゴリズムは，以下のような手順を踏みます．

1. center lineを求める

   • このcenter lineは，Frenet座標系の$s$軸として用います．

2. Frenet座標系での最適化に用いる初期位置・速度・加速度を求める

   • 最初にプランニングを行う場合は，現在の直交座標系での状態からFrenet座標系の状態に変換する必要があります．それ以外の場合では，前回計算したtrajectoryの次の点を用います．(このアルゴリズムはMPCではないので，毎ステップ，観測された現在の状態からFrenet座標系での状態に変換する必要はありません．)

3. 横方向と縦方向のtrajectoryを計算する

   • 基本的に横方向のtrajectory$d(t)$と縦方向$s(t)$を独立に求めます．(車速が低速の場合は，この記述は当てはまりません．ここで詳細を説明します)
   • ここで求めるtrajectoryは，1つではなく，複数のtrajectoryを求めます．最終的に，これらのtrajectoryの中から，制約を満たした最も良いtrajectoryを選びます．
   • これら複数のtrajectoryは，一つの初期条件(状態) と，$s$や$d$や時間間隔$T$が異なる複数の終端条件(状態) を満たす多項式として表されます．
   • 以下が実際に生成されるFrenet座標系でのtrajectoryです．
     

4. 縦方向と横方向のtrajectoryを合わせる

   • ここは，特に難しいとこは無いのですが，$C_{\text {tot }}=$ $k_{\text {lat }} C_{\text {lat }}+k_{\text {lon }} C_{\text {lon }}$のように，横方向でのコスト$C_{\text {lat }}$と縦方向でのコスト$C_{\text {lon }}$に係数$k_{\text {lat }}, k_{\text {lon }}$を掛けて，トータルコスト$C_{\text {tot }}$を求めます．

5. 直交座標系でのtrajectoryを求める

6. 複数のtrajectoryの中から障害物に衝突せず，コスト$C_{\text {tot }}$が最も小さいtrajectoryを選択する

アルゴリズムの詳細(WIP)

center lineのプロパティ

center lineはFrenet座標系で求めた多項式で表されるtrajectoryから，直交座標系でのtrajectoryを求める必要があります．詳しくはFrenet座標系から直交座標系への変換に記述しますが，

• 最適化したtrajectoryとして，位置$\vec{x}$のみを求めたい場合，center lineはtrajectory上で進んだ距離$s$から，以下を求めることができる必要があります．
  • center line上の点$\vec{r}(s)$
  • center lineの傾き$\theta_{r}(s)$
• 最適化したtrajectoryとして，速度$v_x$や速度の向き$\theta_x$も求めたい場合，上記に加え，以下のものを求める必要があります．
  • center lineの曲率$\kappa_{r}(s)$
• 最適化したtrajectoryとして，曲率$\kappa_x$や加速度$a_x$も求めたい場合，更に以下を求めることが出来る必要があります．
  • center lineの曲率の変化率$\kappa_{r}'(s)$

横方向のプランニング

1. High Speed Trajectoryの場合

2. Low Speed Trajectoryの場合

縦方向のプランニング

Frenet座標系から直交座標系への変換

サンプルコードと実行結果(WIP)