線形回帰モデル
回帰問題
線形回帰モデルは教師あり学習
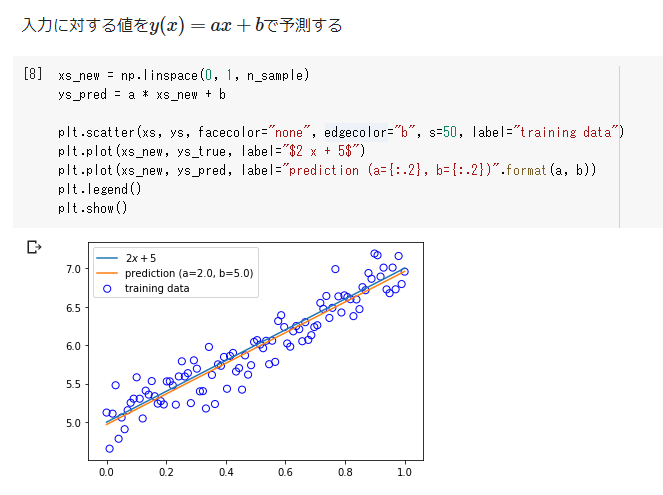
→直線 線形回帰
→曲線 非線形回帰
線形結合(入力とパラメータの内積)
→入力ベクトルと未知のパラメータの各要素を掛け算し足し合わせたもの
→入力した情報が多くても出力は１つ
線形回帰モデルのパラメータは最小二乗法で推定
→最小二乗法
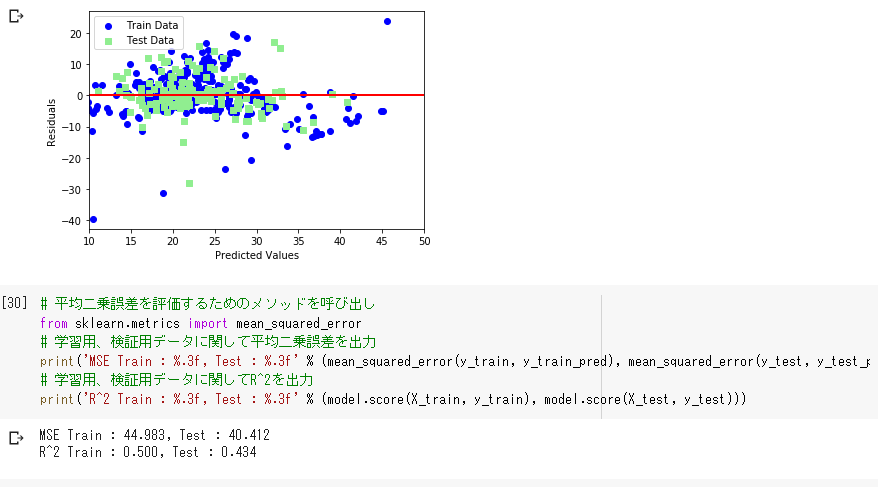
学習データの平均二乗誤差を最小とするパラメータを探索
学習データの平均二乗誤差の最小化は、その勾配が0になる点を求める
単回帰
→numpyでの実装とsklearnでの実装がある
ボストンの住宅価格予測
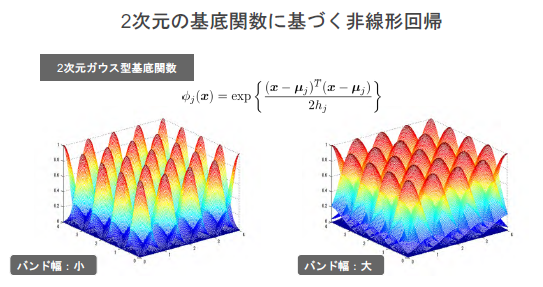
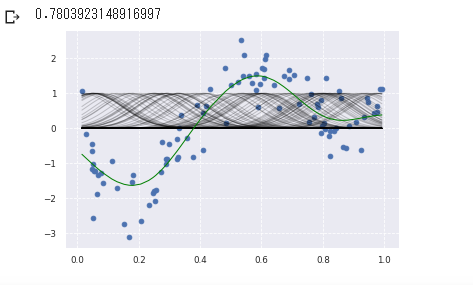
非線形回帰モデル
複雑な非線形構造を内在する現象に対して、非線形回帰モデリングを実施
→分母のhjが変化すると、バンド幅も変化する
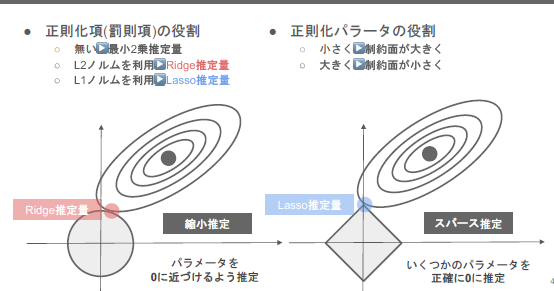
Rigde推定量 Lassso推定量
Rigde推定量・・・円が小さくなると、パラメーターが０になる割合が増える
原点付近に制約を当てて、MSEを最小にする点を見つける
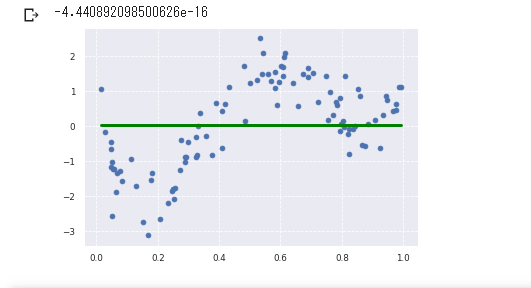
Lassso推定量・・・推定をする段階で不要な変数を排除する
◇の中でMSEが0になる点を見つける
ホールドアウト法
データを学習用とテスト用の2つに分割し、「予測精度」や「誤り率」を推定する為に使用
→分割の方法によっては、かたよりが生じてしまう
ロジスティック回帰モデル
分類問題(クラス分類)→ある入力(数値)からクラスに分類する問題
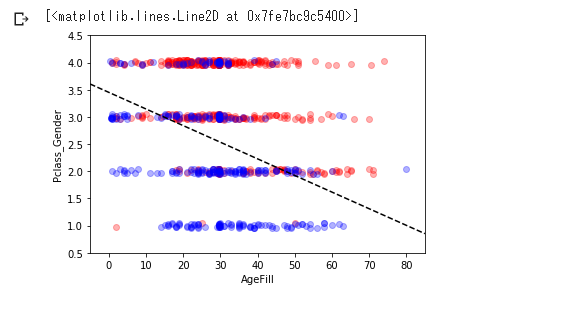
タイタニックの生存率
実装(チケット価格から生死を判別)
実装(2変数から生死を判別)
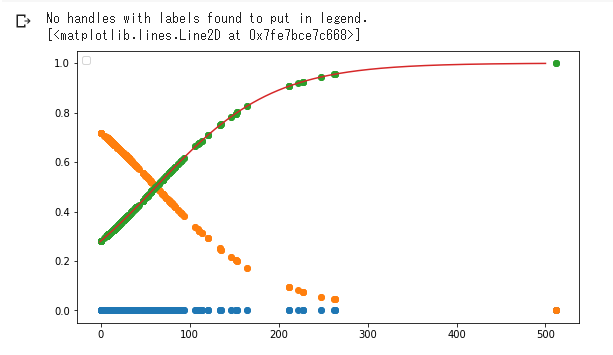
シグモイド関数
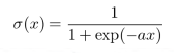
a=1の時のシグモイド関数を標準シグモイド関数という
aの値が大きくなるほど、変化の度合いは大きくなる
シグモイド関数は最適化問題に使用しやすい
最尤推定
分類の評価方法
→ラベルの数がインバランスの場合、正しい正解率にならない
主成分分析
次元圧縮時の情報のロスを少なくする
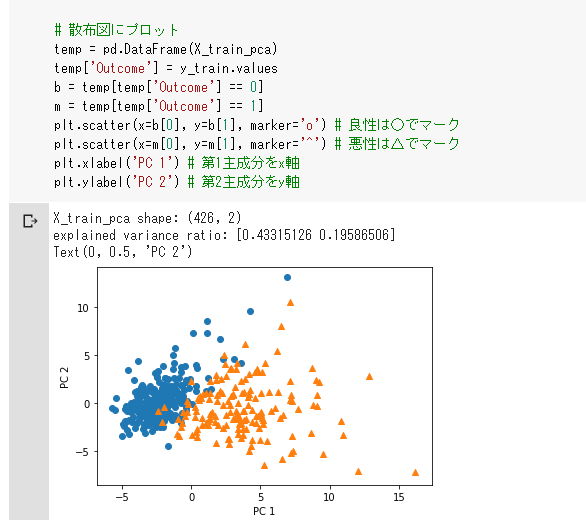
データの特徴を抽出し、高次元データを低次元にし可視化する
→aに関して、最大になる数を求める。その場合の最適化解は最適化問題を解いた際の解と一致する
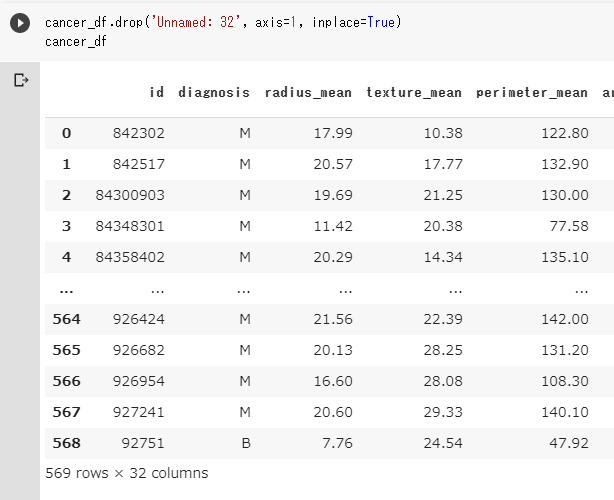
乳がんデータ分析
寄与率
→圧縮した結果、どれほど情報が減ったのか
複数次元のデータを使うことが大切
アルゴリズム
k近傍法
最近傍のデータを個取ってきて、それらがもっとも多く所属するクラスに識別
kを変化させると結果も変わり、kを大きくすると決定境界は滑らかになる
k-平均法(k-means)
教師無し
事前にクラスタの個数を指定する必要がある
中心の初期値を変えると、クラスタリングの結果も変わる
ワインデータセットを使用したk-means法
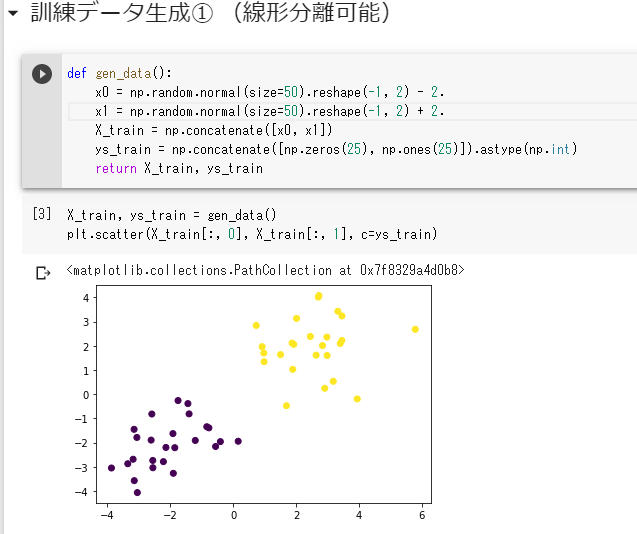
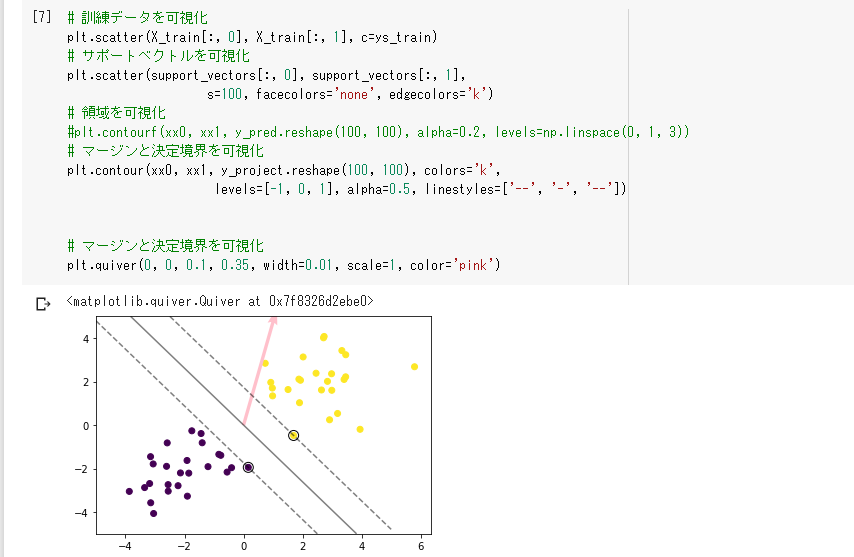
サポートベクターマシン
2クラス分類のための機械学習手法
予測
マージン
線形判別関数ともっとも近いデータ点との距離
目的関数
max M
サポートベクター
分離超平面を構成する学習データは、サポートベクターだけ。残りのデータは不要
ソフトマージンSVM
線形分離できない場合でも対応。
誤差を許容し、誤差に対してペナルティを与える
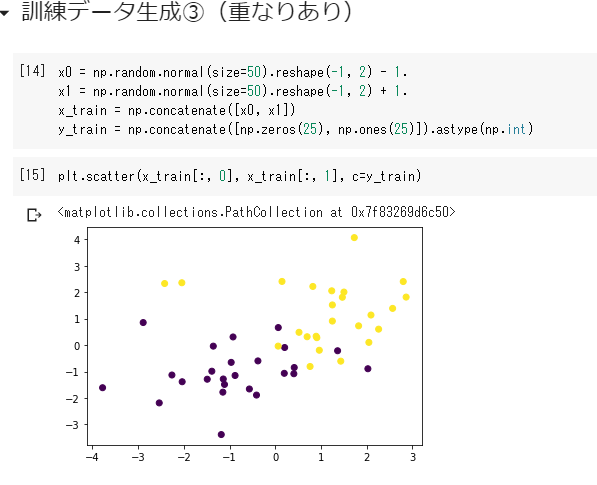
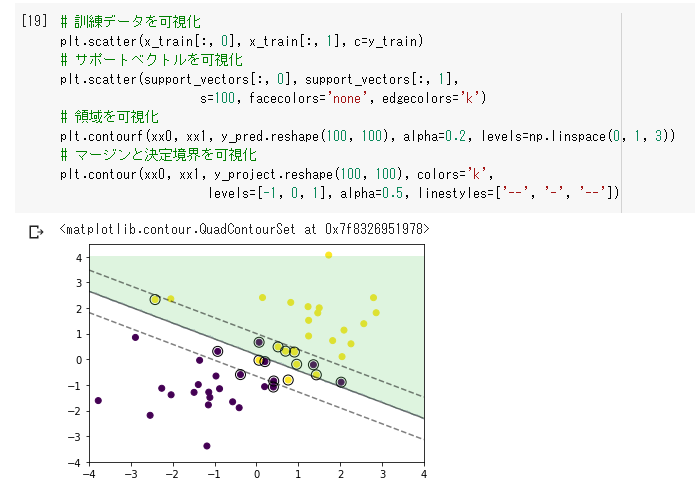
非線形分離
線形分離できないとき
特徴空間に写像し、その空間で線形に分離。元の空間上では非線形な分離