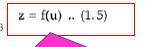###入力層～中間層
中間層は、隠れ層ともいう。
ニューラルネットワークは、層から層へ、値を変換していく。
層と層の間にあるノード間の結合は、一つ一つが重みを持っている。
総入力＝（重み×入力）の合計＋バイアス
Pythonでの入力：u1=np.dot(x,W1) + b1
→内積をとる際、数字をそろえる
→34 43
複数の項目を入力層にて入力し、次の層へ伝達
###活性化関数
中間層用の活性化関数
➡Z1 = function.sigmoid(u)
ステップ関数
→しきい値を超えたら発火する関数であり、 出力は常に１か０。
パーセプトロン（ニューラルネットワークの前身）で利用された。
→線形分離可能しか学習できない
ReLU関数
→今最も使われている活性化関数
勾配消失問題の回避とスパース化に貢献する
シグモイド（ロジスティック）関数
→0 ~ 1の間を緩やかに変化する関数
→勾配消失問題を引き起こすことがある
###出力層
誤差関数
→ある測定値が正規分布で与えられる場合に、その測定値が −aから aの範囲にある確率
➡誤差関数に平均二乗誤差を用いている
ソフトマックス関数
→ソフトマックス関数の出力は0~1の実数値に落とし込むことができる
出力層の活性化関数
・中間層： しきい値の前後で信号の強弱を調整
・出力層： 信号の大きさ（比率）はそのままに変換
→出力層と中間層で利用される活性化関数が異なる
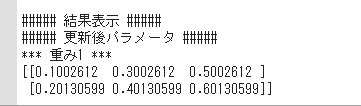
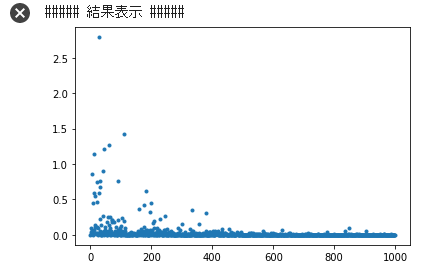
###勾配降下法
学習率の値によって、学習の効率が大きく異なる
学習率が大きすぎる場合：最小値にいつもでもたどり着かず発散
学習率が小さい場合：小さすぎると収束に時間がかかる
普通の勾配降下法のことをバッチ勾配降下法といい、確率的勾配降下法のことをオンライン勾配降下法ということがある。
###誤差逆伝播法
算出された誤差を、出力層側から順に微分し、前の層前の層へと伝播。
教師データと実際と出力データとの間に生じる誤差情報を使ってネットワーク全体を学習する。
最小限の計算で各パラメータでの微分値を解析的に計算する手法
