最適な成長スケジュール 〜なぜ秋は美味しいのか？〜

はじめに

この記事は，東京大学理学部物理学科の有志による 理物 Advent Calendar 2022 の3日目の記事です．

昨年度 Physics Lab. 2022 Advent Calendar 2021 に参加したのですが，今年度は B4 も書いて良いとのことなので，1日分だけ枠を頂戴することにしました（後日見てみたら B4 私しかいないが）．

突然ですが，今セメスター受講している講義「進化生態学」（生物学科）がなかなか面白いです．そこで登場する「成長スケジュール」の話を簡単に紹介しようと思います．講義では生物寄りの話が多く，モデルの詳細な計算などは省かれてしまっていたので，それらを簡単にまとめます．詳しい計算（Pontryagin の最大原理を使った計算）を追いたくない人はスキップできるような構成にしようと思うので，ぜひ最後までスクロールして眺めてみてください．

成長スケジュール

栄養成長と繁殖成長

光合成をする植物を考えましょう．
植物は光合成産物を使って成長しますが，この際どの部分を成長させるかという自由度があります．葉・茎・根などの 栄養体 を作る成長を 栄養成長 といい，花・実・種子など子孫を残すための 繁殖体 を作る成長を 繁殖成長 といいます．栄養成長と繁殖成長はトレードオフの関係になっており，成長のどの程度を栄養成長／繁殖成長に割くのかということは，植物の戦略としてとても重要です．植物を含むすべての生物の目的は「子孫を多く残す」ということにあるので，繁殖体を多く残すことが植物のミッションになります．

モデルを考える前に，直感的な考察をしてみましょう．
まず「繁殖体を多く残すことが目的なのだから光合成産物をすべて繁殖成長にまわそう！」と考えたくなりますが，実はこれは非効率です．光合成をするためには葉（栄養体）が必要で，葉（栄養体）が多ければ多いほど得られる光合成産物は多くなります．つまり，栄養体をあらかじめ大きくしておけば，次の段階で得られる光合成産物が多くなります．

たとえば，栄養体 "1" につき光合成産物が "2" だけ得られる状況を考えましょう．はじめに "1" だけの栄養体（種子）があったとして，光合成産物が "2" 得られたとします．これを繁殖成長にまわすと，次の段階で得られる光合成産物は同じく "2" です．以降すべてを繁殖成長にまわす場合には，得られる光合成産物は常に "2" で，$n$ 段階後の繁殖体は "$2n$" になります．

表１：繁殖成長のみをし続けた場合

段階	0	~	1	~	2	~	3	~	4	~	5	~	6
栄養体	1		1		1		1		1		1		1
繁殖体	0		2		4		6		8		10		12
光合成産物		2		2		2		2		2		2

一方で，はじめに栄養成長にまわすと，栄養体は "2" となり，それによって光合成産物を "2" 得ることができます．さらにそれを栄養成長にまわせば光合成産物を "4" 得ることができます．これを繰り返せば各段階で得られる光合成産物は "1", "2", "4", "8", "16", … のように指数関数的に増えて行くことがわかるでしょう．$n-1$ 段階目までは栄養成長を続け，$n$段階目で初めて繁殖成長をしたときの繁殖体は "$2^{n-1}$" となります．

表2：栄養成長を続け，最後に繁殖成長をした場合

段階	0	~	1	~	2	~	3	~	4	~	5	~	6
栄養体	1		3		9		27		81		243		243
繁殖体	0		0		0		0		0		0		486
光合成産物		2		6		18		54		162		486

ここで見た簡単な例のように，最終的な繁殖体を最大にするためには，最初は栄養成長を続け，途中から繁殖成長を始めるのが良さそうです．では繁殖体を最大にするためには，どのタイミングで繁殖成長を始めて，どの程度の光合成産物を繁殖成長に割けば良いのでしょうか？　次の節で簡単なモデルを考えて，対応する最適な 成長スケジュール を求めてみましょう．

成長のモデル

栄養体の量を $x$，繁殖体の量を $y$ とします．もし仮に栄養成長のみを続けるとした場合には，次のような微分方程式になります：

\frac{\mathrm{d}x}{\mathrm{d}t}
=rx.

$t$は時間を表す変数です．また，$r$は成長率で，栄養体による光合成の効率を表します（$r$が大きければ大きいほど光合成の効率が良くて成長にまわすことができます）．

ここから繁殖成長も考えると，次のような連立微分方程式を書くことができます：

\left\{\begin{aligned}
\frac{\mathrm{d}x}{\mathrm{d}t}
&=\{1-u(t)\}rx,\\
\frac{\mathrm{d}y}{\mathrm{d}t}
&=u(t)rx.
\end{aligned}\right.

$u$ は繁殖成長に割く光合成産物の割合を表し，$0\le u(t)\le 1$をみたす関数です．$u=1$は繁殖成長のみをすることを表し，$u=0$は栄養成長のみをすることを表します．ここでは一年生植物を考えて，春 $t=0$ に芽吹き $t=T$ に1年が経つとしましょう．

目的は，最終的な繁殖体 $y(t=T)$ を最大化するような関数 $u(t)$（成長スケジュール）を求めることです．
以下ではまず数値計算によって得られる最適な成長スケジュールを紹介します．その後，Pontryagin の最大原理を使って最適化問題を解き，数値計算による結果と一致することを確認します．

最適な成長スケジュール：数値計算

先の連立微分方程式において，$t\to kt$ なる変換をすることは $r\to kr$ なる変換と等価なので，数値計算においては $T=1$ と固定して $r$ をいろいろと変えてみることにします．

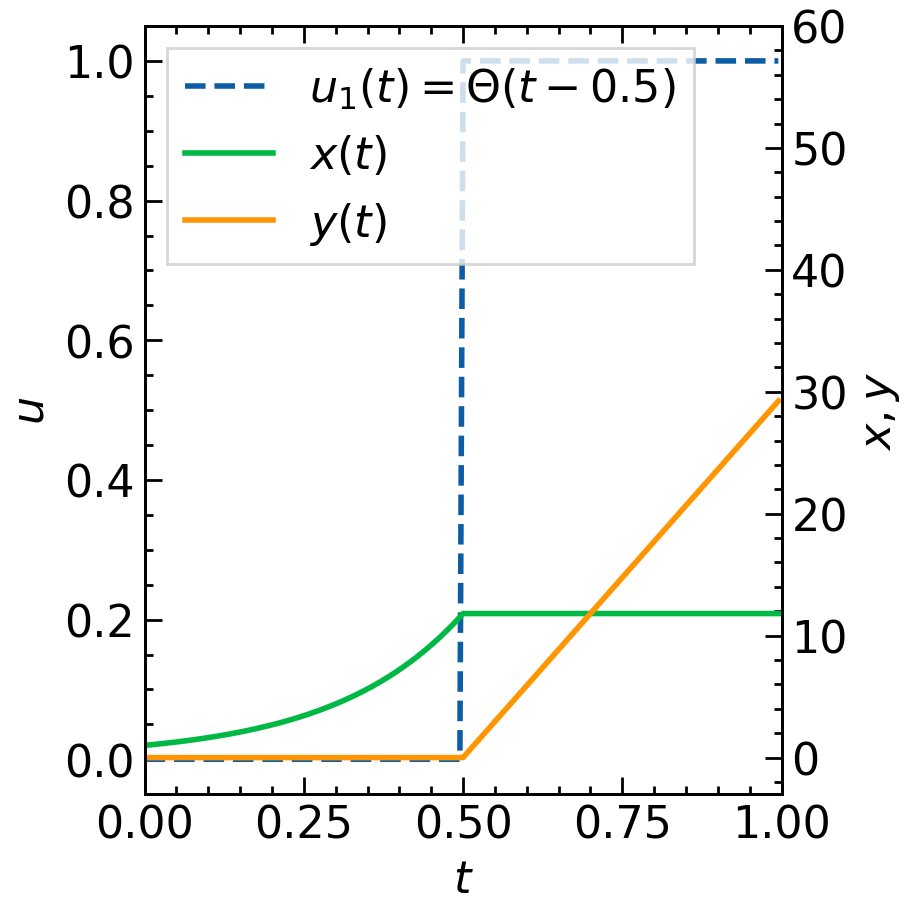
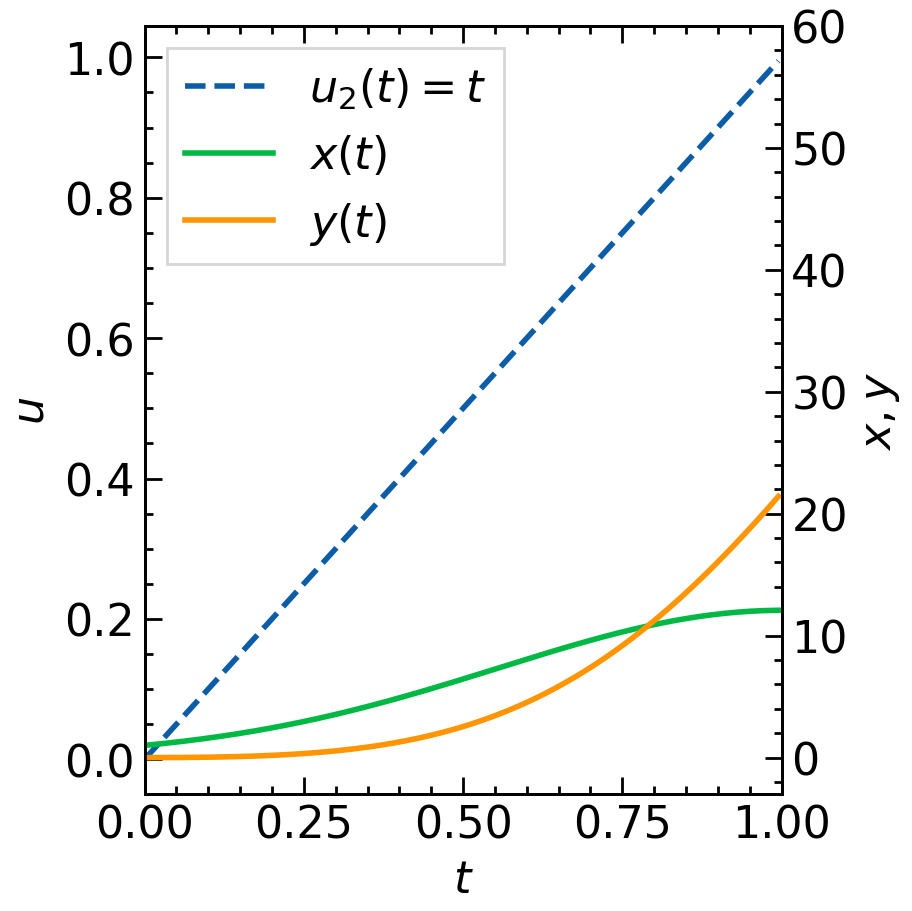
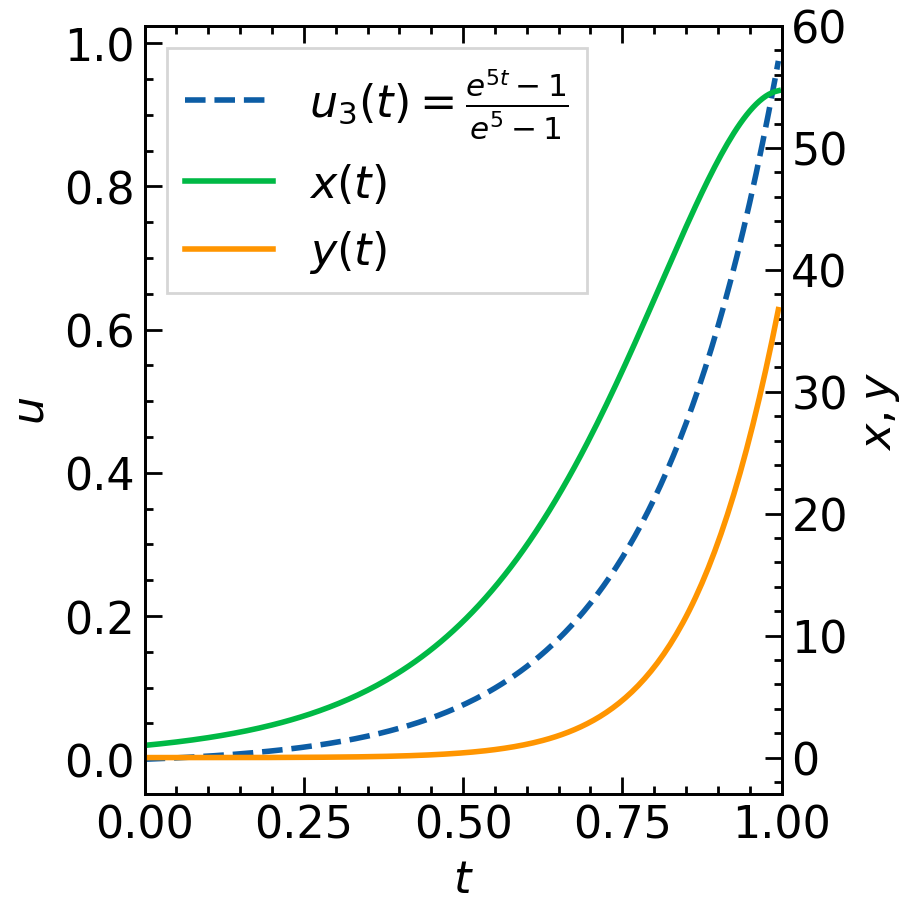
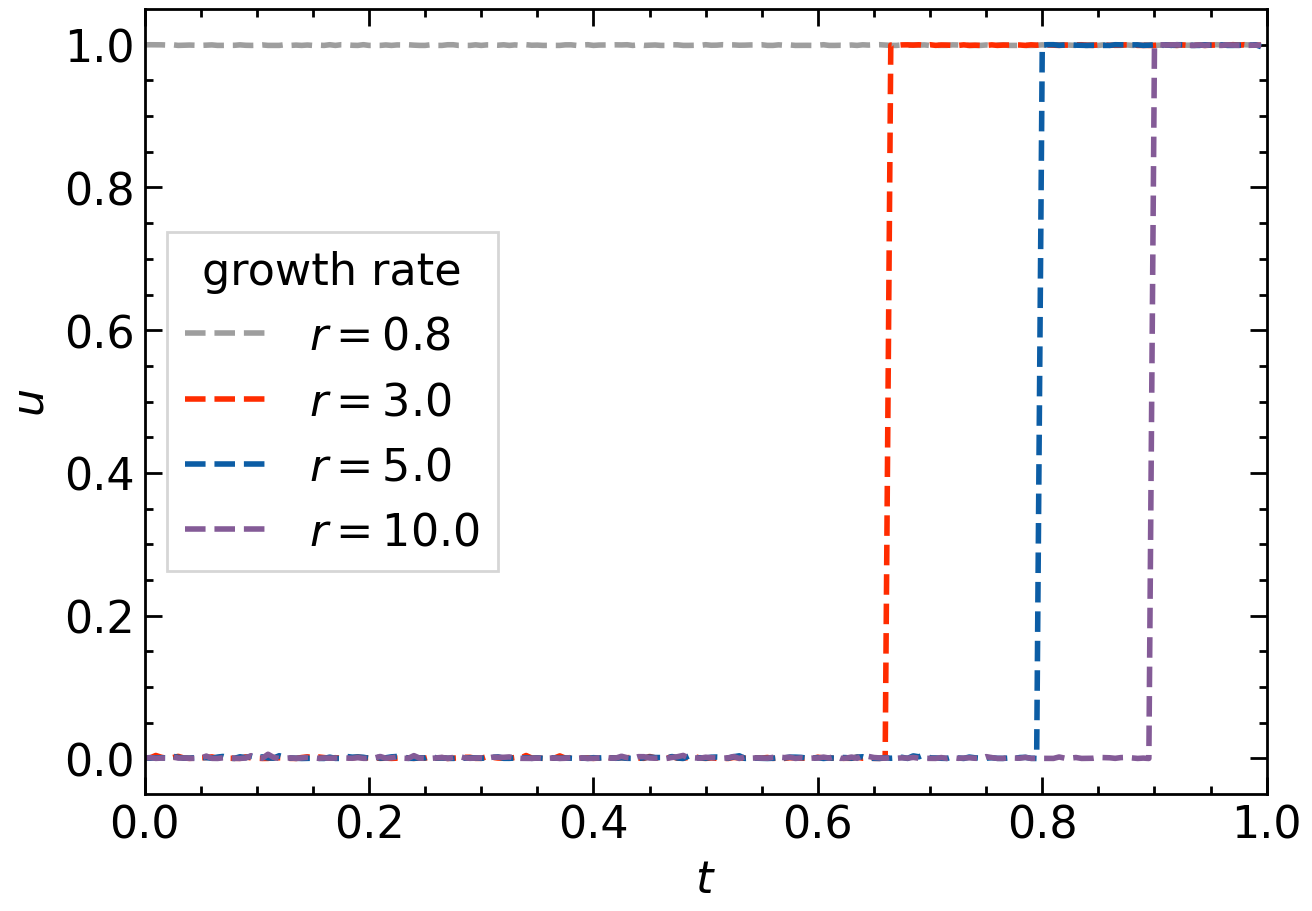
まずは，いろいろな関数 $u(t)$ に対して $x(t),y(t)$ を計算してみましょう．階段関数 $u_1(t)$，1次関数 $u_2(t)$，指数関数 $u_3(t)$ に対して数値計算をしたものを下図に並べました．いずれも $x(0)=1,y(0)=0,r=5$ としています．
注目すべき点は繁殖体 $y$ の最終的な量 $y(T)$ で，オレンジ線の右端の値が対応しています．この $y(T)$ を最大にするような関数 $u(t)$ を求めるのが目的です．

最適化の詳しい数値計算の手法は割愛しますが，$t=T$ から始めて最適な $u$ を探索しながら時間後退させて $u(t)$ を求めています．現実の植物は長い年月をかけて $u(t)$ を更新（進化）し最適化（適応）をしていると言えるでしょう．
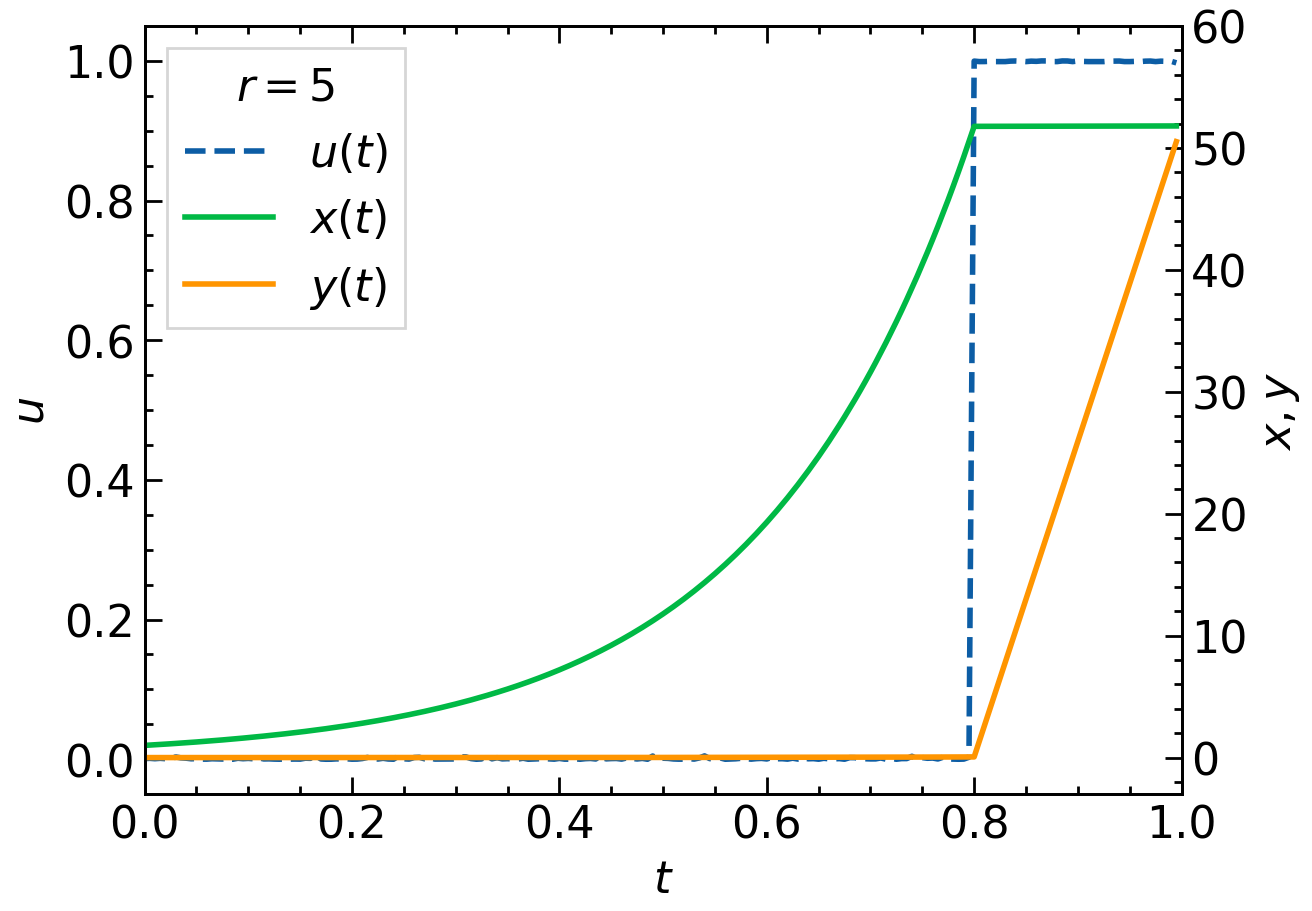
数値計算をしてみると，$u(t)\equiv1$ または階段関数が最適な $u(t)$ になるということがわかります（右下図）．$r$の値を変えると，階段関数の立ち上がり時刻 $t$ が変わっています．
$x(t),y(t)$ にも着目してみましょう．はじめは $u(t)=0$なので，$y(t)=0$ のままで $x(t)$ が指数関数的に増えます．$u(t)=1$ に切り替わると，$x(t)$ の増加が止まり，ここまでで増やすことに成功した $x(t)$ を使って $y(t)$ が線形に増加します．$t=T$ での $x,y$ について $x(T)=y(T)$ が成り立っていることも特徴的です．

少なくとも数値計算によって，繁殖体の最終量 $y(T)$ を最大化する成長スケジュール $u(t)$ は，はじめは $u(t)=0$ で途中から $u(t)=1$ という階段関数になっていることがわかりました．はじめは栄養成長に集中し，栄養体が十分に大きくなってから一気に繁殖成長をするという流れが最適だということです．この「一気に繁殖成長」するタイミングが秋に対応していて，多くの植物が秋になって一気に果実を実らせます．

最適な成長スケジュール：Pontryagin の最大原理

制御変数 $u$ をどのような関数にすれば目的変数を最大化（最小化）できるのかを与えるもので，Pontryagin の最大原理 というものがあります．ここでは Pontryagin の最大原理（の今回の場合に適用できるバージョン）を簡単に紹介し，先ほどの成長モデルに適用します．

Pontryagin の最大原理

区間 $t_0\le t\le t_1$ を考えます． $\boldsymbol{x}=(x^1,\ldots,x^n)$ が次のような微分方程式に従うとします：

\frac{\mathrm{d}x^i}{\mathrm{d}t}
=f^i(\boldsymbol{x},u),\quad
i=1,\ldots,n.

ただし $f^i(\boldsymbol{x},u)$ は $\boldsymbol{x},u$ について連続，$\boldsymbol{x}$ について微分可能であるとします．
$\boldsymbol{x}$ の初期条件を $\boldsymbol{x}(t_0)=\boldsymbol{x}_0$ としておきましょう．目的は次の量 $J[u(t)]$ を $u(t)$ について最大化することです：

J
=\int_{t_0}^{t_1}f^0(\boldsymbol{x}(t),u(t))\,\mathrm{d}t.

ただし閉領域 $U$ に対して $u\in U$ とする．$f^0(\boldsymbol{x},u)$ は $f^i(\boldsymbol{x},u),(i=1,\ldots,n)$ と同様に $\boldsymbol{x},u$ について連続で $\boldsymbol{x}$ について微分可能であるとします．ここで出てきた関数 $f^0(\boldsymbol{x},u)$ を使って新しい変数 $x^0$ を次の微分方程式に従うように導入しておきます：

\frac{\mathrm{d}x^0}{\mathrm{d}t}
=f^0(\boldsymbol{x},u).

$\boldsymbol{x}=(x^1,\ldots,x^n)$ の微分方程式とまとめて書くと，次のように書くことができます：

\frac{\mathrm{d}x^i}{\mathrm{d}t}
=f^i(\boldsymbol{x},u),\quad
i=0,\ldots,n.

ここで，補助変数 $\psi^0,\boldsymbol{\psi}=(\psi^1,\ldots,\psi^n)$ を次の微分方程式に従う変数として導入します：

\frac{\mathrm{d}\psi^i}{\mathrm{d}t}
=-\sum_{j=0}^n\frac{\partial f^j(\boldsymbol{x},u)}{\partial x^i}\psi^j,\quad
i=0,\ldots,n.

上の $\boldsymbol{\Psi}=(\psi^0,\boldsymbol{\psi})$ は，初期条件を与えることで一意に解くことができます．
$\boldsymbol{x}$ と導入した補助変数 $\boldsymbol{\Psi}$ ，および関数 $\boldsymbol{F}(\boldsymbol{x},u)=(f^0(\boldsymbol{x},u),f^1(\boldsymbol{x},u),\ldots,f^n(\boldsymbol{x},u))$ を使ってハミルトニアンを

H(\boldsymbol{\Psi},\boldsymbol{x},u)
=\boldsymbol{\Psi}\cdot\boldsymbol{F}(\boldsymbol{x},u)
=\sum_{j=0}^n\psi^jf^j(\boldsymbol{x},u)

と定義しましょう．このハミルトニアンを使って $\boldsymbol{X}=(x^0,\boldsymbol{x})$ と $\boldsymbol{\Psi}=(\psi^0,\boldsymbol{\psi})$ の従う微分方程式は次のように書き換えることができます：

\left\{\begin{aligned}
\frac{\mathrm{d}x^i}{\mathrm{d}t}
&=\frac{\partial H}{\partial \psi^i},\\
\frac{\mathrm{d}\psi^i}{\mathrm{d}t}
&=-\frac{\partial H}{\partial x^i},
\end{aligned}\right.
\quad
i=0,1,\ldots,n.

このとき，$u(t)$ が最適であるための1つの必要条件は，次の2つの条件をみたす非零なベクトル関数 $\boldsymbol{\Psi}(t)=(\psi^0(t),\psi^1(t),\ldots,\psi^n(t))$ が存在することです．

1. すべての $t\in[t_0,t_1]$ に対して変数 $u\in U$ の関数 $H(\boldsymbol{\Psi}(t),\boldsymbol{x}(t),u)$ が点 $u=u(t)$ において最大値をとる：

   H(\boldsymbol{\Psi}(t),\boldsymbol{x}(t),u(t))
   =\sup_{u(t)\in U}H(\boldsymbol{\Psi}(t),\boldsymbol{x}(t),u(t)).
   

2. $\boldsymbol{\Psi}(t_1)=(1,0,\ldots,0)$．

成長モデルの最適化

Pontryagin の最大原理を使って実際に成長モデルを最適化してみましょう．考えていた成長モデルは次のようなものでした：

\left\{\begin{aligned}
\frac{\mathrm{d}x^2}{\mathrm{d}t}
&=f^1(x^1,x^2,u)=(1-u)rx^1,\\
\frac{\mathrm{d}x^2}{\mathrm{d}t}
&=f^2(x^1,x^2,u)=urx^1.
\end{aligned}\right.

ここで，Pontryagin の最大原理のノーテーションに揃えて $x\to x^1,y\to x^2$ と書き換えています．$x^2(T)$ を最大化したいので，

J
=x^2(T)
=\int_0^T\frac{\mathrm{d}x^2}{\mathrm{d}t}\,\mathrm{d}t
=\int_0^Turx^1\,\mathrm{d}t

となり，$f^0(x^1,x^2,u)=urx^1$ となります（$t_0=0,t_1=T$としました）．このときのハミルトニアンは，

\begin{align}
    H(\psi^0,\psi^1,\psi^2,x^1,x^2,u)
    &=\sum_{j=0}^2\psi^jf^j(x^1,x^2,u)\\
    &=ur\psi^0x^1+(1-u)r\psi^1x^1+ur\psi^2x^1.
\end{align}

$\psi^0,\psi^1,\psi^2$ の従う微分方程式は，

\begin{align}
    \frac{\mathrm{d}\psi^0}{\mathrm{d}t}
    &=-\frac{\partial H}{\partial x^0}
    =0,\\
    \frac{\mathrm{d}\psi^1}{\mathrm{d}t}
    &=-\frac{\partial H}{\partial x^1}
    =-ur\psi^0-(1-u)r\psi^1-ur\psi^2,\\
    \frac{\mathrm{d}\psi^2}{\mathrm{d}t}
    &=-\frac{\partial H}{\partial x^2}
    =0.
\end{align}

Pontryagin の最大原理により，$\boldsymbol{\Psi}(T)=(\psi^0(T),\psi^1(T),\psi^2(T))=(1,0,0)$ なので，$\psi^0(t)\equiv1,\psi^2(t)\equiv0$となります．あらためてハミルトニアンと $\psi^1(t)$ の微分方程式を書き直すと，次のようになります：

\begin{gather}
    H(\psi^1,x^1,x^2,u)
    =urx^1+(1-u)r\psi^1x^1,\\
    \frac{\mathrm{d}\psi^1}{\mathrm{d}t}
    =-ur-(1-u)r\psi^1.
\end{gather}

$\psi^1(t)$ の微分方程式を一般の $u(t)$ に対して解きましょう．微分方程式は次のように書き換えることができます：

\frac{\mathrm{d}\psi^1}{\mathrm{d}t}
=-(1-u)r(\psi^1-1)-r.

これを定数変化法で解きましょう．$r=0$ としたときは，

\begin{align}
    \frac{\mathrm{d}\widetilde{\psi}^1}{\mathrm{d}t}
    &=-(1-u)r(\widetilde{\psi}^1-1)\\
    \therefore\quad
    \widetilde{\psi}^1(t)
    &=A\exp\left[-r\int_0^t\mathrm{d}t'\,(1-u(t'))\right]+1.
\end{align}

もとの微分方程式（$r\ne0$）の解を

\psi^1(t)
=A(t)\exp\left[-r\int_0^t\mathrm{d}t'\,(1-u(t'))\right]+1

の形でおきます．微分方程式に代入すると，

\frac{\mathrm{d}A}{\mathrm{d}t}
=-r\exp\left[r\int_0^t\mathrm{d}t'\,(1-u(t'))\right]

となり，これを解いて

A(t)
=-r\int_0^t\mathrm{d}t'\,\exp\left[r\int_0^{t'}\mathrm{d}t''\,(1-u(t''))\right]+A_0.

したがって $\psi^1(t)$ は，

\begin{gather}
    \psi^1(t)
    =A(t)\exp\left[-r\int_0^t\mathrm{d}t'\,(1-u(t'))\right]+1,\\
    A(t)
    =-r\int_0^t\mathrm{d}t'\,\exp\left[r\int_0^{t'}\mathrm{d}t''\,(1-u(t''))\right]+A_0.
\end{gather}

まず $u(0)$ を求めます．$t=0$ において$\psi^1$ は $\psi^1(0)=A_0+1$ となります．これはもはや $u$ には依らず，ハミルトニアンは

\begin{align}
    H
    &=urx^1+(1-u)r\psi^1x^1\\
    &=-ur(\psi^1-1)x^1+r\psi^1x^1
\end{align}

となるので，$H$ を最大にする $u$ は，

u(0)
=\left\{\begin{align}
&0&(A_0>0),\\
&1&(A_0<0).
\end{align}\right.

1. $A_0<0$ のとき．先の結果から $u(0)=1$ です．$t=\tau$ まで $u(t)=1$ であるのが最適であるとする（$\tau=0$ でも良い）と，$0\le t\le\tau$ において $\psi^1(t)=-rt+A_0+1$ となり，ハミルトニアンは $H=-ur(-rt+A_0)+r\psi^1x^1$ です．$A_0<0$ なので $t\ge0$ で $-rt+A_0<0$ となり，最後まで $u(t)\equiv1$ であるのが最適ということになります．境界条件 $\psi^1(T)=0$ より $-rT+A_0+1=0$ となり，$A_0<0$ から $rT<1$ が必要になります．

2. $A_0>0$ のとき．はじめは $u(0)=0$ が最適です．$t=\tau$ までは $u(t)=0$ が最適であるとすると，$0\le t\le \tau$ における $\psi^1(t)$ は，先ほど求めた一般解を使うことで（もしくは微分方程式を解くことで）

   \psi^1(t)
   =(A_0+1)e^{-rt}\quad
   (0\le t\le \tau)
   

   となります．このときのハミルトニアンは，

   H
   =-ur\left[(A_0+1)e^{-rt}-1\right]+r(A_0+1)e^{-rt}x^1\quad
   (0\le t\le \tau).
   

   $u$ の係数をみればわかるように，$(A_0+1)e^{-rt}-1>0$ であれば $u(t)=0$ が最適で，$(A_0+1)e^{-rt}-1=0$ なる $t(=\tau)$ を境に $u(t)=1$ が最適となります．$\tau<t\le T$ では

   \psi^1(t)=-r(t-\tau)+1\quad
   (\tau<t\le T)
   

   となり，このときのハミルトニアンは，

   H
   =ur^2(t-\tau)x^1+r\{-r(t-\tau)+1\}x^1\quad
   (\tau<t\le T).
   

   したがって $\tau<t\le T$ では $u(t)=1$ が最適です．境界条件 $\psi^1(T)=0$ より $-r(T-\tau)+1=0$ となり，$\tau$ が

   \tau
   =T-\frac{1}{r}
   

   と求められます．$\tau\ge0$ から $rT\ge1$ が必要であるとわかります．

以上の結果をまとめると，最適な $u(t)$ は次のようになります：

u(t)
=\left\{\begin{aligned} 
&1&(rT<1),\\
&\Theta(t-\tau)&(rT\ge1),
\end{aligned}\right.
\quad
\tau=T-\frac{1}{r}.

また，$rT\ge1$ の場合に $x(T),y(T)$ を計算すると，$x(T)=y(T)=x_0e^{-r\tau}$ となって一致します．

実際はどうか

単純な成長モデルを考えると，はじめは葉・茎・根を伸ばし，ある程度成長してから一気に実・種子をつけるのが最も良いという結論に至るのですが，これは実際の植物のいくつかの事象を説明できているようです（以下は講義「進化生態学」の受け売り）：

• 栄養不足などによって成長率 $r$ が小さくなると，本来は秋に花芽分化する植物が夏に花芽分化することがあるようです．これは $\tau=T-1/r$ で $r$ が小さくなると $\tau$ が短くなるということに対応しています．実際に花芽分化促進用のハイポネックスには窒素が含まれていないようです．
• 一年生植物は暗期が長くなることで秋を察し，花芽分化を促進します．$\tau=T-1/r$ の $T$ がわからなければ最適な $\tau$ を知ることができないので，$T$ を知る仕組みが備わっているように思います．
• イネなどで栄養体と穂の重量比がおよそ $1:1$ になることが知られています．$x(T)=y(T)$ に対応していそうです．
• 果樹の場合「桃栗三年柿八年」で知られるように，はじめのうちは実をつけずに根や幹・枝を伸ばすことに集中します．落葉樹だと年単位で葉を落としリセットするので，根・幹・枝が $y$ に対応し，秋にはこれらを最大化するように成長を分配しているようです．

今回は秋に実をつける一年草のお話でしたが，当然それぞれの季節で「旬」となる食べ物がたくさんあります．みなさんも時には植物の進化を考えながら「旬」を楽しんでみてはいかがでしょうか？

参考文献

• Pontryagin, Lev Semenovich. Mathematical theory of optimal processes. CRC press, 1987.