はじめに
こんにちは,こんばんは,いぇとです.
この記事は東京大学理学部物理学科 B3 有志による Physics Lab. 2022 Advent Calendar 2021 12日目の記事です.
Physics Lab. とは物理学科有志による五月祭企画で,普段はゼミをやったり春休みには実験をしたりして,五月祭で何かしらを展示する予定です.その中で私は生物物理班に所属しています.生物物理おもしれ〜.生物物理班については,たがやし班長が書いてくれた記事「生物物理班だよ」を見てね.
何の記事を書こうか迷っていたのですが,生物物理のことを書くと五月祭で出すネタと衝突しそうですし,ふざけたものを書きたかったので,生物物理については書きません.今回は普段私が愛用している TikZ について簡単な紹介をしようと思います.
先に言っておくと,私はほとんど脚注を付けずにカッコなどを使おうと思います.(PDF などであればいいのですが)どうも Web 上の脚注は行ったり来たりしないといけないのが苦手なんですよね.
またこの記事は LaTeX の基本事項を前提としています.
やること
何かを描くことをこの記事の目標とします.何か描くものないかな〜と Twitter に投げたところ,次のようなものを投げられました.
- Barnsley fern(採用)
- イーブイ(かわいい)
- トーラス(立体いやだ)
- 正十二面体(立体いやだ)
- 東大の校章(アリ)
- 哀ちゃん(「バカね」)
- こけし(採用)
- 吉岡書店の表紙のやつ(アリ)
トーラスや正十二面体は描こうと思えばできますが,(自分の実力では)複雑な立体をきれいに表示できないので不採用.イーブイや哀ちゃんは画力がないので不採用(気が向いたら作る).東大の校章や吉岡書店の表紙はアリですが,少し面倒なので不採用.
ということで, Barnsley fern とこけしが採用されました.当選者の方おめでとうございます.
追加で,私が過去にレポートで描いたものとしてトポロジカル欠陥を載せておきます.
TikZ とは
TikZ は TeX 用の描画パッケージです.正確には PGF が描画パッケージで,TikZ は PGF のフロントエンドの一つというだけですが,私の記事の範囲では TikZ を用いて図を描くことを取り上げるので,そこまで気にしなくて良いです.また,私は TikZ をティクスと発音しています.伝わればなんでも良いです.
今回は TikZ の細かな文法を一つ一つ扱うことはしません.本当は一から説明したい気持ちがありますが,長くなると読むのも疲れるはずなのでやめておきます.(TikZ の基本文法について個人的に記事を上げようともしましたが,めんどくさくて全然書いていません.身内は私に直接聞いてくれれば知っている範囲で答えます.)
TikZ の基本的なあれこれ
パッケージの読み込み
早速中身に入ります.まずは TikZ パッケージを読み込みます.
\usepackage{tikz}
PGF は TikZ と一緒に自動的に読み込まれるっぽいですね.color パッケージあたりも自動的に読み込まれてそうです.詳しくないので何かエラーを吐いたら適当なパッケージを追加で読み込んでください.
tikzpicture 環境
TikZ は基本的に tikzpicture 環境を使います.
\begin{tikzpicture}[option]
\end{tikzpicture}
必要に応じて option を付けてください.私は scale をいじることが多いです.
\draw, \fill, \filldraw
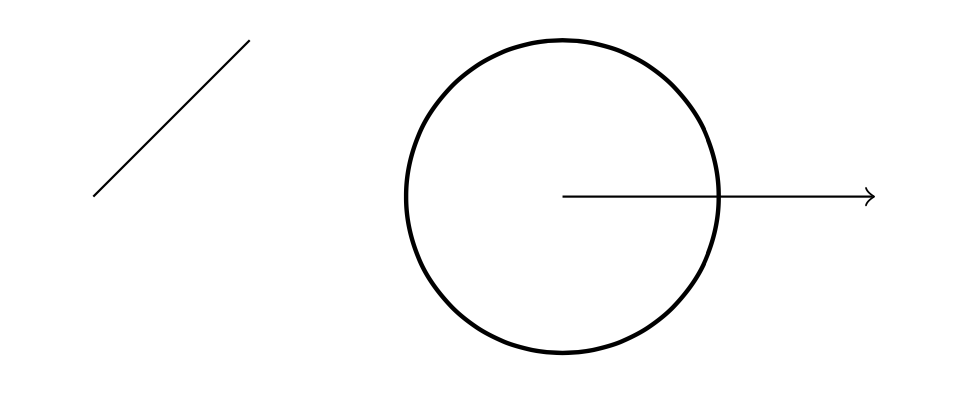
図を描く上でもっとも基本的なコマンドは \draw です.線が描けます.たとえば次のような具合です.
\begin{tikzpicture}
\draw (0,0) -- (1,1); %(0,0)から(1,1)への線分
\draw[thick] (3,0) circle(1); %中心座標(3,0)半径1の円で線が1段階太い
\draw[->] (3,0) -- (4,0); %(3,0)から(4,0)への矢印
\end{tikzpicture}
; の付け忘れに注意してください.
塗りつぶしは \fill を使います.\draw と \fill を組み合わせた \filldraw もあります.
\begin{tikzpicture}
\fill[pink] (0,0) -- (1,1) -- (0,1) -- cycle; %cycleで始点に戻りpinkで塗りつぶし
\filldraw[fill=orange] (4,0) circle(2 and 1); %半径が2と1の楕円をorangeで塗りつぶし
\end{tikzpicture}
TikZ の処理は上の行から順に行われます.そのことを念頭におくと,図形の重なりの処理も自然と理解できます.
\begin{tikzpicture}
\filldraw[orange] (1,0) circle(1);
\filldraw[cyan] (2,0) circle(1);
\end{tikzpicture}
PGF の便利なものたち
TikZ に限らず使える便利なものたちを紹介します.これを知っていると最強になれる気がします.
\foreach
\foreach は繰り返し処理をしてくれます.
\foreach \i in {1,2,...,10}{\i, }
出力:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
\pgfmathsetmacro
\pgfmathsetmacro は変数を作ったり書き換えたりすることができます.
\pgfmathsetmacro{\a}{1}
\pgfmathsetmacro{\b}{exp(\a)}
\pgfmathsetmacro{\c}{sqrt(2)}
\pgfmathsetmacro{\d}{\c^2}
a=\a, b=\b, c=\c, d=\d
出力:
a=1, b=2.71825, c=1.41421, d=2.0
PGF に計算処理を投げる際には注意が必要です.たとえば次の例をみましょう.
\pgfmathsetmacro{\x}{-2}
\pgfmathsetmacro{\a}{\x^2}
\pgfmathsetmacro{\b}{(\x)^2}
x=\x, a=\a, b=\b
出力:
x=-2.0, a=-4.0, b=4.0
a と b で計算結果が違います.これは PGF の処理として,文字列のまま代入して計算処理をしているために -2^2 と (-2)^2 で計算結果が異なっています.結構罠なので気を付けましょう.(私もはじめのうちは x^2 のプロットをして奇関数が出てきた!と悩んだ時期がありました.)
\pgfmathparse, \pgfmathresult
\pgfmathparse は何かしらの解析の処理をしてくれて,\pgfmathresult は直近の \pgfmathparse の結果を返してくれます.
\pgfmathsetmacro{\x}{1}
\pgfmathsetmacro{\y}{-1}
\pgfmathparse{\x>0}
\verb|x>0|: \pgfmathresult,
\pgfmathparse{not(or(\x>0,\y>0))}
\verb|not(or(x>0,y>0))|: \pgfmathresult,
\pgfmathparse{(\x)*(\y)}
\verb|x*y|: \pgfmathresult
出力:
x>0: 1, not(or(x>0,y>0)): 0, x*y: -1.0
これらの処理は \pgfmathsetmacro でもできるので,そちらを使う方が便利かもしれません.
random
PGF は乱数生成もできます.線形合同法による擬似乱数が生成されているみたいです.今回用いる random(n,m) は n から m まで(両端含む)の整数乱数を生成してくれます.
\foreach \i in {1,2,...,10}{
\pgfmathsetmacro{\n}{random(0,9)}
\n,
}
出力:
7, 0, 7, 8, 3, 4, 9, 7, 5, 6,
\ifnum, \else, \fi
\ifnum は if 文を書けます.\ifnum の直後に条件式を,\else で条件式が偽の場合の処理,\fi で if 文を閉じます.
\foreach \i in {1,2,...,6}{
\pgfmathparse{int(mod(\i,2))}
\ifnum \pgfmathresult=1
odd,
\else
even,
\fi}
出力:
odd, even, odd, even, odd, even,
こけし
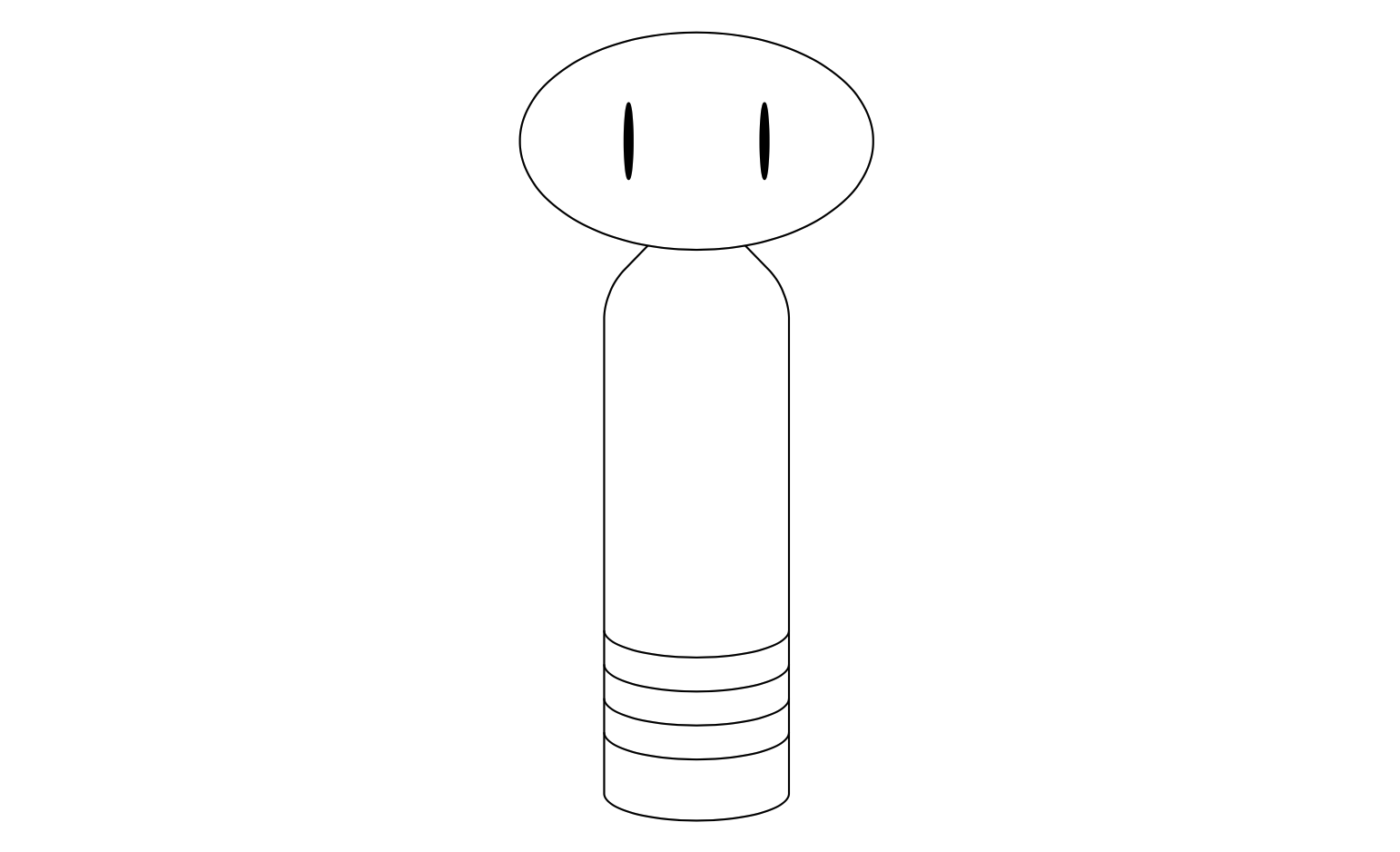
あらゐけいいち氏作のこけしを描きます.まずはべたがき.
使っているコマンドについて少し説明します.
-
circleは円を描くコマンドです.circle(r)で半径 r の円が描けます. -
circle(r1 and r2)とすると x, y 方向の半径がそれぞれ r1, r2 の楕円になります. -
arcは円弧を描くコマンドです.arc(a:b:r)で a, b をそれぞれ始端と終端の角度として半径 r の円弧を描きます.rの部分をr1 and r2として楕円弧にできます. -
rounded cornersで角を丸くします.sharp cornersで丸くなった角を戻します.
\begin{tikzpicture}
%持ちやすそうなところ
\draw[rounded corners=2mm] (0,-0.4)
-- (-0.68,-1.1)[sharp corners]
-- (-0.68,-4.8) arc(-180:0:0.68 and 0.2)
[rounded corners=2mm] -- (0.68,-1.1)
-- (0,-0.4);
%3本帯
\draw (-0.68,-4.35) arc(-180:0:0.68 and 0.2);
\draw (-0.68,-4.10) arc(-180:0:0.68 and 0.2);
\draw (-0.68,-3.85) arc(-180:0:0.68 and 0.2);
\draw (-0.68,-3.60) arc(-180:0:0.68 and 0.2);
%頭
\filldraw[fill=white] (0,0) circle(1.3 and 0.8);
%目
\filldraw (-0.5,0) circle(0.03 and 0.28);
\filldraw (0.5,0) circle(0.03 and 0.28);
\end{tikzpicture}
ほとんど良さそうです.先ほど繰り返し処理などを説明したので,それらを使って書き換えてみます.
具体的には,3本帯の部分を \foreach で繰り返し処理に書き換えます.また繰り返し出てくる胴体の半径を \r としておきます.こうすると \r の値を弄るだけでこけしの胴体の太さを全体にわたって調整できます.
\begin{tikzpicture}
\pgfmathsetmacro{\r}{0.68} %こけしの胴体断面の半径
%持ちやすそうなところ
\draw[rounded corners=2mm] (0,-0.4)
-- (-\r,-1.1)[sharp corners]
-- (-\r,-4.8) arc(-180:0:{\r} and 0.2)
[rounded corners=2mm] -- (\r,-1.1)
-- (0,-0.4);
%3本帯
\foreach \i in {0,1,2,3} \draw (-\r,{-4.35+0.25*\i}) arc(-180:0:{\r} and 0.2);
%頭
\filldraw[fill=white] (0,0) circle(1.3 and 0.8);
%目
\filldraw (-0.5,0) circle(0.03 and 0.28);
\filldraw (0.5,0) circle(0.03 and 0.28);
\end{tikzpicture}
最後に色塗りと細かい調整をしておきます.おっと,色の話はいままであまりしてこなかったですね.
-
\definecolorを使うといろんな形式(たとえば RGB)で色を定義できます. -
\colorletを使って色を定義すると,色を薄めたり混ぜたりするのが容易です.たとえば\colorlet{C}{red!50}とすると,redを 50% に薄めたCという色を定義したことになります.
これらのコマンドは実は xcolor パッケージによるもので,文字色の定義などにも使えます.
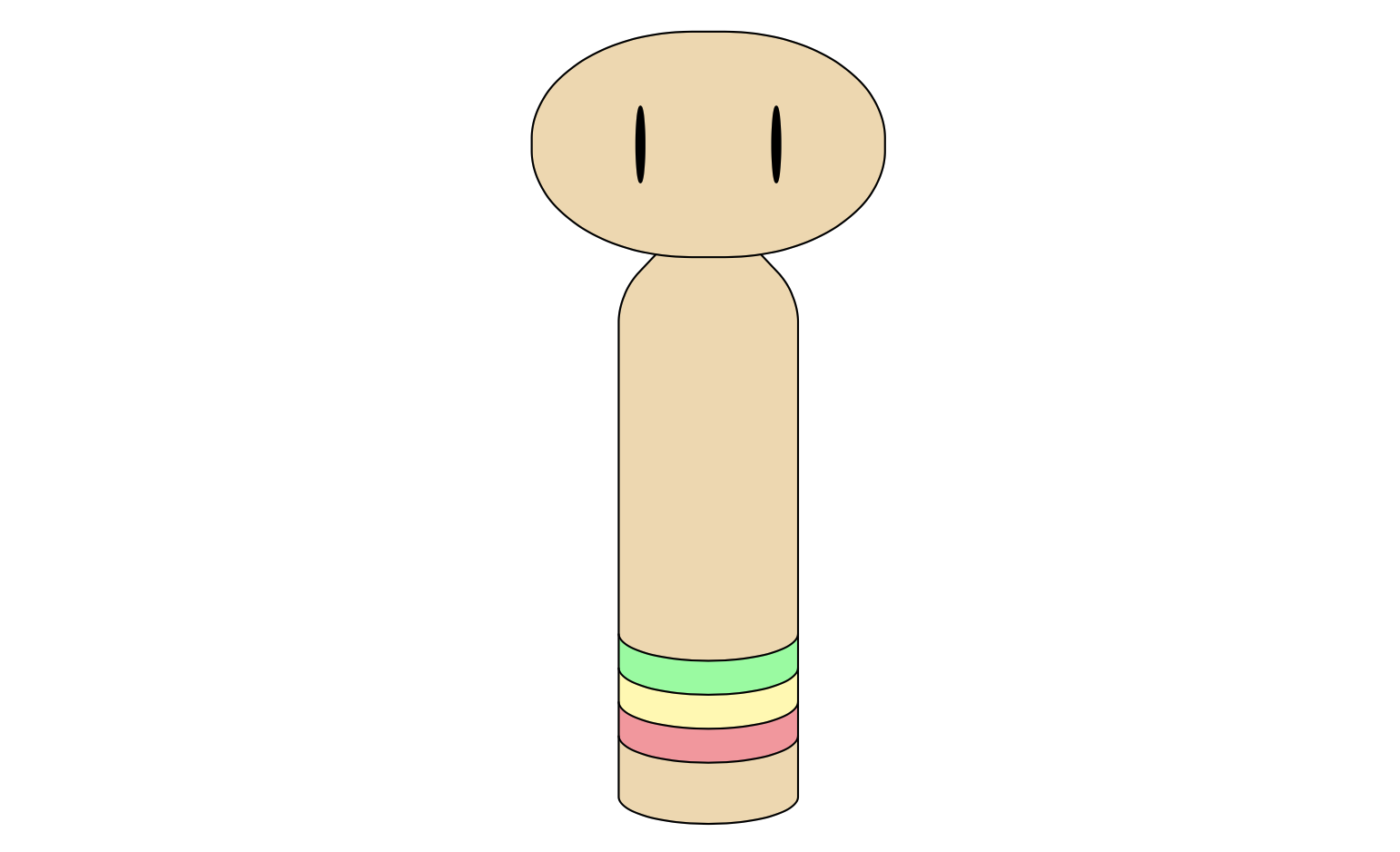
さて,色を塗って細かな調整を入れましょう.
\definecolor{C0}{HTML}{f0dcb4}
\colorlet{C1}{red!35}
\colorlet{C2}{yellow!35}
\colorlet{C3}{green!35}
\begin{tikzpicture}
\pgfmathsetmacro{\r}{0.66} %胴体の太さ
%色塗り
\fill[rounded corners=2mm, fill=C0]
(0,-0.4)
-- (-\r,-1.1)[sharp corners]
-- (-\r,-4.8) arc(-180:0:{\r} and 0.2)
[rounded corners=2mm] -- (\r,-1.1)
-- (0,-0.4);
\foreach \i in {1,2,3}
\fill[C\i] (-\r,{-4.35+0.25*(\i-1)}) arc(-180:0:{\r} and 0.2)
-- (\r,{-4.35+0.25*\i}) arc(0:-180:{\r} and 0.2)
-- cycle;
%持ちやすそうなところ
\draw[rounded corners=2mm] (0,-0.4)
-- (-\r,-1.1)[sharp corners]
-- (-\r,-4.8) arc(-180:0:{\r} and 0.2)
[rounded corners=2mm] -- (\r,-1.1)
-- (0,-0.4);
%3本帯
\foreach \i in {0,1,2,3}
\draw (-\r,{-4.35+0.25*\i}) arc(-180:0:{\r} and 0.2);
%頭
\pgfmathsetmacro{\a}{1.3}
\pgfmathsetmacro{\b}{0.83}
\pgfmathsetmacro{\c}{0.12}
\pgfmathsetmacro{\d}{0.04}
\filldraw[fill=C0] (\c,-\b) arc(-90:0:{\a-\c} and {\b-\d})
-- (\a,\d) arc(0:90:{\a-\c} and {\b-\d})
-- (-\c,\b) arc(90:180:{\a-\c} and {\b-\d})
-- (-\a,-\d) arc(180:270:{\a-\c} and {\b-\d})
-- cycle;
%目
\filldraw (-0.5,0) circle(0.03 and 0.28);
\filldraw (0.5,0) circle(0.03 and 0.28);
\end{tikzpicture}
かわいいね.
Barnsley fern
fern はシダという意味で,シダのフラクタル構造を点の集合として描きます.Barnsley fern そのものについてはあまり触れずに,今回は描くことを目的とします.
Barnsley fern は4種類のアフィン写像 $f_i(\boldsymbol{x})=A_i\boldsymbol{x}+\boldsymbol{v}_i$ によって生成されます.
\begin{bmatrix}
x_{n+1}\\
y_{n+1}
\end{bmatrix}
=\begin{bmatrix}
a_i &b_i\\
c_i &d_i
\end{bmatrix}
\begin{bmatrix}
x_{n}\\
y_{n}
\end{bmatrix}
+\begin{bmatrix}
v_i\\
u_i
\end{bmatrix}
4種類のアフィン写像それぞれのパラメータは次の通りです.パラメータ $p_i$ は確率で,写像 $f_i$ が確率 $p_i$ で選ばれることを意味しています.
| $f_i$ | $a_i$ | $b_i$ | $c_i$ | $d_i$ | $v_i$ | $u_i$ | $p_i$ | 生成部分 |
|---|---|---|---|---|---|---|---|---|
| $f_1$ | $0$ | $0$ | $0$ | $0.16$ | $0$ | $0$ | $0.01$ | 茎 |
| $f_2$ | $0.85$ | $0.04$ | $-0.04$ | $0.85$ | $0$ | $1.60$ | $0.85$ | 連続する小さい葉 |
| $f_3$ | $0.20$ | $-0.26$ | $0.23$ | $0.22$ | $0$ | $1.60$ | $0.07$ | 左側の大きな葉 |
| $f_3$ | $-0.15$ | $0.28$ | $0.26$ | $0.24$ | $0$ | $0.44$ | $0.07$ | 右側の大きな葉 |
早速実装しましょう.TikZ を用いた描画自体は点を打つだけなのでとても簡単です.
\begin{tikzpicture}
\pgfmathsetmacro{\N}{7000} %点の数
\pgfmathsetmacro{\x}{0} %xの初期値
\pgfmathsetmacro{\y}{0} %yの初期値
\foreach \n[remember=\x, remember=\y] in {1,...,\N}{ %前の処理のx,yを保持
\pgfmathsetmacro{\judge}{random(1,100)} %1~100の整数乱数
\ifnum \judge=1 %f1
\pgfmathsetmacro{\X}{0}
\pgfmathsetmacro{\Y}{0.16*\y}
\fi
\pgfmathparse{and(\judge>1, \judge<87)}
\ifnum \pgfmathresult=1 %f2
\pgfmathsetmacro{\X}{0.85*\x+0.04*\y}
\pgfmathsetmacro{\Y}{-0.04*\x+0.85*\y+1.6}
\fi
\pgfmathparse{and(\judge>86, \judge<94)}
\ifnum \pgfmathresult=1 %f3
\pgfmathsetmacro{\X}{0.20*\x-0.26*\y}
\pgfmathsetmacro{\Y}{0.23*\x+0.22*\y+1.6}
\fi
\pgfmathparse{\judge>93}
\ifnum \pgfmathresult=1 %f4
\pgfmathsetmacro{\X}{-0.15*\x+0.28*\y}
\pgfmathsetmacro{\Y}{0.26*\x+0.24*\y+0.44}
\fi
\filldraw (\X,\Y) circle(0.005); %(X,Y)に半径0.005の点
\pgfmathsetmacro{\x}{\X}
\pgfmathsetmacro{\y}{\Y}
}
\end{tikzpicture}
かわいいね.
トポロジカル欠陥
最後に,過去に自分がレポートで描いた2次元平面における液晶分子のトポロジカル欠陥欠陥の模式図を載せておきます.
トポロジカル欠陥の詳しい説明は省略しますが,簡単な説明だけしておこうと思います.
液晶分子は細長く空間反転対称な分子です.液晶分子間には,ネマティック相互作用という「周りと方向を揃えようとする」相互作用があります.したがって,とてもエネルギーが安定なのは全体が全く同じ方向を向いているときです.
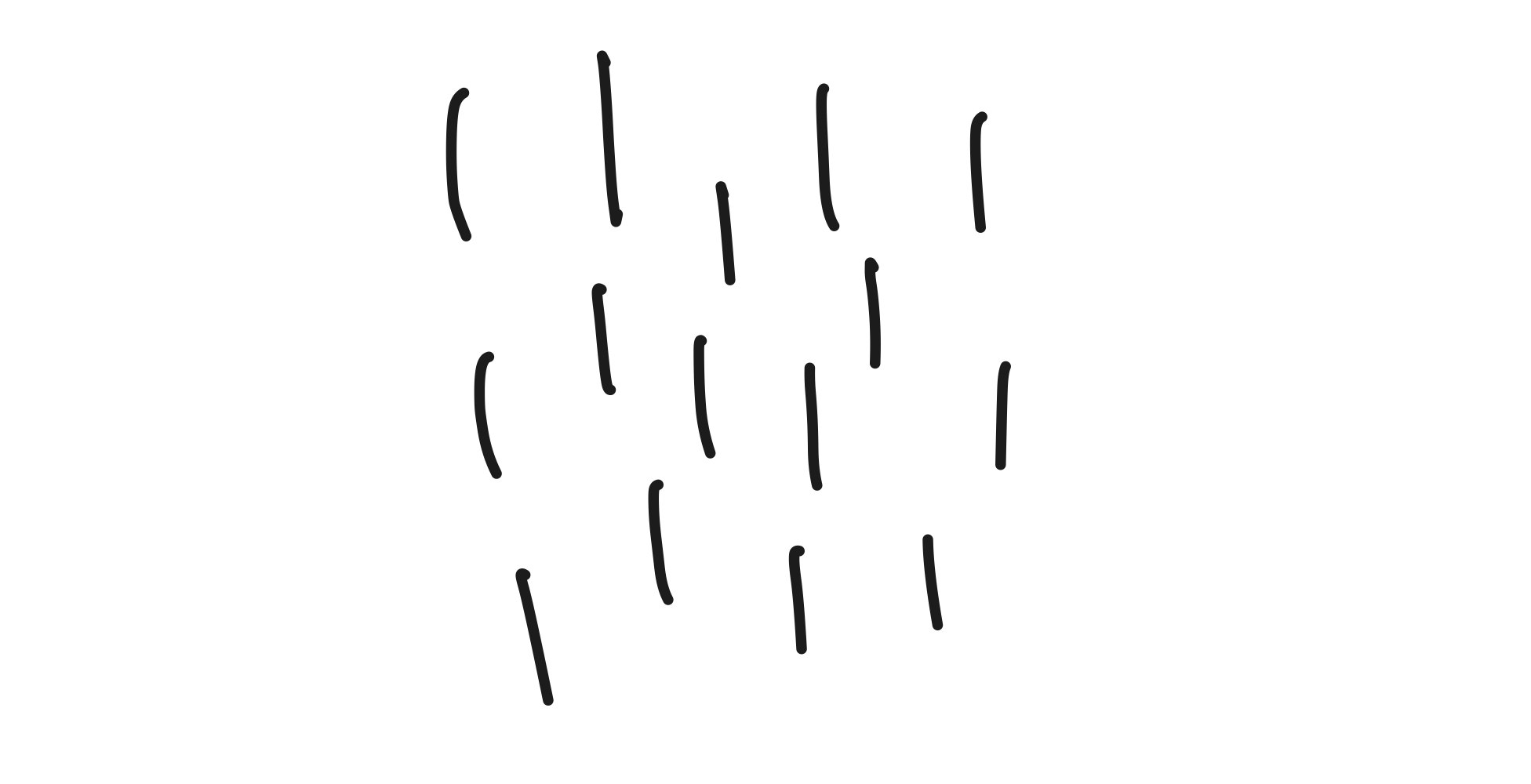
TikZ で図を載せるとネタバレになるので手書きの図を載せました.赤ちゃんが描いたみたいな図だ.
すべて同じ方向を向いていれば安定だから全て同じ方向を向けばええやん!と思うかもしれませんが,実際にはそうもいきません.とても乱雑な状態から始めてネマティック相互作用を与えてやると,次のようなパターンがいくつも生じます.
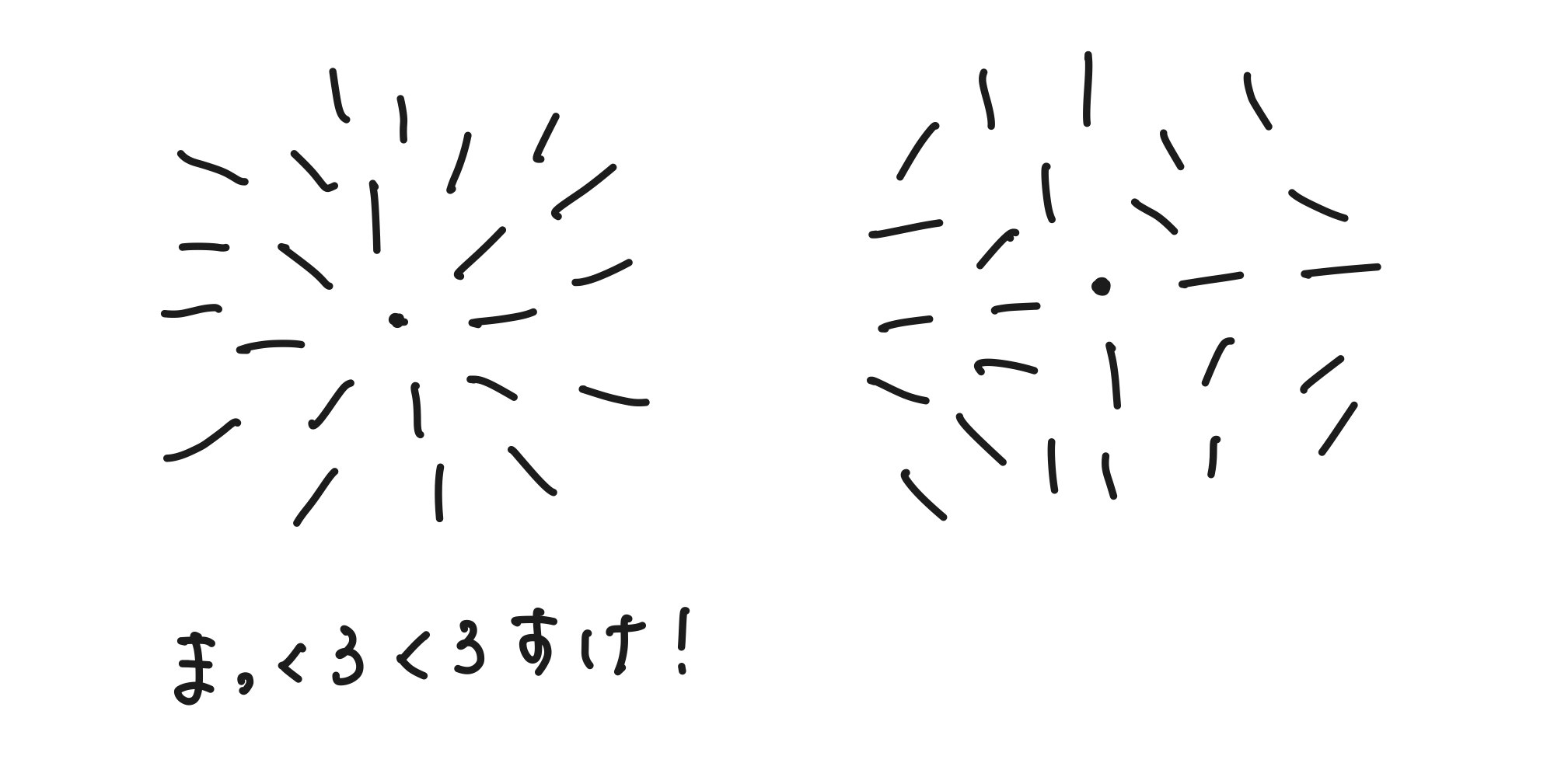
このようなパターンは簡単には消えてくれません.これをトポロジカル欠陥と呼びます.
もう少し準備をしておきましょう.いま,場の(ほとんど)連続な関数として分子の方向を表す角度 $\theta(\boldsymbol{r})$ を考えます.
また,適当な閉曲線 $\Gamma$ をとってきて,その閉曲線に沿って $\theta$ の変化量を線積分します:
$$
\oint_\Gamma\mathrm{d}{\theta}
=\oint_\Gamma\frac{\mathrm{d}\theta}{\mathrm{d}l}\mathrm{d}l
=2k\pi,\quad
k=0,\pm\frac{1}{2},\pm1,\pm\frac{3}{2},\pm2,\ldots.
$$
式に書いた通り,この周回積分の結果は $2\pi$ の半整数倍になります.一周戻ってくると方向が元に戻るためです.液晶分子は空間反転対称で $\theta, \theta+\pi$ が等価なものであることに注意してください.(向きが元に戻る場合は整数倍,方向が元に戻る場合は半整数倍になります.)
この $k$ のことをトポロジカル荷(topological charge)または巻き数といいます.$k\neq0$ の局所点がトポロジカル欠陥です.
ここまで下準備ができたので,いろんな巻き数 $k$ に対するトポロジカル欠陥を TikZ で表示してみましょう.もっとも簡単な場合として,$\theta$ が原点(トポロジカル欠陥の中心)からの方位角 $\phi$ の関数で
$$
\theta=k\phi+c
$$
と書けるときを考えます.これを周回積分すると $2\pi k$ が出てくることは各自で確かめてみてください.
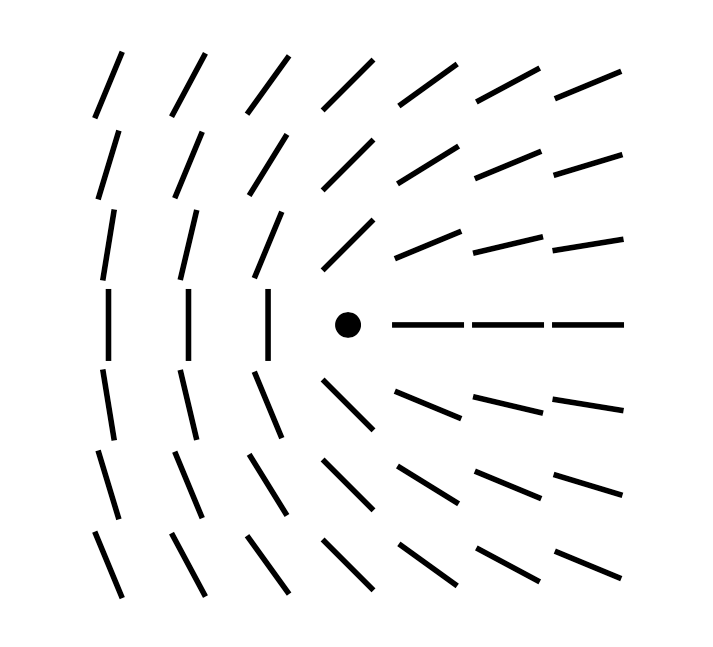
方位角を tan の逆関数 atan で出して,\foreach で液晶分子をたくさん描きます.
%k=-1/2,c=0の場合
\begin{tikzpicture}[scale=0.3]
\pgfmathsetmacro{\k}{-1/2} %巻き数k=-1/2
\pgfmathsetmacro{\c}{0} %c=0
\filldraw (0,0) circle(0.3); %欠陥の中心
\foreach \x in {-6,-4,-2,0,2,4,6} %x=-6,-4,-2,0,2,4,6
\foreach \y in {-6,-4,-2,0,2,4,6}{ %y=-6,-4,-2,0,2,4,6
\pgfmathparse{not(equal(\x,0))}
\ifnum\pgfmathresult=1 %x!=0(atan(inf)を避ける)
\pgfmathparse{\x>0}
\ifnum\pgfmathresult=1 %x>0
\pgfmathsetmacro{\p}{atan(\y/\x)} %phi=atan(y/x)
\else %x<0
\pgfmathsetmacro{\p}{atan(\y/\x)+180} %phi=atan(y/x)+180
\fi
\pgfmathsetmacro{\t}{\k*\p+\c} %theta=k*phi+c
\draw[very thick] (\x,\y) +(\t:-0.9) -- +(\t:0.9); %描画
\else %x=0
\pgfmathparse{not(equal(\y,0))}
\ifnum\pgfmathresult=1 %x=0, y!=0(原点を避ける)
\pgfmathparse{\y>0}
\ifnum\pgfmathresult=1 %x=0,y>0
\pgfmathsetmacro{\p}{90} %phi=90
\else %x=0,y<0
\pgfmathsetmacro{\p}{270} %phi=270
\fi
\pgfmathsetmacro{\t}{\k*\p+\c} %theta=k*phi+c
\draw[very thick] (\x,\y) +(\t:-0.9) -- +(\t:0.9); %描画
\fi
\fi}
\end{tikzpicture}
やった〜.
あとはこれをたくさん描けばいいです.
何回も同じものを描くのは面倒なので \def で \defect を定義してしまいましょう.
中身は先ほどのものとほとんど同じです.
\def\defect#1#2{
\pgfmathsetmacro{\k}{#1}
\pgfmathsetmacro{\c}{#2}
\draw (0,-8.3)node{$k=#1,c=#2$}; %ラベル
\filldraw (0,0) circle(0.3);
\foreach \x in {-6,-4,-2,0,2,4,6}
\foreach \y in {-6,-4,-2,0,2,4,6}{
\pgfmathparse{not(equal(\x,0))}
\ifnum\pgfmathresult=1
\pgfmathparse{\x>0}
\ifnum\pgfmathresult=1
\pgfmathsetmacro{\p}{atan(\y/\x)}
\else
\pgfmathsetmacro{\p}{atan(\y/\x)+180}
\fi
\pgfmathsetmacro{\t}{\k*\p+\c}
\draw[very thick] (\x,\y) +(\t:-0.9) -- +(\t:0.9);
\else
\pgfmathparse{not(equal(\y,0))}
\ifnum\pgfmathresult=1
\pgfmathparse{\y>0}
\ifnum\pgfmathresult=1
\pgfmathsetmacro{\p}{90}
\else
\pgfmathsetmacro{\p}{270}
\fi
\pgfmathsetmacro{\t}{\k*\p+\c}
\draw[very thick] (\x,\y) +(\t:-0.9) -- +(\t:0.9);
\fi
\fi}
}
繰り返し処理は具体的に次のように書きました.scope 環境の xshift, yshift を使って新しいトポロジカル欠陥をずらして表示しています.
\begin{tikzpicture}[scale=0.23]
\pgfmathsetmacro{\xshift}{450} %どれだけx方向にずらすか
\pgfmathsetmacro{\yshift}{-500} %どれだけy方向にずらすか
\pgfmathsetmacro{\X}{0}
\pgfmathsetmacro{\Y}{0}
\foreach \k/\c[remember=\X, remember=\Y] in %k,cを動かす
{1/0, 1/30, 1/60, 1/90,
-1/0, -1/30, -1/60, -1/90,
{1/2}/0, {-1/2}/0, 2/0, -2/0,
{3/2}/0, {-3/2}/0, 3/0, -3/0}{
\begin{scope}[xshift=\xshift*\X, yshift=\yshift*\Y]
\defect{\k}{\c} %描画
\end{scope}
\pgfmathparse{not(equal(\X,3))}
\ifnum \pgfmathresult=1 %X!=3
\pgfmathsetmacro{\X}{\X+1} %Xを1増やす
\else %X=3
\pgfmathsetmacro{\X}{0} %X=0にリセット
\pgfmathsetmacro{\Y}{\Y+1} %Yを1増やす
\fi
}
\end{tikzpicture}
ヨシ!
まとめ
今回はこけし,Barnsley fern,トポロジカル欠陥を TikZ と PGF を使って描きました.参考になったでしょうか.私もまだ勉強中の身なので,もっと良い方法があるかもしれません.またブラッシュアップしたものを公開したいです.
普段 TikZ を使っていて困ったときにはターミナルで texdoc visualtikz を叩いています.TikZ のマニュアルはクソデカということで有名ですが,こちらのマニュアルはよくまとまっていて見易いので重宝しています.それでも困ったときには仕方なく texdoc tikz を叩いています.(texdoc は実数さんに教えてもらった知見です.)
私は普段レポートの図や演習・ゼミの発表資料は TikZ で描いています.明らかに見易さが違うのでもっと褒めてほしいです.(たまに褒めてくれる先生がいます.褒められると懐きます.)
手書きの図で済ませてしまっても良いですが,教養としてこういう図が作れるようにしておくことは大切だと思います.いざというときに困ってしまいますからね.(論文に手書きの図を載せるような人間にはなりたくないです.)
良い TikZ ライフを!
参考文献
- 私
更新履歴
2021/12/12:\filldraw の説明なのに \fill と変わらない例になってしまっていたので,\filldraw[orange] を \filldraw[fill=orange] に変更して図を差し替えました.
2021/12/12:アフィン写像の $+\boldsymbol{v}_i$ の成分 $\boldsymbol{v}_i=(e_i,f_i)$ が写像 $f_i(\boldsymbol{x})$ のノーテーションとぶつかっていたので,成分を $\boldsymbol{v}_i=(v_i,u_i)$ に変更しました.
2021/12/13:軽微なタイポを修正.